Analytic element method on:
[Wikipedia]
[Google]
[Amazon]
The analytic element method (AEM) is a numerical method used for the solution of partial differential equations. It was initially developed by O.D.L. Strack at the 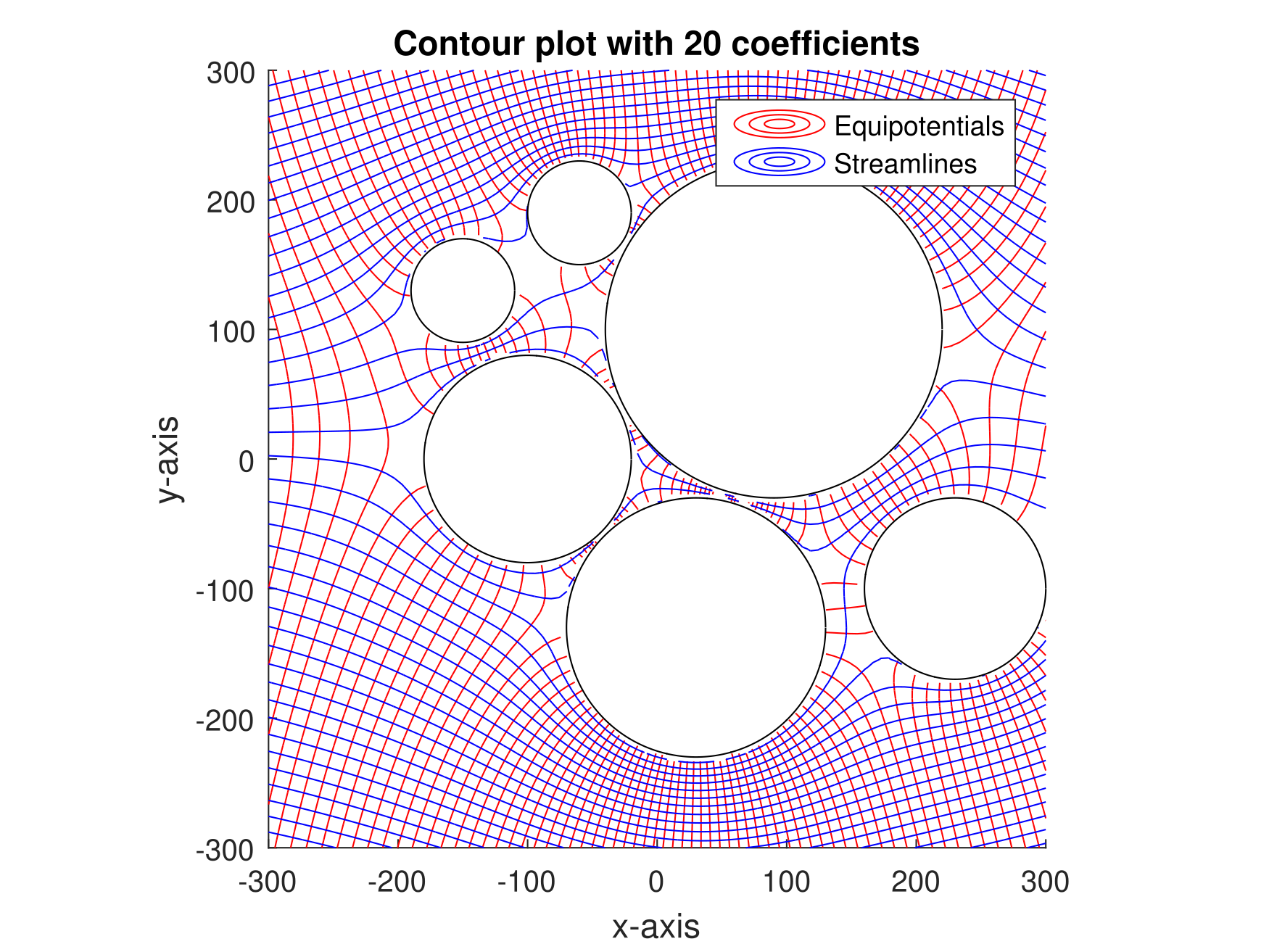
Analytic elements community wiki
Fitts Geolsolutions, AnAqSim (analytic aquifer simulator) and AnAqSimEDU (free) web site
{{DEFAULTSORT:Analytic Element Method Numerical differential equations Hydrology models
University of Minnesota
The University of Minnesota, formally the University of Minnesota, Twin Cities, (UMN Twin Cities, the U of M, or Minnesota) is a public land-grant research university in the Twin Cities of Minneapolis and Saint Paul, Minnesota, United States. ...
. It is similar in nature to the boundary element method
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations (i.e. in ''boundary integral'' form), including fluid mechanics, acoustics, el ...
(BEM), as it does not rely upon discretization of volumes or areas in the modeled system; only internal and external boundaries are discretized. One of the primary distinctions between AEM and BEMs is that the boundary integrals are calculated analytically.

Mathematical basis
The basic premise of the analytic element method is that, forlinear differential equation
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form
:a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b ...
s, elementary solutions may be superimposed to obtain more complex solutions. A suite of 2D and 3D analytic solutions ("elements") are available for different governing equations. These elements typically correspond to a discontinuity in the dependent variable or its gradient along a geometric boundary (e.g., point, line, ellipse, circle, sphere, etc.). This discontinuity has a specific functional form (usually a polynomial in 2D) and may be manipulated to satisfy Dirichlet, Neumann, or Robin (mixed) boundary conditions. Each analytic solution is infinite in space and/or time.
Commonly each analytic solution contains degrees of freedom (coefficients) that may be calculated to meet prescribed boundary conditions along the element's border. To obtain a global solution (i.e., the correct element coefficients), a system of equations is solved such that the boundary conditions are satisfied along all of the elements (using collocation, least-squares minimization, or a similar approach). Notably, the global solution provides a spatially continuous description of the dependent variable everywhere in the infinite domain, and the governing equation is satisfied everywhere exactly except along the border of the element, where the governing equation is not strictly applicable due to the discontinuity.
The ability to superpose numerous elements in a single solution means that analytical solutions can be realized for arbitrarily complex boundary conditions. That is, models that have complex geometries, straight or curved boundaries, multiple boundaries, transient boundary conditions, multiple aquifer layers, piecewise varying properties and continuously varying properties can be solved. Elements can be implemented using far-field expansions such that model containing many thousands of elements can be solved efficiently to high precision.
The analytic element method has been applied to problems of groundwater flow
Groundwater is the water present beneath Earth's surface in rock and soil pore spaces and in the fractures of rock formations. About 30 percent of all readily available freshwater in the world is groundwater. A unit of rock or an unconsolidate ...
governed by a variety of linear partial differential equations including the Laplace, the Poisson equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with t ...
, the modified Helmholtz equation, the heat equation, and the biharmonic
In mathematics, the biharmonic equation is a fourth-order partial differential equation which arises in areas of continuum mechanics, including linear elasticity theory and the solution of Stokes flows. Specifically, it is used in the modeling of ...
equations. Often theses equations are solved using complex variables which enables using mathematical techniques available in complex variable theory. A useful technique to solve complex problems is using conformal mapping which maps the boundary of a geometry, e.g. an ellipse, onto the boundary of the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
where the solution is known.
In the analytic element method the discharge potential and stream function
The stream function is defined for incompressible ( divergence-free) flows in two dimensions – as well as in three dimensions with axisymmetry. The flow velocity components can be expressed as the derivatives of the scalar stream function. T ...
, or combined the complex potential, is used. This potential links the physical properties of the groundwater system, the hydraulic head or flow boundaries, to a mathematical representation in a potential. This mathematical representation can be used to calculate the potential in terms of position and thus also solving groundwater flow problems. Elements are developed by solving the boundary conditions for either of these two properties, hydraulic head or flow boundary, which results in analytical solutions capable of dealing with numerous boundary conditions.
A contemporary student of Strack's who is a proponent of the Analytic Element Method (AEM) in groundwater modeling applications is Dr. David Steward of North Dakota State University.
Comparison to other methods
As mentioned the analytic element method thus not rely on discretization of volume or area in the model, as in the finite elements or finite different methods. Thus, it can model complex problem with an error on the order of machine precision. This is illustrated in a study which modeled a highly heterogeneous, isotropic aquifer by including 100,000 spherical heterogeneity with a random conductivity and tracing 40,000 particles. The analytical element method can efficiently be used as verification or as a screening tool in larger projects as it may fast and accurately calculate the groundwater flow for many complex problems. In contrast to other commonly used groundwater modeling methods, e.g. the finite elements or finite different method, the AEM does not discrete the model domain into cells. This gives the advantage that the model is valid for any given point in the model domain. However, it also imposes that the domain is not as easily divided into regions of e.g. different hydraulic conductivity, as when modeling with a cell grid. While there are some solutions that deals with this, e.g. there exist solutions for implementing a vertically varying properties or structures in an aquifer in an AEM model.See also
*Boundary element method
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations (i.e. in ''boundary integral'' form), including fluid mechanics, acoustics, el ...
* Conformal mapping
* Superposition principle
References
Further read
* * *External links
Analytic elements community wiki
Fitts Geolsolutions, AnAqSim (analytic aquifer simulator) and AnAqSimEDU (free) web site
{{DEFAULTSORT:Analytic Element Method Numerical differential equations Hydrology models