|
Spherical Wedge
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned ea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
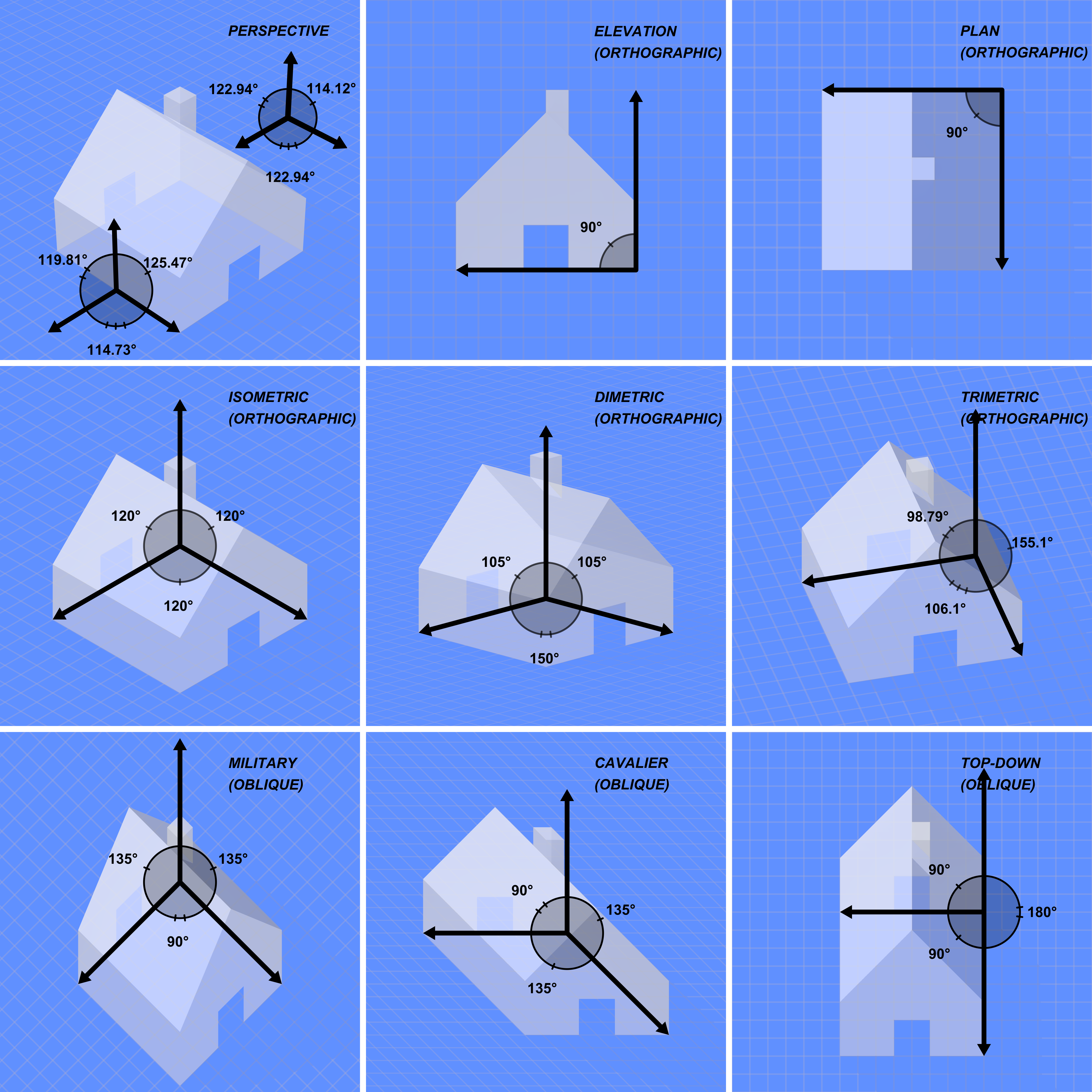
3D Projection
A 3D projection (or graphical projection) is a Design, design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on perspective (graphical), visual perspective and aspect analysis to Projection mapping, project a complex object for viewing capability on a simpler plane. 3D projections use the Primary Qualities, primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (such as paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, technical drawing, drafting, and computer graphics. Projections can be calculated through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spherical Earth
Spherical Earth or Earth's curvature refers to the approximation of the figure of the Earth as a sphere. The earliest documented mention of the concept dates from around the 5th century BC, when it appears in the writings of Ancient Greek philosophy, Greek philosophers. In the 3rd century BC, History of geodesy#Hellenic world, Hellenistic astronomy established the figure of the Earth, roughly spherical shape of Earth as a physical fact and calculated the Earth's circumference. This knowledge was gradually adopted throughout the Old World during late antiquity, Late Antiquity and the Middle Ages, displacing earlier beliefs in a flat earth.Adoption by China via European science: and A practical demonstration of Earth's sphericity was achieved by Ferdinand Magellan and Juan Sebastián Elcano's circumnavigation (1519–1522). The realization that the figure of the Earth is more accurately described as an Earth ellipsoid, ellipsoid dates to the 17th century, as described by Isa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Unit Sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -sphere of unit radius in -dimensional Euclidean space; the unit circle is a special case, the unit -sphere in the Euclidean plane, plane. An (Open set, open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center. A sphere or ball with unit radius and center at the origin (mathematics), origin of the space is called ''the'' unit sphere or ''the'' unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of translation (geometry), translation and scaling (geometry), scaling, so the study of spheres in general can often be reduced to the study of the unit sphere. The unit sphere is often used as a model for spherical geometry because it has constant sectional cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Antipodal Point
In mathematics, two points of a sphere (or n-sphere, including a circle) are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its center. Given any point on a sphere, its antipodal point is the unique point at greatest distance, whether measured intrinsically (great-circle distance on the surface of the sphere) or extrinsically ( chordal distance through the sphere's interior). Every great circle on a sphere passing through a point also passes through its antipodal point, and there are infinitely many great circles passing through a pair of antipodal points (unlike the situation for any non-antipodal pair of points, which have a unique great circle passing through both). Many results in spherical geometry depend on choosing non-antipodal points, and degenerate if antipodal points are allowed; for example, a spherical triangle degenerates to an underspecified lune if t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sphere And Ball
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ball Bearings
A ball bearing is a type of rolling-element bearing that uses balls to maintain the separation between the bearing races. The purpose of a ball bearing is to reduce rotational friction and support radial and axial loads. It achieves this by using at least two races to contain the balls and transmit the loads through the balls. In most applications, one race is stationary and the other is attached to the rotating assembly (e.g., a hub or shaft). As one of the bearing races rotates it causes the balls to rotate as well. Because the balls are rolling, they have a much lower coefficient of friction than if two flat surfaces were sliding against each other. Ball bearings tend to have lower load capacity for their size than other kinds of rolling-element bearings due to the smaller contact area between the balls and races. However, they can tolerate some misalignment of the inner and outer races. Common ball bearing designs include ''angular contact, axial, deep-groove,'' a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ball
A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for simpler activities, such as catch or juggling. Balls made from hard-wearing materials are used in engineering applications to provide very low friction bearings, known as ball bearings. Black-powder weapons use stone and metal balls as projectiles. Although many types of balls are today made from rubber, this form was unknown outside the Americas until after the voyages of Columbus. The Spanish were the first Europeans to see the bouncing rubber balls (although solid and not inflated) which were employed most notably in the Mesoamerican ballgame. Balls used in various sports in other parts of the world prior to Columbus were made from other materials such as animal bladders or skins, stuffed with various materials. As balls are one of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rolling
Rolling is a Motion (physics)#Types of motion, type of motion that combines rotation (commonly, of an Axial symmetry, axially symmetric object) and Translation (geometry), translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding (motion), sliding. Rolling where there is no sliding is referred to as ''pure rolling''. By definition, there is no sliding when there is a frame of reference in which all points of contact on the rolling object have the same velocity as their counterparts on the surface on which the object rolls; in particular, for a frame of reference in which the rolling plane is at rest (see animation), the instantaneous velocity of all the points of contact (for instance, a generating line segment of a cylinder) of the rolling object is zero. In practice, due to small deformations near the contact area, some sliding and energy dissipation occurs. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lens
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements''), usually arranged along a common axis. Lenses are made from materials such as glass or plastic and are ground, polished, or molded to the required shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called "lenses", such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses. Lenses are used in various imaging devices such as telescopes, binoculars, and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia. History The word '' lens'' comes from , the Latin name of the lentil (a seed of a lentil p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Curved Mirror
A curved mirror is a mirror with a curved reflecting surface. The surface may be either ''convex'' (bulging outward) or ''concave'' (recessed inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors, found in optical devices such as reflecting telescopes that need to image distant objects, since spherical mirror systems, like spherical lenses, suffer from spherical aberration. Distorting mirrors are used for entertainment. They have convex and concave regions that produce deliberately distorted images. They also provide highly magnified or highly diminished (smaller) images when the object is placed at certain distances. Convex mirrors are often used for security and safety in shops and parking lots. Convex mirrors A convex mirror or diverging mirror is a curved mirror in which the reflective surface bulges towards the light source. Con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pressure Vessels
A pressure vessel is a container designed to hold gases or liquids at a pressure substantially different from the ambient pressure. Construction methods and materials may be chosen to suit the pressure application, and will depend on the size of the vessel, the contents, working pressure, mass constraints, and the number of items required. Pressure vessels can be dangerous, and fatal accidents have occurred in the history of their development and operation. Consequently, pressure vessel design, manufacture, and operation are regulated by engineering authorities backed by legislation. For these reasons, the definition of a pressure vessel varies from country to country. The design involves parameters such as maximum safe operating pressure and temperature, safety factor, corrosion allowance and minimum design temperature (for brittle fracture). Construction is tested using nondestructive testing, such as ultrasonic testing, radiography, and pressure tests. Hydrostatic pressure t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |