|
Principal Ideal Domain
In mathematics, a principal ideal domain, or PID, is an integral domain (that is, a non-zero commutative ring without nonzero zero divisors) in which every ideal is principal (that is, is formed by the multiples of a single element). Some authors such as Bourbaki refer to PIDs as principal rings. Principal ideal domains are mathematical objects that behave like the integers, with respect to divisibility: any element of a PID has a unique factorization into prime elements (so an analogue of the fundamental theorem of arithmetic holds); any two elements of a PID have a greatest common divisor (although it may not be possible to find it using the Euclidean algorithm). If and are elements of a PID without common divisors, then every element of the PID can be written in the form , etc. Principal ideal domains are Noetherian, they are integrally closed, they are unique factorization domains and Dedekind domains. All Euclidean domains and all fields are principal ideal domain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euclidean Domain
In mathematics, more specifically in ring theory, a Euclidean domain (also called a Euclidean ring) is an integral domain that can be endowed with a Euclidean function which allows a suitable generalization of Euclidean division of integers. This generalized Euclidean algorithm can be put to many of the same uses as Euclid's original algorithm in the ring of integers: in any Euclidean domain, one can apply the Euclidean algorithm to compute the greatest common divisor of any two elements. In particular, the greatest common divisor of any two elements exists and can be written as a linear combination of them ( Bézout's identity). In particular, the existence of efficient algorithms for Euclidean division of integers and of polynomials in one variable over a field is of basic importance in computer algebra. It is important to compare the class of Euclidean domains with the larger class of principal ideal domains (PIDs). An arbitrary PID has much the same "structural proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Unique Factorization
In mathematics, a unique factorization domain (UFD) (also sometimes called a factorial ring following the terminology of Bourbaki) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain (a nontrivial commutative ring in which the product of any two non-zero elements is non-zero) in which every non-zero non- unit element can be written as a product of irreducible elements, uniquely up to order and units. Important examples of UFDs are the integers and polynomial rings in one or more variables with coefficients coming from the integers or from a field. Unique factorization domains appear in the following chain of class inclusions: Definition Formally, a unique factorization domain is defined to be an integral domain ''R'' in which every non-zero element ''x'' of ''R'' which is not a unit can be written as a finite product of irreducible elements ''p''''i'' of ''R'': : ''x'' = ''p''1 ''p''2 ⋅⋅� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ring Of Algebraic Integers
In algebraic number theory, an algebraic integer is a complex number that is integral over the integers. That is, an algebraic integer is a complex root of some monic polynomial (a polynomial whose leading coefficient is 1) whose coefficients are integers. The set of all algebraic integers is closed under addition, subtraction and multiplication and therefore is a commutative subring of the complex numbers. The ring of integers of a number field , denoted by , is the intersection of and : it can also be characterized as the maximal order of the field . Each algebraic integer belongs to the ring of integers of some number field. A number is an algebraic integer if and only if the ring \mathbbalpha/math> is finitely generated as an abelian group, which is to say, as a \mathbb- module. Definitions The following are equivalent definitions of an algebraic integer. Let be a number field (i.e., a finite extension of \mathbb, the field of rational numbers), in other words, K = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polynomial Ring
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates (traditionally also called variables) with coefficients in another ring, often a field. Often, the term "polynomial ring" refers implicitly to the special case of a polynomial ring in one indeterminate over a field. The importance of such polynomial rings relies on the high number of properties that they have in common with the ring of the integers. Polynomial rings occur and are often fundamental in many parts of mathematics such as number theory, commutative algebra, and algebraic geometry. In ring theory, many classes of rings, such as unique factorization domains, regular rings, group rings, rings of formal power series, Ore polynomials, graded rings, have been introduced for generalizing some properties of polynomial rings. A closely related notion is that of the ring of polynomial functions on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
P-adic Integer
In number theory, given a prime number , the -adic numbers form an extension of the rational numbers which is distinct from the real numbers, though with some similar properties; -adic numbers can be written in a form similar to (possibly infinity (mathematics), infinite) decimal representation, decimals, but with digits based on a prime number rather than ten, and extending to the left rather than to the right. For example, comparing the expansion of the rational number \tfrac15 in Ternary numeral system, base vs. the -adic expansion, \begin \tfrac15 &= 0.01210121\ldots \ (\text 3) &&= 0\cdot 3^0 + 0\cdot 3^ + 1\cdot 3^ + 2\cdot 3^ + \cdots \\[5mu] \tfrac15 &= \dots 121012102 \ \ (\text) &&= \cdots + 2\cdot 3^3 + 1 \cdot 3^2 + 0\cdot3^1 + 2 \cdot 3^0. \end Formally, given a prime number , a -adic number can be defined as a series (mathematics), series s=\sum_^\infty a_i p^i = a_k p^k + a_ p^ + a_ p^ + \cdots where is an integer (possibly negative), and each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Valuation Ring
In abstract algebra, a discrete valuation ring (DVR) is a principal ideal domain (PID) with exactly one non-zero maximal ideal. This means a DVR is an integral domain ''R'' that satisfies any and all of the following equivalent conditions: # ''R'' is a local ring, a principal ideal domain, and not a field. # ''R'' is a valuation ring with a value group isomorphic to the integers under addition. # ''R'' is a local ring, a Dedekind domain, and not a field. # ''R'' is Noetherian and a local domain whose unique maximal ideal is principal, and not a field. # ''R'' is integrally closed, Noetherian, and a local ring with Krull dimension one. # ''R'' is a principal ideal domain with a unique non-zero prime ideal. # ''R'' is a principal ideal domain with a unique irreducible element (up to multiplication by units). # ''R'' is a unique factorization domain with a unique irreducible element (up to multiplication by units). # ''R'' is Noetherian, not a field, and every nonzero fraction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
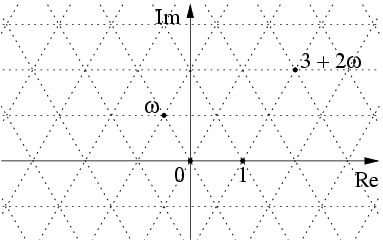
Eisenstein Integers
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by : (a + b\;\!\omega) \; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cube Root
In mathematics, a cube root of a number is a number that has the given number as its third power; that is y^3=x. The number of cube roots of a number depends on the number system that is considered. Every real number has exactly one real cube root that is denoted \sqrt /math> and called the ''real cube root'' of or simply ''the cube root'' of in contexts where complex numbers are not considered. For example, the real cube roots of and are respectively and . The real cube root of an integer or of a rational number is generally not a rational number, neither a constructible number. Every nonzero real or complex number has exactly three cube roots that are complex numbers. If the number is real, one of the cube roots is real and the two other are nonreal complex conjugate numbers. Otherwise, the three cube roots are all nonreal. For example, the real cube root of is and the other cube roots of are -1+i\sqrt 3 and -1-i\sqrt 3. The three cube roots of are 3i, \tfrac-\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gaussian Integers
In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as \mathbf /math> or \Z Gaussian integers share many properties with integers: they form a Euclidean domain, and thus have a Euclidean division and a Euclidean algorithm; this implies unique factorization and many related properties. However, Gaussian integers do not have a total order that respects arithmetic. Gaussian integers are algebraic integers and form the simplest ring of quadratic integers. Gaussian integers are named after the German mathematician Carl Friedrich Gauss. Basic definitions The Gaussian integers are the set :\mathbf \, \qquad \text i^2 = -1. In other words, a Gaussian integer is a complex number such that its real and imaginary parts are both integers. Since the Gaussian integers are closed under addition and multipli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ring Of Formal Power Series
In mathematics, a formal series is an infinite sum that is considered independently from any notion of convergence, and can be manipulated with the usual algebraic operations on series (addition, subtraction, multiplication, division, partial sums, etc.). A formal power series is a special kind of formal series, of the form \sum_^\infty a_nx^n=a_0+a_1x+ a_2x^2+\cdots, where the a_n, called ''coefficients'', are numbers or, more generally, elements of some ring, and the x^n are formal powers of the symbol x that is called an indeterminate or, commonly, a variable. Hence, power series can be viewed as a generalization of polynomials where the number of terms is allowed to be infinite, and differ from usual power series by the absence of convergence requirements, which implies that a power series may not represent a function of its variable. Formal power series are in one to one correspondence with their sequences of coefficients, but the two concepts must not be confused, since th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polynomial Ring
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates (traditionally also called variables) with coefficients in another ring, often a field. Often, the term "polynomial ring" refers implicitly to the special case of a polynomial ring in one indeterminate over a field. The importance of such polynomial rings relies on the high number of properties that they have in common with the ring of the integers. Polynomial rings occur and are often fundamental in many parts of mathematics such as number theory, commutative algebra, and algebraic geometry. In ring theory, many classes of rings, such as unique factorization domains, regular rings, group rings, rings of formal power series, Ore polynomials, graded rings, have been introduced for generalizing some properties of polynomial rings. A closely related notion is that of the ring of polynomial functions on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |