|
Curve Fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference such as how much uncertainty is present in a curve that is fitted to data observed with random errors. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables. Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data. For linear-algebraic ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
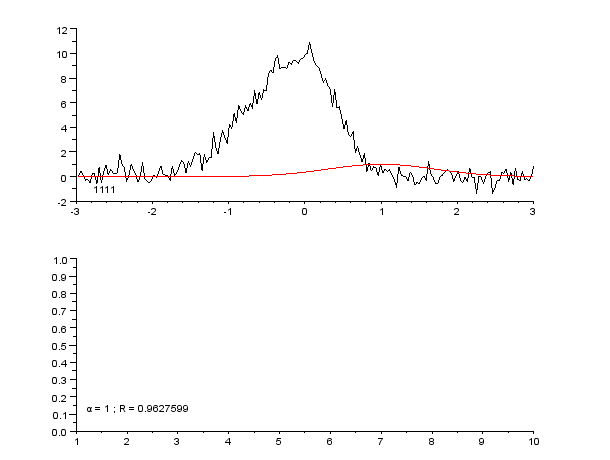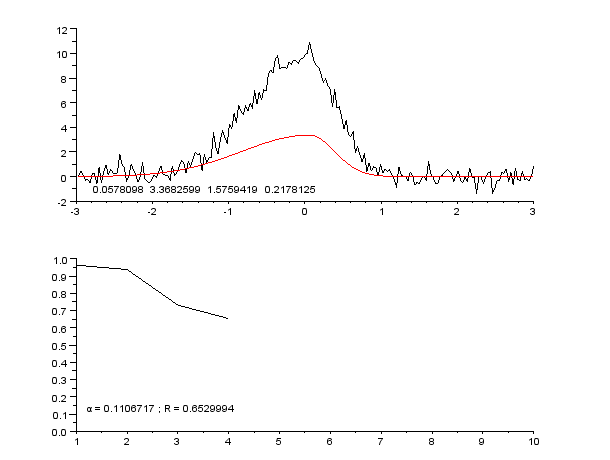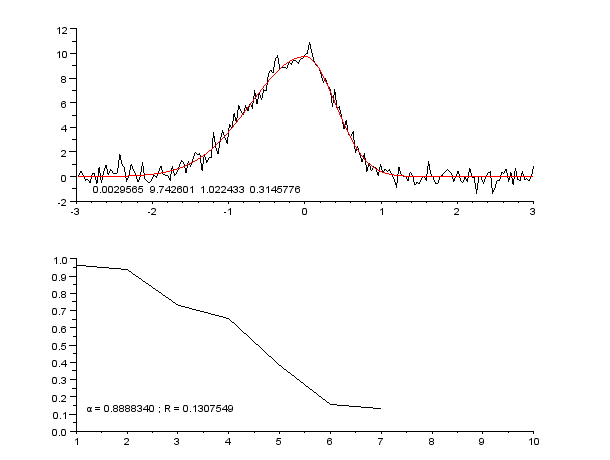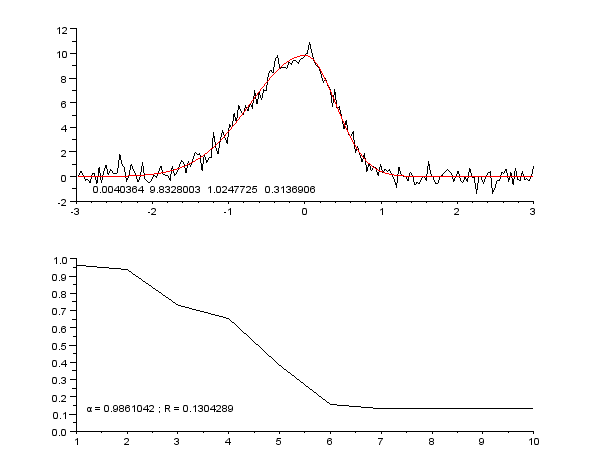
Regression Pic Assymetrique
Regression or regressions may refer to: Arts and entertainment * ''Regression'' (film), a 2015 horror film by Alejandro Amenábar, starring Ethan Hawke and Emma Watson * ''Regression'' (magazine), an Australian punk rock fanzine (1982–1984) * ''Regressions'' (album), 2010 album by Cleric Computing * Software regression, the appearance of a bug in functionality that was working correctly in a previous revision ** Regression testing, a software testing method which seeks to uncover regression bugs Hypnosis * Age regression in therapy, a process claiming to retrieve memories * Past life regression, a process claiming to retrieve memories of previous lives Science * Marine regression, coastal advance due to falling sea level, the opposite of marine transgression * Regression (medicine), a characteristic of diseases to express lighter symptoms or less extent (mainly for tumors), without disappearing totally * Regression (psychology), a defensive reaction to some unaccepted i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Slope
In mathematics, the slope or gradient of a Line (mathematics), line is a number that describes the direction (geometry), direction of the line on a plane (geometry), plane. Often denoted by the letter ''m'', slope is calculated as the ratio of the vertical change to the horizontal change ("rise over run") between two distinct points on the line, giving the same number for any choice of points. The line may be physical – as set by a Surveying, road surveyor, pictorial as in a diagram of a road or roof, or Pure mathematics, abstract. An application of the mathematical concept is found in the grade (slope), grade or gradient in geography and civil engineering. The ''steepness'', incline, or grade of a line is the absolute value of its slope: greater absolute value indicates a steeper line. The line trend is defined as follows: *An "increasing" or "ascending" line goes from left to right and has positive slope: m>0. *A "decreasing" or "descending" line goes from left to right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their multiplicative inverse, reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding Inverse trigonometric functions, inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gohana Inverted S-curve
Gohana is a city and a municipal council, near Sonipat city in the Sonipat district of the Indian state of Haryana. Gohana is the oldest Tehsil of Haryana. Gohana is also famous all over the world for its Maturam's Jalebi (which is also national sweet of India). Geography Gohana is located at . Its topography consists mainly of low plains, but its south-central area has a small plateau. Gohana's 43 km2 (27.95sq mile) land area has an average elevation of 225 metres (738 feet). Demographics Gohana city is situated in the Sonipat district of Haryana. It is the main subdivision with a population of more than 300,000 (as of 2011). It has its own municipality and a constituency for Haryana Vidhan Sabha. There are around 86 Villages in Gohana. It is located in the west of the Sonipat District, 40 km from the town of Sonipat. Earlier, it was part of Rohtak district. Gohana is the oldest tehsil of Haryana. It was declared a tehsil in 1826 by the British, and som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Inflection Point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (rarely inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa. For the graph of a function of differentiability class (its first derivative , and its second derivative , exist and are continuous), the condition can also be used to find an inflection point since a point of must be passed to change from a positive value (concave upward) to a negative value (concave downward) or vice versa as is continuous; an inflection point of the curve is where and changes its sign at the point (from positive to negative or from negative to positive). A point where the second derivative vanishes but does not change its sign is sometimes called a point of undulation or und ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Magnitude (mathematics)
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an ordering (or ranking) of the class of objects to which it belongs. Magnitude as a concept dates to Ancient Greece and has been applied as a measure of distance from one object to another. For numbers, the absolute value of a number is commonly applied as the measure of units between a number and zero. In vector spaces, the Euclidean norm is a measure of magnitude used to define a distance between two points in space. In physics, magnitude can be defined as quantity or distance. An order of magnitude is typically defined as a unit of distance between one number and another's numerical places on the decimal scale. History Ancient Greeks distinguished between several types of magnitude, including: * Positive fractions * Line segments (orde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Runge's Phenomenon
In the mathematical field of numerical analysis, Runge's phenomenon () is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree over a set of equispaced interpolation points. It was discovered by Carl David Tolmé Runge (1901) when exploring the behavior of errors when using polynomial interpolation to approximate certain functions. The discovery shows that going to higher degrees does not always improve accuracy. The phenomenon is similar to the Gibbs phenomenon in Fourier series approximations. The Weierstrass approximation theorem states that for every continuous function f(x) defined on an interval , b/math>, there exists a set of polynomial functions P_n(x) for n=0, 1, 2, \ldots, each of degree at most n, that approximates f(x) with uniform convergence over , b/math> as n tends to infinity. This can be expressed as: :\lim_ \left( \sup_ \left, f(x) - P_n(x) \ \right) = 0. Consider the case w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Collinear Points
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row". Points on a line In any geometry, the set of points on a line are said to be collinear. In Euclidean geometry this relation is intuitively visualized by points lying in a row on a "straight line". However, in most geometries (including Euclidean) a line is typically a primitive (undefined) object type, so such visualizations will not necessarily be appropriate. A model for the geometry offers an interpretation of how the points, lines and other object types relate to one another and a notion such as collinearity must be interpreted within the context of that model. For instance, in spherical geometry, where lines are represented in the standard model by great circles of a spher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jerk (physics)
Jerk (also known as jolt) is the rate of change of an object's acceleration over time. It is a vector quantity (having both magnitude and direction). Jerk is most commonly denoted by the symbol and expressed in m/s3 (SI units) or standard gravities per second(''g''0/s). Expressions As a vector, jerk can be expressed as the first time derivative of acceleration, second time derivative of velocity, and third time derivative of position: \mathbf j(t) = \frac = \frac = \frac Where: * is acceleration * is velocity * is position * is time. Third-order differential equations of the form J\left(\overset, \ddot, \dot, x\right) = 0 are sometimes called ''jerk equations''. When converted to an equivalent system of three ordinary first-order non-linear differential equations, jerk equations are the minimal setting for solutions showing chaotic behaviour. This condition generates mathematical interest in ''jerk systems''. Systems involving fourth-order derivatives or higher are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cloverleaf Interchange
A cloverleaf interchange is a two-level interchange (road), interchange in which all turns are handled by slip roads. To go left (in right-hand traffic; reverse directions in left-driving regions), vehicles first continue as one road passes over or under the other, then exit right onto a one-way three-quarter loop ramp (270°) and merge onto the intersecting road. The objective of a cloverleaf is to allow two highways to cross without the need for any traffic to be stopped by traffic lights. The limiting factor in the capacity of a cloverleaf interchange is traffic weaving. Overview Cloverleaf interchanges, viewed from overhead or on maps, resemble the leaf, leaves of a four-leaf clover or less often a 3-leaf clover. In the United States, cloverleaf interchanges existed long before the Interstate highway, Interstate system. They were originally created for busier interchanges that the original diamond interchange system could not handle. Their chief advantage was that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spline (mathematics)
In mathematics, a spline is a function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees. In the computer science subfields of computer-aided design and computer graphics, the term ''spline'' more frequently refers to a piecewise polynomial ( parametric) curve. Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design. The term spline comes from the flexible spline devices used by shipbuilders and draftsmen to draw smooth shapes. Introduction The term "spline" is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. The data ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |