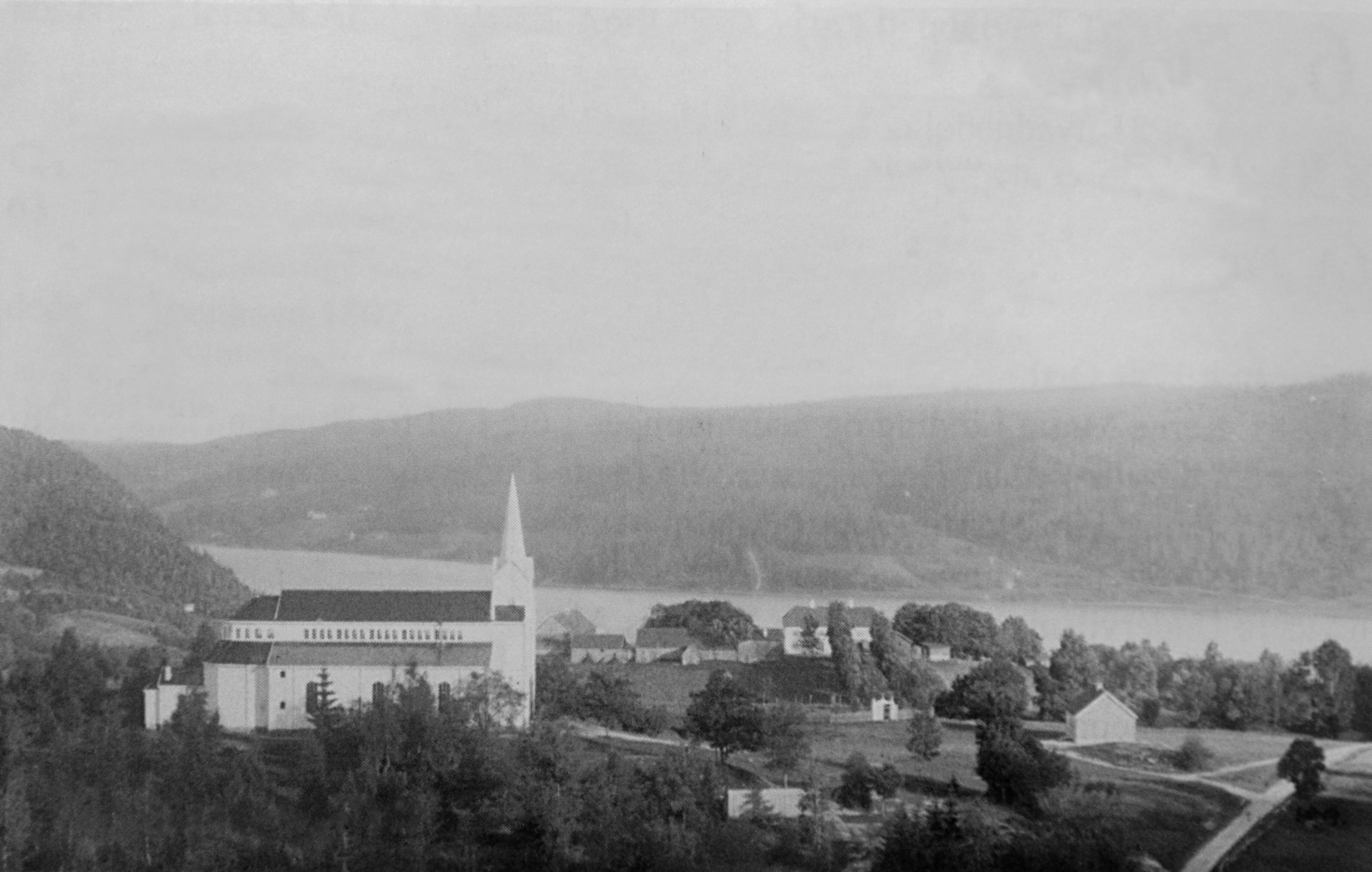|
Niels Henrik Abel
Niels Henrik Abel ( , ; 5 August 1802 – 6 April 1829) was a Norwegian mathematician who made pioneering contributions in a variety of fields. His most famous single result is the first complete proof demonstrating the impossibility of solving the general quintic equation in radicals. This question was one of the outstanding open problems of his day, and had been unresolved for over 250 years. He was also an innovator in the field of elliptic functions, discoverer of Abelian functions. He made his discoveries while living in poverty and died at the age of 26 from tuberculosis. Most of his work was done in six or seven years of his working life. Regarding Abel, the French mathematician Charles Hermite said: "Abel has left mathematicians enough to keep them busy for five hundred years." Another French mathematician, Adrien-Marie Legendre, said: "What a head the young Norwegian has!" The Abel Prize in mathematics, originally proposed in 1899 to complement the Nobel Prizes (but f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nedstrand
Nedstrand (locally, ''Stranda'') is a village in Tysvær municipality in Rogaland county, Norway. The village is on the Nedstrand peninsula's southeast coast, at the confluence of the Nedstrandsfjorden and Vindafjorden. The village of Hindaråvåg lies just west of Nedstrand, and Nedstrand Church is there. The village has a population (2019) of 227 and a population density of . The village is a regular ferry stop on routes to the Sjernarøyane islands (across the Nedstrandsfjorden) and to Hebnes (across the Vindafjorden). Both of those stops have other connections all over the region. The area was historically part of the municipality of Nedstrand, and was a regional customs office for the huge timber industry in the Ryfylke district. Today, the area is home to agriculture, fish farming, fruit orchards, and stone quarries. In 1983, the oil rig Alexander L. Kielland was scuttled in the Nedstrandsfjorden after it had capsized in the North Sea in 1980, killing 123 people. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abel–Plana Formula
In mathematics, the Abel–Plana formula is a summation formula discovered independently by and . It states that :\sum_^\infty f(n)=\frac 1 2 f(0)+ \int_0^\infty f(x) \, dx+ i \int_0^\infty \frac \, dt. It holds for functions ''f'' that are holomorphic in the region Re(''z'') ≥ 0, and satisfy a suitable growth condition in this region; for example it is enough to assume that , ''f'', is bounded by ''C''/, ''z'', 1+ε in this region for some constants ''C'', ε > 0, though the formula also holds under much weaker bounds. . An example is provided by the Hurwitz zeta function, :\zeta(s,\alpha)= \sum_^\infty \frac = \frac + \frac 1 + 2\int_0^\infty\frac\frac, which holds for all s \in \mathbb, . Abel also gave the following variation for alternating sums: :\sum_^\infty (-1)^nf(n)= \frac f(0)+i \int_0^\infty \frac \, dt. Which is related to the Lindelöf summation formula \sum_^(-1)^kf(k)=(-1)^m\int_^f(m-1/2+ix)\frac Proof Let f be holomorphic on \Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Quintic Equation
In algebra, a quintic function is a function of the form :g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\, where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a quintic function is defined by a polynomial of degree five. Because they have an odd degree, normal quintic functions appear similar to normal cubic functions when graphed, except they may possess one additional local maximum and one additional local minimum. The derivative of a quintic function is a quartic function. Setting and assuming produces a quintic equation of the form: :ax^5+bx^4+cx^3+dx^2+ex+f=0.\, Solving quintic equations in terms of radicals (''n''th roots) was a major problem in algebra from the 16th century, when cubic and quartic equations were solved, until the first half of the 19th century, when the impossibility of such a general solution was proved with the Abel–Ruffini theorem. Finding roots of a quintic equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians were Thales of Miletus (c. 624–c.546 BC); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. The number of known mathematicians grew when Pythagoras of Samos (c. 582–c. 507 BC) established the Pythagoreans, Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Abelian Variety
In mathematics, a dual abelian variety can be defined from an abelian variety ''A'', defined over a field ''K''. Definition To an abelian variety ''A'' over a field ''k'', one associates a dual abelian variety ''A''v (over the same field), which is the solution to the following moduli problem. A family of degree 0 line bundles parametrized by a ''k''-variety ''T'' is defined to be a line bundle ''L'' on ''A''×''T'' such that # for all t \in T, the restriction of ''L'' to ''A''× is a degree 0 line bundle, # the restriction of ''L'' to ×''T'' is a trivial line bundle (here 0 is the identity of ''A''). Then there is a variety ''A''v and a line bundle P \to A \times A^\vee,, called the Poincaré bundle, which is a family of degree 0 line bundles parametrized by ''A''v in the sense of the above definition. Moreover, this family is universal, that is, to any family ''L'' parametrized by ''T'' is associated a unique morphism ''f'': ''T'' → ''A''v so that ''L'' is isomorphic to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Variety Of CM-type
In mathematics, an abelian variety ''A'' defined over a field ''K'' is said to have CM-type if it has a large enough commutative subring in its endomorphism ring End(''A''). The terminology here is from complex multiplication theory, which was developed for elliptic curves in the nineteenth century. One of the major achievements in algebraic number theory and algebraic geometry of the twentieth century was to find the correct formulations of the corresponding theory for abelian varieties of dimension ''d'' > 1. The problem is at a deeper level of abstraction, because it is much harder to manipulate analytic functions of several complex variables. The formal definition is that : \operatorname_\mathbb(A) the tensor product of End(''A'') with the rational number field Q, should contain a commutative subring of dimension 2''d'' over Q. When ''d'' = 1 this can only be a quadratic field, and one recovers the cases where End(''A'') is an order in an imaginary quadratic field. For '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Variety
In mathematics, particularly in algebraic geometry, complex analysis and algebraic number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions. Abelian varieties are at the same time among the most studied objects in algebraic geometry and indispensable tools for much research on other topics in algebraic geometry and number theory. An abelian variety can be defined by equations having coefficients in any field; the variety is then said to be defined ''over'' that field. Historically the first abelian varieties to be studied were those defined over the field of complex numbers. Such abelian varieties turn out to be exactly those complex tori that can be embedded into a complex projective space. Abelian varieties defined over algebraic number fields are a special case, which is important also from the viewpoint of number theory. Localization techniques lead naturally fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abel Transformation
In mathematics, summation by parts transforms the summation of products of sequences into other summations, often simplifying the computation or (especially) estimation of certain types of sums. It is also called Abel's lemma or Abel transformation, named after Niels Henrik Abel who introduced it in 1826. Statement Suppose \ and \ are two sequences. Then, :\sum_^n f_k(g_-g_k) = \left(f_g_ - f_m g_m\right) - \sum_^n g_(f_- f_). Using the forward difference operator \Delta, it can be stated more succinctly as :\sum_^n f_k\Delta g_k = \left(f_ g_ - f_m g_m\right) - \sum_^ g_\Delta f_k, Summation by parts is an analogue to integration by parts: :\int f\,dg = f g - \int g\,df, or to Abel's summation formula: :\sum_^n f(k)(g_-g_)= \left(f(n)g_ - f(m) g_m\right) - \int_^n g_ f'(t) dt. An alternative statement is :f_n g_n - f_m g_m = \sum_^ f_k\Delta g_k + \sum_^ g_k\Delta f_k + \sum_^ \Delta f_k \Delta g_k which is analogous to the integration by parts formula for semimartingales. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abel Transform
In mathematics, the Abel transform,N. H. Abel, Journal für die reine und angewandte Mathematik, 1, pp. 153–157 (1826). named for Niels Henrik Abel, is an integral transform often used in the analysis of spherically symmetric or axially symmetric functions. The Abel transform of a function ''f''(''r'') is given by : F(y) = 2 \int_y^\infty \frac \,dr. Assuming that ''f''(''r'') drops to zero more quickly than 1/''r'', the inverse Abel transform is given by : f(r) = -\frac \int_r^\infty \frac \,\frac. In image analysis, the forward Abel transform is used to project an optically thin, axially symmetric emission function onto a plane, and the inverse Abel transform is used to calculate the emission function given a projection (i.e. a scan or a photograph) of that emission function. In absorption spectroscopy of cylindrical flames or plumes, the forward Abel transform is the integrated absorbance along a ray with closest distance ''y'' from the center of the flame, while the inve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abel's Theorem
In mathematics, Abel's theorem for power series relates a limit of a power series to the sum of its coefficients. It is named after Norwegian mathematician Niels Henrik Abel. Theorem Let the Taylor series G (x) = \sum_^\infty a_k x^k be a power series with real coefficients a_k with radius of convergence 1. Suppose that the series \sum_^\infty a_k converges. Then G(x) is continuous from the left at x = 1, that is, \lim_ G(x) = \sum_^\infty a_k. The same theorem holds for complex power series G(z) = \sum_^\infty a_k z^k, provided that z \to 1 entirely within a single ''Stolz sector'', that is, a region of the open unit disk where , 1-z, \leq M(1-, z, ) for some fixed finite M > 1. Without this restriction, the limit may fail to exist: for example, the power series \sum_ \frac n converges to 0 at z = 1, but is unbounded near any point of the form e^, so the value at z = 1 is not the limit as z tends to 1 in the whole open disk. Note that G(z) is continuous on the real cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abel's Test
In mathematics, Abel's test (also known as Abel's criterion) is a method of testing for the convergence of an infinite series. The test is named after mathematician Niels Henrik Abel. There are two slightly different versions of Abel's test – one is used with series of real numbers, and the other is used with power series in complex analysis. Abel's uniform convergence test is a criterion for the uniform convergence of a series of functions dependent on parameters. Abel's test in real analysis Suppose the following statements are true: # \sum a_n is a convergent series, # is a monotone sequence, and # is bounded. Then \sum a_nb_n is also convergent. It is important to understand that this test is mainly pertinent and useful in the context of non absolutely convergent series \sum a_n. For absolutely convergent series, this theorem, albeit true, is almost self evident. This theorem can be proved directly using summation by parts. Abel's test in complex analys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian And Tauberian Theorems
In mathematics, Abelian and Tauberian theorems are theorems giving conditions for two methods of summing divergent series to give the same result, named after Niels Henrik Abel and Alfred Tauber. The original examples are Abel's theorem showing that if a series converges to some limit then its Abel sum is the same limit, and Tauber's theorem showing that if the Abel sum of a series exists and the coefficients are sufficiently small (o(1/''n'')) then the series converges to the Abel sum. More general Abelian and Tauberian theorems give similar results for more general summation methods. There is not yet a clear distinction between Abelian and Tauberian theorems, and no generally accepted definition of what these terms mean. Often, a theorem is called "Abelian" if it shows that some summation method gives the usual sum for convergent series, and is called "Tauberian" if it gives conditions for a series summable by some method that allows it to be summable in the usual sense. In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |