|
Negative Zero
Signed zero is zero with an associated sign. In ordinary arithmetic, the number 0 does not have a sign, so that −0, +0 and 0 are equivalent. However, in computing, some number representations allow for the existence of two zeros, often denoted by −0 (negative zero) and +0 (positive zero), regarded as equal by the numerical comparison operations but with possible different behaviors in particular operations. This occurs in the ''sign-magnitude'' and ''ones' complement'' signed number representations for integers, and in most floating-point number representations. The number 0 is usually encoded as +0, but can still be represented by +0, −0, or 0. The IEEE 754 standard for floating-point arithmetic (presently used by most computers and programming languages that support floating-point numbers) requires both +0 and −0. Real arithmetic with signed zeros can be considered a variant of the extended real number line such that = −∞ and = +∞; division is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Zero
0 (zero) is a number representing an empty quantity. Adding (or subtracting) 0 to any number leaves that number unchanged; in mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures. Multiplying any number by 0 results in 0, and consequently division by zero has no meaning in arithmetic. As a numerical digit, 0 plays a crucial role in decimal notation: it indicates that the power of ten corresponding to the place containing a 0 does not contribute to the total. For example, "205" in decimal means two hundreds, no tens, and five ones. The same principle applies in place-value notations that uses a base other than ten, such as binary and hexadecimal. The modern use of 0 in this manner derives from Indian mathematics that was transmitted to Europe via medieval Islamic mathematicians and popularized by Fibonacci. It was independently used by the Maya. Common name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Two's Complement
Two's complement is the most common method of representing signed (positive, negative, and zero) integers on computers, and more generally, fixed point binary values. Two's complement uses the binary digit with the ''greatest'' value as the ''sign'' to indicate whether the binary number is positive or negative; when the most significant bit is ''1'' the number is signed as negative and when the most significant bit is ''0'' the number is signed as positive. As a result, non-negative numbers are represented as themselves: 6 is 0110, zero is 0000, and −6 is 1010 (the result of applying the bitwise NOT operator to 6 and adding 1). However, while the number of binary bits is fixed throughout a computation it is otherwise arbitrary. Unlike the ones' complement scheme, the two's complement scheme has only one representation for zero. Furthermore, arithmetic implementations can be used on signed as well as unsigned integers and differ only in the integer overflow situations. Proce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wrapper Class
In object-oriented programming, a wrapper class is a class that encapsulates types, so that those types can be used to create object instances and methods in another class that needs those types. So a primitive wrapper class is a wrapper class that encapsulates, hides or ''wraps'' data types from the eight primitive data types, so that these can be used to create instantiated objects with methods in another class or in other classes.J. Murach, ''Murach's Java Programming'', 4th Edition, Mike Murach and Associates, Inc., 2011. The primitive wrapper classes are found in the Java API. Primitive wrapper classes are used to create an that needs to represent primitive types in classes (i.e., in the Java API), in the package and in the reflection package. Collection classes are Java API-defined classes that can store objects in a manner similar to how data structures like arrays store primitive data types like int, double, long or char, etc., but arrays store primitive data types ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cast (computer Programming)
In computer science, type conversion, type casting, type coercion, and type juggling are different ways of changing an expression from one data type to another. An example would be the conversion of an integer value into a floating point value or its textual representation as a string, and vice versa. Type conversions can take advantage of certain features of type hierarchies or data representations. Two important aspects of a type conversion are whether it happens ''implicitly'' (automatically) or ''explicitly'', and whether the underlying data representation is converted from one representation into another, or a given representation is merely ''reinterpreted'' as the representation of another data type. In general, both primitive and compound data types can be converted. Each programming language has its own rules on how types can be converted. Languages with strong typing typically do little implicit conversion and discourage the reinterpretation of representations, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Division By Zero
In mathematics, division by zero, division (mathematics), division where the divisor (denominator) is 0, zero, is a unique and problematic special case. Using fraction notation, the general example can be written as \tfrac a0, where a is the dividend (numerator). The usual definition of the quotient in elementary arithmetic is the number which yields the dividend when multiplication, multiplied by the divisor. That is, c = \tfrac ab is equivalent to c \cdot b = a. By this definition, the quotient q = \tfrac is nonsensical, as the product q \cdot 0 is always 0 rather than some other number a. Following the ordinary rules of elementary algebra while allowing division by zero can create a mathematical fallacy, a subtle mistake leading to absurd results. To prevent this, the arithmetic of real numbers and more general numerical structures called field (mathematics), fields leaves division by zero undefined (mathematics), undefined, and situations where division by zero might occur m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Type Punning
In computer science, a type punning is any programming technique that subverts or circumvents the type system of a programming language in order to achieve an effect that would be difficult or impossible to achieve within the bounds of the formal language. In C and C++, constructs such as pointer type conversion and union — C++ adds reference type conversion and reinterpret_cast to this list — are provided in order to permit many kinds of type punning, although some kinds are not actually supported by the standard language. In the Pascal programming language, the use of records with variants may be used to treat a particular data type in more than one manner, or in a manner not normally permitted. Sockets example One classic example of type punning is found in the Berkeley sockets interface. The function to bind an opened but uninitialized socket to an IP address is declared as follows: int bind(int sockfd, struct sockaddr *my_addr, socklen_t addrlen); The bind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Java Programming Language
Java is a high-level, general-purpose, memory-safe, object-oriented programming language. It is intended to let programmers ''write once, run anywhere'' ( WORA), meaning that compiled Java code can run on all platforms that support Java without the need to recompile. Java applications are typically compiled to bytecode that can run on any Java virtual machine (JVM) regardless of the underlying computer architecture. The syntax of Java is similar to C and C++, but has fewer low-level facilities than either of them. The Java runtime provides dynamic capabilities (such as reflection and runtime code modification) that are typically not available in traditional compiled languages. Java gained popularity shortly after its release, and has been a popular programming language since then. Java was the third most popular programming language in according to GitHub. Although still widely popular, there has been a gradual decline in use of Java in recent years with other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
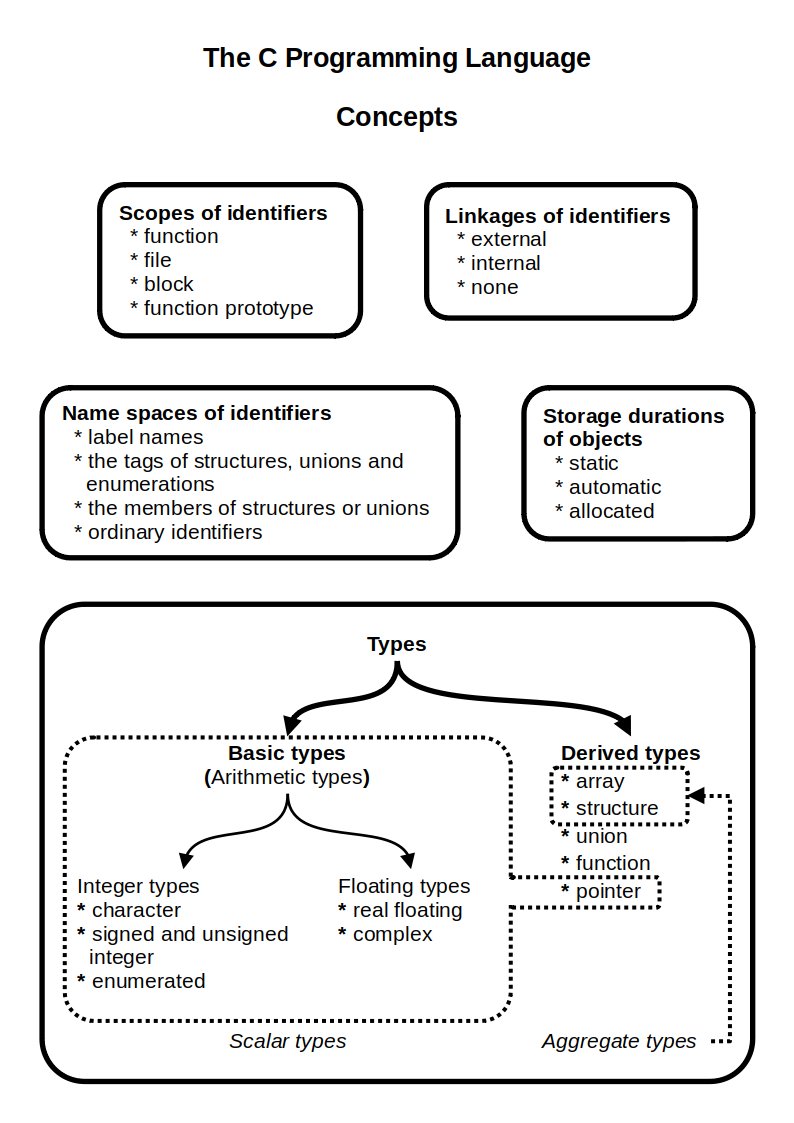
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exception Handling
In computing and computer programming, exception handling is the process of responding to the occurrence of ''exceptions'' – anomalous or exceptional conditions requiring special processing – during the execution of a program. In general, an exception breaks the normal flow of execution and executes a pre-registered ''exception handler''; the details of how this is done depend on whether it is a hardware or software exception and how the software exception is implemented. Exceptions are defined by different layers of a computer system, and the typical layers are CPU-defined interrupts, operating system (OS)-defined signals, programming language-defined exceptions. Each layer requires different ways of exception handling although they may be interrelated, e.g. a CPU interrupt could be turned into an OS signal. Some exceptions, especially hardware ones, may be handled so gracefully that execution can resume where it was interrupted. Definition The definition of an excep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Indeterminate Form
Indeterminate form is a mathematical expression that can obtain any value depending on circumstances. In calculus, it is usually possible to compute the limit of the sum, difference, product, quotient or power of two functions by taking the corresponding combination of the separate limits of each respective function. For example, \begin \lim_ \bigl(f(x) + g(x)\bigr) &= \lim_ f(x) + \lim_ g(x), \\ mu\lim_ \bigl(f(x)g(x)\bigr) &= \lim_ f(x) \cdot \lim_ g(x), \end and likewise for other arithmetic operations; this is sometimes called the algebraic limit theorem. However, certain combinations of particular limiting values cannot be computed in this way, and knowing the limit of each function separately does not suffice to determine the limit of the combination. In these particular situations, the limit is said to take an indeterminate form, described by one of the informal expressions \frac 00,~ \frac,~ 0\times\infty,~ \infty - \infty,~ 0^0,~ 1^\infty, \text \infty^0, among a wide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
IBM Corporation
International Business Machines Corporation (using the trademark IBM), nicknamed Big Blue, is an American multinational technology company headquartered in Armonk, New York, and present in over 175 countries. It is a publicly traded company and one of the 30 companies in the Dow Jones Industrial Average. IBM is the largest industrial research organization in the world, with 19 research facilities across a dozen countries; for 29 consecutive years, from 1993 to 2021, it held the record for most annual U.S. patents generated by a business. IBM was founded in 1911 as the Computing-Tabulating-Recording Company (CTR), a holding company of manufacturers of record-keeping and measuring systems. It was renamed "International Business Machines" in 1924 and soon became the leading manufacturer of punch-card tabulating systems. During the 1960s and 1970s, the IBM mainframe, exemplified by the System/360 and its successors, was the world's dominant computing platform, with the compa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arithmetic Underflow
The term arithmetic underflow (also floating-point underflow, or just underflow) is a condition in a computer program where the result of a calculation is a number of more precise absolute value than the computer can actually represent in memory on its central processing unit (CPU). Arithmetic underflow can occur when the true result of a floating-point operation is smaller in magnitude (that is, closer to zero) than the smallest value representable as a normal floating-point number in the target datatype. Underflow can in part be regarded as negative overflow of the exponent of the floating-point value. For example, if the exponent part can represent values from −128 to 127, then a result with a value less than −128 may cause underflow. Underflow gap The interval between −''fminN'' and ''fminN'', where ''fminN'' is the smallest positive normal floating-point value, is called the underflow gap. This is because the size of this interval is many orders of magnitude ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |