|
Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime. As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. He is also considered to be one of the founders of the field of topology. Poincaré made clear the importance of paying attention to the invariance of laws of physics under different transformations, and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré disc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nancy, France
Nancy ; Lorraine Franconian: ''Nanzisch'' is the prefecture of the northeastern French department of Meurthe-et-Moselle. It was the capital of the Duchy of Lorraine, which was annexed by France under King Louis XV in 1766 and replaced by a province, with Nancy maintained as capital. Following its rise to prominence in the Age of Enlightenment, it was nicknamed the "capital of Eastern France" in the late 19th century. The metropolitan area of Nancy had a population of 511,257 inhabitants at the 2018 census, making it the 16th-largest functional urban area in France and Lorraine's largest. The population of the city of Nancy proper is 104,885. The motto of the city is , —a reference to the thistle, which is a symbol of Lorraine. Place Stanislas, a large square built between 1752 and 1756 by architect Emmanuel Héré under the direction of Stanislaus I of Poland to link the medieval old town of Nancy and the new city built under Charles III, Duke of Lorraine in the 17th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Conjecture
In the mathematical field of geometric topology, the Poincaré conjecture (, , ) is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space. Originally conjectured by Henri Poincaré in 1904, the Grigori Perelman's theorem concerns spaces that locally look like ordinary three-dimensional space but which are finite in extent. Poincaré hypothesized that if such a space has the additional property that each loop in the space can be continuously tightened to a point, then it is necessarily a three-dimensional sphere. Attempts to resolve the conjecture drove much progress in the field of geometric topology during the 20th century. The Perelman's proof built upon Richard S. Hamilton's ideas of using the Ricci flow to solve the problem. By developing a number of breakthrough new techniques and results in the theory of Ricci flow, Grigori Perelman was able to prove the Conjecture, and more than just t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
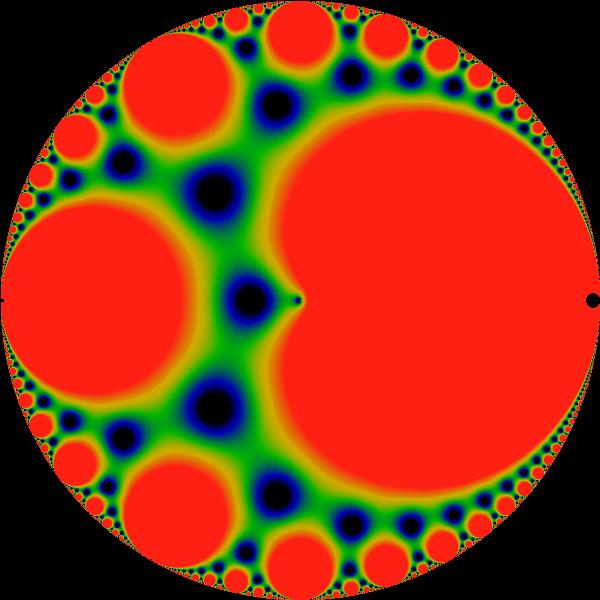
Poincaré Metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces. There are three equivalent representations commonly used in two-dimensional hyperbolic geometry. One is the Poincaré half-plane model, defining a model of hyperbolic space on the upper half-plane. The Poincaré disk model defines a model for hyperbolic space on the unit disk. The disk and the upper half plane are related by a conformal map, and isometries are given by Möbius transformations. A third representation is on the punctured disk, where relations for ''q''-analogues are sometimes expressed. These various forms are reviewed below. Overview of metrics on Riemann surfaces A metric on the complex plane may be generally expressed in the form :ds^2=\lambda^2(z,\overline)\, dz\,d\overline where λ is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Series (modular Form)
In number theory, a Poincaré series is a mathematical series generalizing the classical theta series that is associated to any discrete group of symmetries of a complex domain, possibly of several complex variables. In particular, they generalize classical Eisenstein series. They are named after Henri Poincaré. If Γ is a finite group acting on a domain ''D'' and ''H''(''z'') is any meromorphic function on ''D'', then one obtains an automorphic function by averaging over Γ: :\sum_ H(\gamma(z)). However, if Γ is a discrete group, then additional factors must be introduced in order to assure convergence of such a series. To this end, a Poincaré series is a series of the form :\theta_k(z) = \sum_ (J_\gamma(z))^k H(\gamma(z)) where ''J''γ is the Jacobian determinant of the group element γ,Or a more general factor of automorphy as discussed in . and the asterisk denotes that the summation takes place only over coset representatives yielding distinct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert–Poincaré Series
In mathematics, and in particular in the field of algebra, a Hilbert–Poincaré series (also known under the name Hilbert series), named after David Hilbert and Henri Poincaré, is an adaptation of the notion of dimension to the context of graded algebraic structures (where the dimension of the entire structure is often infinite). It is a formal power series in one indeterminate, say t, where the coefficient of t^n gives the dimension (or rank) of the sub-structure of elements homogeneous of degree n. It is closely related to the Hilbert polynomial in cases when the latter exists; however, the Hilbert–Poincaré series describes the rank in every degree, while the Hilbert polynomial describes it only in all but finitely many degrees, and therefore provides less information. In particular the Hilbert–Poincaré series cannot be deduced from the Hilbert polynomial even if the latter exists. In good cases, the Hilbert–Poincaré series can be expressed as a rational function of i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great importance in the modern, direct methods of the calculus of variations. A very closely related result is Friedrichs' inequality. Statement of the inequality The classical Poincaré inequality Let ''p'', so that 1 ≤ ''p'' < ∞ and Ω a subset bounded at least in one direction. Then there exists a constant ''C'', depending only on Ω and ''p'', so that, for every function ''u'' of the Sobolev space ''W''01,''p''(Ω) of zero-trace (a.k.a. zero on the boundary) functions, : Poincaré–Wirtin ...
|
Poincaré–Birkhoff–Witt Theorem
In mathematics, more specifically in the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem (or PBW theorem) is a result giving an explicit description of the universal enveloping algebra of a Lie algebra. It is named after Henri Poincaré, Garrett Birkhoff, and Ernst Witt. The terms ''PBW type theorem'' and ''PBW theorem'' may also refer to various analogues of the original theorem, comparing a filtered algebra to its associated graded algebra, in particular in the area of quantum groups. Statement of the theorem Recall that any vector space ''V'' over a field has a basis; this is a set ''S'' such that any element of ''V'' is a unique (finite) linear combination of elements of ''S''. In the formulation of Poincaré–Birkhoff–Witt theorem we consider bases of which the elements are totally ordered by some relation which we denote ≤. If ''L'' is a Lie algebra over a field K, let ''h'' denote the canonical K-linear map from ''L'' into the universal envelo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Duality
In mathematics, the Poincaré duality theorem, named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds. It states that if ''M'' is an ''n''-dimensional oriented closed manifold (compact and without boundary), then the ''k''th cohomology group of ''M'' is isomorphic to the (n-k)th homology group of ''M'', for all integers ''k'' :H^k(M) \cong H_(M). Poincaré duality holds for any coefficient ring, so long as one has taken an orientation with respect to that coefficient ring; in particular, since every manifold has a unique orientation mod 2, Poincaré duality holds mod 2 without any assumption of orientation. History A form of Poincaré duality was first stated, without proof, by Henri Poincaré in 1893. It was stated in terms of Betti numbers: The ''k''th and (n-k)th Betti numbers of a closed (i.e., compact and without boundary) orientable ''n''-manifold are equal. The ''cohomology'' concept was at that time about 4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré–Hopf Theorem
In mathematics, the Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is used in differential topology. It is named after Henri Poincaré and Heinz Hopf. The Poincaré–Hopf theorem is often illustrated by the special case of the hairy ball theorem, which simply states that there is no smooth vector field on an even-dimensional n-sphere having no sources or sinks. Formal statement Let M be a differentiable manifold, of dimension n, and v a vector field on M. Suppose that x is an isolated zero of v, and fix some local coordinates near x. Pick a closed ball D centered at x, so that x is the only zero of v in D. Then the index of v at x, \operatorname_x(v), can be defined as the degree of the map u : \partial D \to \mathbb S^ from the boundary of D to the (n-1)-sphere given by u(z)=v(z)/\, v(z)\, . Theorem. Let M be a compact differentiable manifold. Let v be a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Gauge
In the physics of gauge theories, gauge fixing (also called choosing a gauge) denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a gauge transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom. Although the unphysical axes in the space of detailed configurations are a fundamental property of the physical model, there is no special set of directions "perpendicular" to them. Hence there is an enormous amount of freedom involved in taking a "cross section" representing each physical configuration by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Group
The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our understanding of the most basic fundamentals of physics. Overview A Minkowski spacetime isometry has the property that the interval between events is left invariant. For example, if everything were postponed by two hours, including the two events and the path you took to go from one to the other, then the time interval between the events recorded by a stop-watch you carried with you would be the same. Or if everything were shifted five kilometres to the west, or turned 60 degrees to the right, you would also see no change in the interval. It turns out that the proper length of an object is also unaffected by such a shift. A time or space reversal (a reflection) is also an isometry of this group. In Minkowski space (i.e. ignoring the effec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kelvin's Circulation Theorem
In fluid mechanics, Kelvin's circulation theorem (named after William Thomson, 1st Baron Kelvin William Thomson, 1st Baron Kelvin, (26 June 182417 December 1907) was a British mathematician, Mathematical physics, mathematical physicist and engineer born in Belfast. Professor of Natural Philosophy (Glasgow), Professor of Natural Philoso ... who published it in 1869) states:In a barotropic, ideal fluid with Conservative force, conservative body forces, the Circulation (fluid dynamics), circulation around a closed curve (which encloses the same fluid elements) moving with the fluid remains constant with time. Stated mathematically: :\frac = 0 where \Gamma is the Circulation (fluid dynamics), circulation around a material contour C(t). Stated more simply, this theorem says that if one observes a closed contour at one instant, and follows the contour over time (by following the motion of all of its fluid elements), the circulation over the two locations of this contour are equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |