ultraparallel theorem

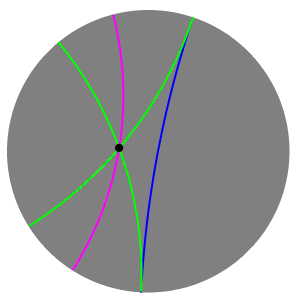In hyperbolic geometry, two lines may intersect, be ultraparallel, or be limiting parallel.

The ultraparallel theorem states that every pair of (distinct) ultraparallel lines has a unique common perpendicular (a hyperbolic line which is perpendicular to both lines).

Hilbert's construction

Let r and s be two ultraparallel lines.

From any two distinct points A and C on s draw AB and CB' perpendicular to r with B and B' on r.

If it happens that AB = CB', then the desired common perpendicular joins the midpoints of AC and BB' (by the symmetry of the Saccheri quadrilateral ACB'B).

If not, we may suppose AB < CB' without loss of generality. Let E be a point on the line s on the opposite side of A from C. Take A' on CB' so that A'B' = AB. Through A' draw a line s' (A'E') on the side closer to E, so that the angle B'A'E' is the same as angle BAE. Then s' meets s in an ordinary point D'. Construct a point D on ray AE so that AD = A'D'.

Then D' ≠ D. They are the same distance from r and both lie on s. So the perpendicular bisector of D'D (a segment of s) is also perpendicular to r.

(If r and s were asymptotically parallel rather than ultraparallel, this construction would fail because s' would not meet s. Rather s' would be asymptotically parallel to both s and r.)

Proof in the Poincaré half-plane model

Let
:$a < b < c < d$

be four distinct points on the abscissa of the Cartesian plane. Let $p$ and $q$ be semicircles above the abscissa with diameters $ab$ and $cd$ respectively. Then in the Poincaré half-plane model HP, $p$ and $q$ represent ultraparallel lines.

Compose the following two hyperbolic motions:

:$x \to x-a$
:$\mbox$

Then $a \to \infty, \quad b \to (b-a)^,\quad c \to (c-a)^,\quad d \to (d-a)^.$

Now continue with these two hyperbolic motions:
:$x \to x-(b-a)^$
:x \to \left (c-a)^ - (b-a)^ \right x

Then $a$ stays at $\infty$, $b \to 0$, $c \to 1$, $d \to z$ (say). The unique semicircle, with center at the origin, perpendicular to the one on $1z$ must have a radius tangent to the radius of the other. The right triangle formed by the abscissa and the perpendicular radii has hypotenuse of length $\begin \frac \end (z+1)$. Since $\begin \frac \end (z-1)$ is the radius of the semicircle on $1z$, the common perpendicular sought has radius-square

:\frac \left (z+1)^2 - (z-1)^2 \right = z.

The four hyperbolic motions that produced $z$ above can each be inverted and applied in reverse order to the semicircle centered at the origin and of radius $\sqrt$ to yield the unique hyperbolic line perpendicular to both ultraparallels $p$ and $q$.

Proof in the Beltrami-Klein model

In the Beltrami-Klein model of the hyperbolic geometry:
* two ultraparallel lines correspond to two non-intersecting chords.
* The poles of these two lines are the respective intersections of the tangent lines to the boundary circle at the endpoints of the chords.
* Lines ''perpendicular'' to line ''l'' are modeled by chords whose extension passes through the pole of ''l''.
* Hence we draw the unique line between the poles of the two given lines, and intersect it with the boundary circle ; the chord of intersection will be the desired common perpendicular of the ultraparallel lines.

If one of the chords happens to be a diameter, we do not have a pole, but in this case any chord perpendicular to the diameter it is also perpendicular in the Beltrami-Klein model, and so we draw a line through the pole of the other line intersecting the diameter at right angles to get the common perpendicular.

The proof is completed by showing this construction is always possible:

* If both chords are diameters, they intersect.(at the center of the boundary circle)
* If only one of the chords is a diameter, the other chord projects orthogonally down to a section of the first chord contained in its interior, and a line from the pole orthogonal to the diameter intersects both the diameter and the chord.
* If both lines are not diameters, then we may extend the tangents drawn from each pole to produce a quadrilateral with the unit circle inscribed within it. The poles are opposite vertices of this quadrilateral, and the chords are lines drawn between adjacent sides of the vertex, across opposite corners. Since the quadrilateral is convex, the line between the poles intersects both of the chords drawn across the corners, and the segment of the line between the chords defines the required chord perpendicular to the two other chords.

Alternatively, we can construct the common perpendicular of the ultraparallel lines as follows: the ultraparallel lines in Beltrami-Klein model are two non-intersecting chords. But they actually intersect outside the circle. The polar of the intersecting point is the desired common perpendicular.W. Thurston, ''Three-Dimensional Geometry and Topology'', page 72

References

{{Reflist
* Karol Borsuk & Wanda Szmielew (1960) ''Foundations of Geometry'', page 291.

Articles containing proofs
Hyperbolic geometry
Theorems in geometry