Trigonometric Function on:
[Wikipedia]
[Google]
[Amazon]
 In
In

 If the acute angle is given, then any right triangles that have an angle of are similar to each other. This means that the ratio of any two side lengths depends only on . Thus these six ratios define six functions of , which are the trigonometric functions. In the following definitions, the hypotenuse is the length of the side opposite the right angle, ''opposite'' represents the side opposite the given angle , and ''adjacent'' represents the side between the angle and the right angle.
In a right-angled triangle, the sum of the two acute angles is a right angle, that is, or . Therefore and represent the same ratio, and thus are equal. This identity and analogous relationships between the other trigonometric functions are summarized in the following table.
If the acute angle is given, then any right triangles that have an angle of are similar to each other. This means that the ratio of any two side lengths depends only on . Thus these six ratios define six functions of , which are the trigonometric functions. In the following definitions, the hypotenuse is the length of the side opposite the right angle, ''opposite'' represents the side opposite the given angle , and ''adjacent'' represents the side between the angle and the right angle.
In a right-angled triangle, the sum of the two acute angles is a right angle, that is, or . Therefore and represent the same ratio, and thus are equal. This identity and analogous relationships between the other trigonometric functions are summarized in the following table.

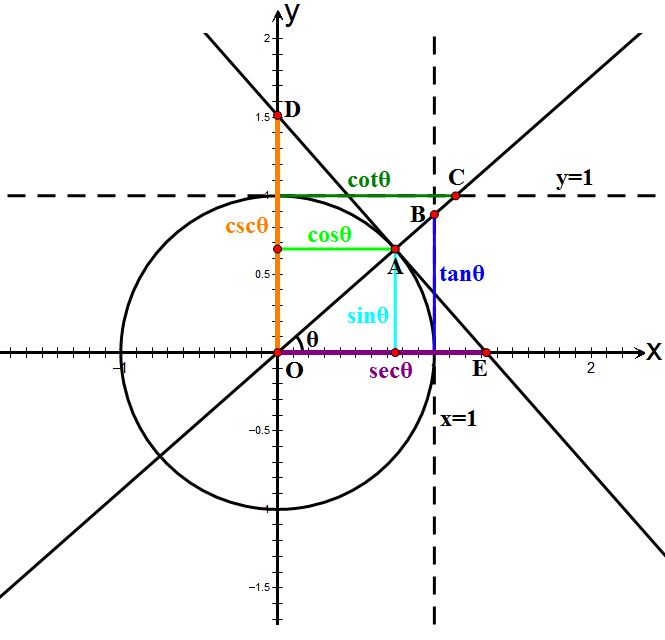 The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the
The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the  Since a rotation of an angle of does not change the position or size of a shape, the points , , , , and are the same for two angles whose difference is an integer multiple of . Thus trigonometric functions are
Since a rotation of an angle of does not change the position or size of a shape, the points , , , , and are the same for two angles whose difference is an integer multiple of . Thus trigonometric functions are
 The
The

 The modern trend in mathematics is to build
The modern trend in mathematics is to build



 The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motion, which models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motion.
Trigonometric functions also prove to be useful in the study of general
The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motion, which models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motion.
Trigonometric functions also prove to be useful in the study of general
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, such as navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation ...
, solid mechanics, celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, ...
, geodesy, and many others. They are among the simplest periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to des ...
s, and as such are also widely used for studying periodic phenomena through Fourier analysis.
The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
s are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions.
The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ar ...
s. To extend the sine and cosine functions to functions whose domain
Domain may refer to:
Mathematics
*Domain of a function, the set of input values for which the (total) function is defined
** Domain of definition of a partial function
** Natural domain of a partial function
**Domain of holomorphy of a function
* ...
is the whole real line, geometrical definitions using the standard unit circle (i.e., a circle with radius
In classical geometry, a radius (plural, : radii) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', ...
1 unit) are often used; then the domain of the other functions is the real line with some isolated points removed. Modern definitions express trigonometric functions as infinite series or as solutions of differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, ...
s. This allows extending the domain of sine and cosine functions to the whole complex plane, and the domain of the other trigonometric functions to the complex plane with some isolated points removed.
Notation
Conventionally, an abbreviation of each trigonometric function's name is used as its symbol in formulas. Today, the most common versions of these abbreviations are "sin" for sine, "cos" for cosine, "tan" or "tg" for tangent, "sec" for secant, "csc" or "cosec" for cosecant, and "cot" or "ctg" for cotangent. Historically, these abbreviations were first used in prose sentences to indicate particular line segments or their lengths related to an arc of an arbitrary circle, and later to indicate ratios of lengths, but as the function concept developed in the 17th–18th century, they began to be considered as functions of real-number-valued angle measures, and written with functional notation, for example . Parentheses are still often omitted to reduce clutter, but are sometimes necessary; for example the expression would typically be interpreted to mean so parentheses are required to express A positive integer appearing as a superscript after the symbol of the function denotesexponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to ...
, not function composition. For example and denote not This differs from the (historically later) general functional notation in which
However, the exponent is commonly used to denote the inverse function, not the reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
. For example and denote the inverse trigonometric function alternatively written The equation implies not In this case, the superscript ''could'' be considered as denoting a composed or iterated function, but negative superscripts other than are not in common use.
Right-angled triangle definitions
Radians versus degrees
In geometric applications, the argument of a trigonometric function is generally the measure of anangle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ...
. For this purpose, any angular unit is convenient, and angles are most commonly measured in conventional units of degrees in which a right angle is 90° and a complete turn is 360° (particularly in elementary mathematics).
However, in calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
and mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limits, and related theories, such as differentiation, integration, measure, infinite sequences, series, and analytic functions.
These theories are usually studied ...
, the trigonometric functions are generally regarded more abstractly as functions of real or complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s, rather than angles. In fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
via power series or as solutions to differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, ...
s given particular initial values (''see below''), without reference to any geometric notions. The other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator. It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions ''if'' ''the argument is regarded as an angle given in radians''. Moreover, these definitions result in simple expressions for the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
s and indefinite integrals
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically ...
for the trigonometric functions. Thus, in settings beyond elementary geometry, radians are regarded as the mathematically natural unit for describing angle measures.
When radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that ...
s (rad) are employed, the angle is given as the length of the arc of the unit circle subtended by it: the angle that subtends an arc of length 1 on the unit circle is 1 rad (≈ 57.3°), and a complete turn (360°) is an angle of 2 (≈ 6.28) rad. For real number ''x'', the notations sin ''x'', cos ''x'', etc. refer to the value of the trigonometric functions evaluated at an angle of ''x'' rad. If units of degrees are intended, the degree sign must be explicitly shown (e.g., sin ''x°'', cos ''x°'', etc.). Using this standard notation, the argument ''x'' for the trigonometric functions satisfies the relationship ''x'' = (180''x''/)°, so that, for example, sin = sin 180° when we take ''x'' = . In this way, the degree symbol can be regarded as a mathematical constant such that 1° = /180 ≈ 0.0175.
Unit-circle definitions
 The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the
The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
of radius one centered at the origin of this coordinate system. While right-angled triangle definitions allow for the definition of the trigonometric functions for angles between and radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that ...
s the unit circle definitions allow the domain of trigonometric functions to be extended to all positive and negative real numbers.
Let be the ray
Ray may refer to:
Fish
* Ray (fish), any cartilaginous fish of the superorder Batoidea
* Ray (fish fin anatomy), a bony or horny spine on a fin
Science and mathematics
* Ray (geometry), half of a line proceeding from an initial point
* Ray (gr ...
obtained by rotating by an angle the positive half of the -axis (counterclockwise
Two-dimensional rotation can occur in two possible directions. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back up to the top. The opposite ...
rotation for and clockwise rotation for ). This ray intersects the unit circle at the point The ray extended to a line if necessary, intersects the line of equation at point and the line of equation at point The tangent line to the unit circle at the point , is perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. It c ...
to and intersects the - and -axes at points and The coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
of these points give the values of all trigonometric functions for any arbitrary real value of in the following manner.
The trigonometric functions and are defined, respectively, as the ''x''- and ''y''-coordinate values of point . That is,
: and
In the range , this definition coincides with the right-angled triangle definition, by taking the right-angled triangle to have the unit radius as hypotenuse. And since the equation holds for all points on the unit circle, this definition of cosine and sine also satisfies the Pythagorean identity.
:
The other trigonometric functions can be found along the unit circle as
: and
: and
By applying the Pythagorean identity and geometric proof methods, these definitions can readily be shown to coincide with the definitions of tangent, cotangent, secant and cosecant in terms of sine and cosine, that is
:
periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to des ...
s with period . That is, the equalities
: and
hold for any angle and any integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
. The same is true for the four other trigonometric functions. By observing the sign and the monotonicity of the functions sine, cosine, cosecant, and secant in the four quadrants, one can show that is the smallest value for which they are periodic (i.e., is the fundamental period of these functions). However, after a rotation by an angle , the points and already return to their original position, so that the tangent function and the cotangent function have a fundamental period of . That is, the equalities
: and
hold for any angle and any integer .
Algebraic values
algebraic expression In mathematics, an algebraic expression is an expression built up from integer constants, variables, and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number). ...
s for the most important angles are as follows:
: ( zero angle)
:
:
:
: ( right angle)
Writing the numerators as square roots of consecutive non-negative integers, with a denominator of 2, provides an easy way to remember the values.
Such simple expressions generally do not exist for other angles which are rational multiples of a right angle.
*For an angle which, measured in degrees, is a multiple of three, the exact trigonometric values of the sine and the cosine may be expressed in terms of square roots. These values of the sine and the cosine may thus be constructed by ruler and compass.
*For an angle of an integer number of degrees, the sine and the cosine may be expressed in terms of square roots and the cube root of a non-real complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
. Galois theory allows a proof that, if the angle is not a multiple of 3°, non-real cube roots are unavoidable.
*For an angle which, expressed in degrees, is a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
, the sine and the cosine are algebraic numbers, which may be expressed in terms of th roots. This results from the fact that the Galois groups of the cyclotomic polynomials are cyclic
Cycle, cycles, or cyclic may refer to:
Anthropology and social sciences
* Cyclic history, a theory of history
* Cyclical theory, a theory of American political history associated with Arthur Schlesinger, Sr.
* Social cycle, various cycles in so ...
.
*For an angle which, expressed in degrees, is not a rational number, then either the angle or both the sine and the cosine are transcendental numbers. This is a corollary of Baker's theorem, proved in 1966.
Simple algebraic values
The following table lists the sines, cosines, and tangents of multiples of 15 degrees from 0 to 90 degrees.In calculus
Graphs of sine, cosine and tangentgeometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
from calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
rather than the converse. Therefore, except at a very elementary level, trigonometric functions are defined using the methods of calculus.
Trigonometric functions are differentiable and analytic
Generally speaking, analytic (from el, ἀναλυτικός, ''analytikos'') refers to the "having the ability to analyze" or "division into elements or principles".
Analytic or analytical can also have the following meanings:
Chemistry
* ...
at every point where they are defined; that is, everywhere for the sine and the cosine, and, for the tangent, everywhere except at for every integer .
The trigonometric function are periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to des ...
s, and their primitive period is for the sine and the cosine, and for the tangent, which is increasing in each open interval . At each end point of these intervals, the tangent function has a vertical asymptote.
In calculus, there are two equivalent definitions of trigonometric functions, either using power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a con ...
or differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, ...
s. These definitions are equivalent, as starting from one of them, it is easy to retrieve the other as a property. However the definition through differential equations is somehow more natural, since, for example, the choice of the coefficients of the power series may appear as quite arbitrary, and the Pythagorean identity is much easier to deduce from the differential equations.
Definition by differential equations
Sine and cosine can be defined as the unique solution to theinitial value problem
In multivariable calculus, an initial value problem (IVP) is an ordinary differential equation together with an initial condition which specifies the value of the unknown function at a given point in the domain. Modeling a system in physics or o ...
:
:
Differentiating again, and , so both sine and cosine are solutions of the ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast ...
:
Applying the quotient rule to the tangent , we derive
:
Power series expansion
Applying the differential equations topower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a con ...
with indeterminate coefficients, one may deduce recurrence relations for the coefficients of the Taylor series of the sine and cosine functions. These recurrence relations are easy to solve, and give the series expansions
:
The radius of convergence of these series is infinite. Therefore, the sine and the cosine can be extended to entire functions (also called "sine" and "cosine"), which are (by definition) complex-valued functions that are defined and holomorphic on the whole complex plane.
Being defined as fractions of entire functions, the other trigonometric functions may be extended to meromorphic functions, that is functions that are holomorphic in the whole complex plane, except some isolated points called poles
Poles,, ; singular masculine: ''Polak'', singular feminine: ''Polka'' or Polish people, are a West Slavic nation and ethnic group, who share a common history, culture, the Polish language and are identified with the country of Poland in ...
. Here, the poles are the numbers of the form for the tangent and the secant, or for the cotangent and the cosecant, where is an arbitrary integer.
Recurrences relations may also be computed for the coefficients of the Taylor series of the other trigonometric functions. These series have a finite radius of convergence. Their coefficients have a combinatorial interpretation: they enumerate alternating permutations of finite sets.
More precisely, defining
: , the th up/down number,
: , the th Bernoulli number, and
: , is the th Euler number,
one has the following series expansions:
:
:
:
:
Continued fraction expansion
The following expansions are valid in the whole complex plane: : : : The last one was used in the historically first proof that π is irrational.Partial fraction expansion
There is a series representation aspartial fraction expansion
In algebra, the partial fraction decomposition or partial fraction expansion of a rational fraction (that is, a fraction such that the numerator and the denominator are both polynomials) is an operation that consists of expressing the fraction as ...
where just translated reciprocal functions are summed up, such that the poles of the cotangent function and the reciprocal functions match:
:
This identity can be proved with the Herglotz trick.
Combining the th with the th term lead to absolutely convergent series:
:
Similarly, one can find a partial fraction expansion for the secant, cosecant and tangent functions:
:
:
:
:
Infinite product expansion
The following infinite product for the sine is of great importance in complex analysis: : For the proof of this expansion, see Sine. From this, it can be deduced that :Relationship to exponential function (Euler's formula)
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that ...
relates sine and cosine to the exponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
:
:
This formula is commonly considered for real values of , but it remains true for all complex values.
''Proof'': Let and One has for . The quotient rule implies thus that . Therefore, is a constant function, which equals , as This proves the formula.
One has
:
Solving this linear system
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator.
Linear systems typically exhibit features and properties that are much simpler than the nonlinear case.
As a mathematical abstraction ...
in sine and cosine, one can express them in terms of the exponential function:
:
When is real, this may be rewritten as
:
Most trigonometric identities can be proved by expressing trigonometric functions in terms of the complex exponential function by using above formulas, and then using the identity for simplifying the result.
Definitions using functional equations
One can also define the trigonometric functions using various functional equations. For example, the sine and the cosine form the unique pair ofcontinuous function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in val ...
s that satisfy the difference formula
:
and the added condition
:
In the complex plane
The sine and cosine of acomplex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
can be expressed in terms of real sines, cosines, and hyperbolic function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the u ...
s as follows:
:
By taking advantage of domain coloring, it is possible to graph the trigonometric functions as complex-valued functions. Various features unique to the complex functions can be seen from the graph; for example, the sine and cosine functions can be seen to be unbounded as the imaginary part of becomes larger (since the color white represents infinity), and the fact that the functions contain simple zeros or poles is apparent from the fact that the hue cycles around each zero or pole exactly once. Comparing these graphs with those of the corresponding Hyperbolic functions highlights the relationships between the two.
Basic identities
Many identities interrelate the trigonometric functions. This section contains the most basic ones; for more identities, see List of trigonometric identities. These identities may be proved geometrically from the unit-circle definitions or the right-angled-triangle definitions (although, for the latter definitions, care must be taken for angles that are not in the interval , seeProofs of trigonometric identities
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of ...
). For non-geometrical proofs using only tools of calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
, one may use directly the differential equations, in a way that is similar to that of the above proof of Euler's identity. One can also use Euler's identity for expressing all trigonometric functions in terms of complex exponentials and using properties of the exponential function.
Parity
The cosine and the secant areeven function
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power se ...
s; the other trigonometric functions are odd function
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power se ...
s. That is:
:
Periods
All trigonometric functions areperiodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to des ...
s of period . This is the smallest period, except for the tangent and the cotangent, which have as smallest period. This means that, for every integer , one has
:
Pythagorean identity
The Pythagorean identity, is the expression of the Pythagorean theorem in terms of trigonometric functions. It is :. Dividing through by either or gives : and :.Sum and difference formulas
The sum and difference formulas allow expanding the sine, the cosine, and the tangent of a sum or a difference of two angles in terms of sines and cosines and tangents of the angles themselves. These can be derived geometrically, using arguments that date toPtolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importanc ...
. One can also produce them algebraically using Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that ...
.
; Sum
:
; Difference
:
When the two angles are equal, the sum formulas reduce to simpler equations known as the double-angle formulae.
:
These identities can be used to derive the product-to-sum identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
.
By setting all trigonometric functions of can be expressed as rational fractions of :
:
Together with
:
this is the tangent half-angle substitution, which reduces the computation of integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
s and antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolica ...
s of trigonometric functions to that of rational fractions.
Derivatives and antiderivatives
Thederivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
s of trigonometric functions result from those of sine and cosine by applying quotient rule. The values given for the antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolica ...
s in the following table can be verified by differentiating them. The number is a constant of integration
In calculus, the constant of integration, often denoted by C (or c), is a constant term added to an antiderivative of a function f(x) to indicate that the indefinite integral of f(x) (i.e., the set of all antiderivatives of f(x)), on a connecte ...
.
Alternatively, the derivatives of the 'co-functions' can be obtained using trigonometric identities and the chain rule:
:
Inverse functions
The trigonometric functions are periodic, and hence not injective, so strictly speaking, they do not have an inverse function. However, on each interval on which a trigonometric function ismonotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
, one can define an inverse function, and this defines inverse trigonometric functions as multivalued functions. To define a true inverse function, one must restrict the domain to an interval where the function is monotonic, and is thus bijective from this interval to its image by the function. The common choice for this interval, called the set of principal values, is given in the following table. As usual, the inverse trigonometric functions are denoted with the prefix "arc" before the name or its abbreviation of the function.
The notations , , etc. are often used for and , etc. When this notation is used, inverse functions could be confused with multiplicative inverses. The notation with the "arc" prefix avoids such a confusion, though "arcsec" for arcsecant can be confused with " arcsecond".
Just like the sine and cosine, the inverse trigonometric functions can also be expressed in terms of infinite series. They can also be expressed in terms of complex logarithms.
Applications
Angles and sides of a triangle
In this section , , denote the three (interior) angles of a triangle, and , , denote the lengths of the respective opposite edges. They are related by various formulas, which are named by the trigonometric functions they involve.Law of sines
The law of sines states that for an arbitrary triangle with sides , , and and angles opposite those sides , and : where is the area of the triangle, or, equivalently, where is the triangle'scircumradius
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every pol ...
.
It can be proved by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in '' triangulation'', a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Law of cosines
The law of cosines (also known as the cosine formula or cosine rule) is an extension of the Pythagorean theorem: or equivalently, In this formula the angle at is opposite to the side . This theorem can be proved by dividing the triangle into two right ones and using the Pythagorean theorem. The law of cosines can be used to determine a side of a triangle if two sides and the angle between them are known. It can also be used to find the cosines of an angle (and consequently the angles themselves) if the lengths of all the sides are known.Law of tangents
The law of tangents says that: :.Law of cotangents
If ''s'' is the triangle's semiperimeter, (''a'' + ''b'' + ''c'')/2, and ''r'' is the radius of the triangle's incircle, then ''rs'' is the triangle's area. Therefore Heron's formula implies that: :. The law of cotangents says that: : It follows that :Periodic functions

 The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motion, which models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motion.
Trigonometric functions also prove to be useful in the study of general
The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motion, which models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motion.
Trigonometric functions also prove to be useful in the study of general periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to des ...
s. The characteristic wave patterns of periodic functions are useful for modeling recurring phenomena such as sound or light waves.
Under rather general conditions, a periodic function can be expressed as a sum of sine waves or cosine waves in a Fourier series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or '' ...
. Denoting the sine or cosine basis functions by , the expansion of the periodic function takes the form:
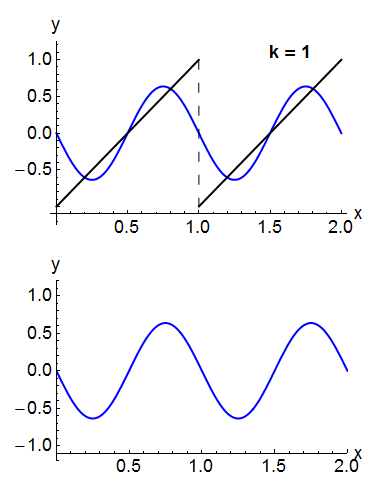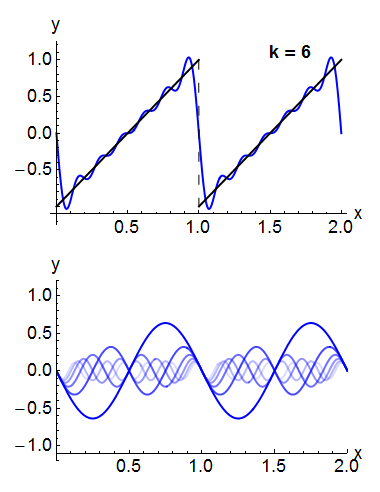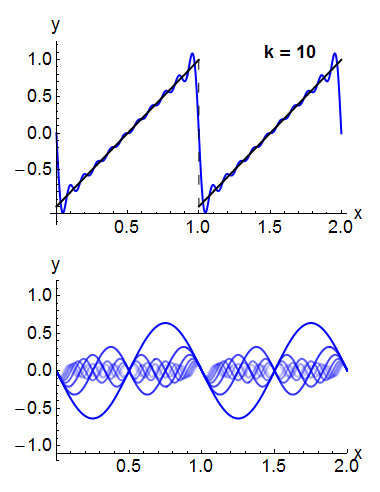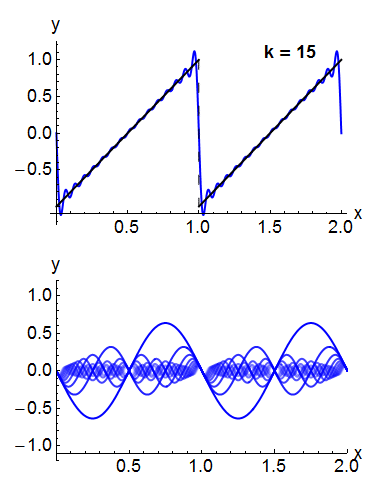
For example, the square wave can be written as the Fourier series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or '' ...
In the animation of a square wave at top right it can be seen that just a few terms already produce a fairly good approximation. The superposition of several terms in the expansion of a sawtooth wave are shown underneath.
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered byHipparchus
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the e ...
of Nicaea
Nicaea, also known as Nicea or Nikaia (; ; grc-gre, Νίκαια, ) was an ancient Greek city in Bithynia, where located in northwestern Anatolia and is primarily known as the site of the First and Second Councils of Nicaea (the first and s ...
(180–125 BCE) and Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importanc ...
of Roman Egypt (90–165 CE). The functions of sine and versine (1 – cosine) can be traced back to the ''jyā'' and ''koti-jyā'' functions used in Gupta period
The Gupta Empire was an ancient Indian empire which existed from the early 4th century CE to late 6th century CE. At its zenith, from approximately 319 to 467 CE, it covered much of the Indian subcontinent. This period is considered as the Gold ...
Indian astronomy
Astronomy has long history in Indian subcontinent stretching from pre-historic to modern times. Some of the earliest roots of Indian astronomy can be dated to the period of Indus Valley civilisation or earlier. Astronomy later developed as a di ...
('' Aryabhatiya'', '' Surya Siddhanta''), via translation from Sanskrit to Arabic and then from Arabic to Latin. (See Aryabhata's sine table.)
All six trigonometric functions in current use were known in Islamic mathematics by the 9th century, as was the law of sines, used in solving triangles Solution of triangles ( la, solutio triangulorum) is the main trigonometric problem of finding the characteristics of a triangle (angles and lengths of sides), when some of these are known. The triangle can be located on a plane or on a sphere. Appl ...
. With the exception of the sine (which was adopted from Indian mathematics), the other five modern trigonometric functions were discovered by Persian and Arab mathematicians, including the cosine, tangent, cotangent, secant and cosecant. Al-Khwārizmī (c. 780–850) produced tables of sines, cosines and tangents. Circa 830, Habash al-Hasib al-Marwazi
Ahmad ibn 'Abdallah Habash Hasib Marwazi (766 - d. after 869 in Samarra, Iraq ) was a north-eastern Iranian astronomer, geographer, and mathematician from Merv in Khorasan who for the first time described the trigonometric ratios: sine, cosine, t ...
discovered the cotangent, and produced tables of tangents and cotangents.Jacques Sesiano, "Islamic mathematics", p. 157, in Muhammad ibn Jābir al-Harrānī al-Battānī
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī aṣ-Ṣābiʾ al-Battānī ( ar, محمد بن جابر بن سنان البتاني) ( Latinized as Albategnius, Albategni or Albatenius) (c. 858 – 929) was an astron ...
(853–929) discovered the reciprocal functions of secant and cosecant, and produced the first table of cosecants for each degree from 1° to 90°. The trigonometric functions were later studied by mathematicians including Omar Khayyám, Bhāskara II, Nasir al-Din al-Tusi, Jamshīd al-Kāshī (14th century), Ulugh Beg (14th century), Regiomontanus (1464), Rheticus, and Rheticus' student Valentinus Otho
Valentinus Otho (also Valentin Otto; born around 1545–46 possibly in Magdeburg – 8 April 1603 in Heidelberg) was a German mathematician and astronomer.
Life
In 1573 he came to Wittenberg, proposing to Johannes Praetorius an approximation o ...
.
Madhava of Sangamagrama (c. 1400) made early strides in the analysis
Analysis ( : analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle (3 ...
of trigonometric functions in terms of infinite series. (See Madhava series
In mathematics, a Madhava series or Leibniz series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by an Indian Mathematician and Astronomer Madhava of Sangamagrama (c.&nbs ...
and Madhava's sine table.)
The tangent function was brought to Europe by Giovanni Bianchini in 1467 in trigonometry tables he created to support the calculation of stellar coordinates.
The terms ''tangent'' and ''secant'' were first introduced by the Danish mathematician Thomas Fincke in his book ''Geometria rotundi'' (1583).
The 17th century French mathematician Albert Girard
Albert Girard () (11 October 1595 in Saint-Mihiel, France − 8 December 1632 in Leiden, The Netherlands) was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and ...
made the first published use of the abbreviations ''sin'', ''cos'', and ''tan'' in his book ''Trigonométrie''.
In a paper published in 1682, Gottfried Leibniz proved that is not an algebraic function of . Though introduced as ratios of sides of a right triangle, and thus appearing to be rational functions, Leibnitz result established that they are actually transcendental function
In mathematics, a transcendental function is an analytic function that does not satisfy a polynomial equation, in contrast to an algebraic function.
In other words, a transcendental function "transcends" algebra in that it cannot be expressed ...
s of their argument. The task of assimilating circular functions into algebraic expressions was accomplished by Euler in his '' Introduction to the Analysis of the Infinite'' (1748). His method was to show that the sine and cosine functions are alternating series formed from the even and odd terms respectively of the exponential series. He presented "Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that ...
", as well as near-modern abbreviations (''sin.'', ''cos.'', ''tang.'', ''cot.'', ''sec.'', and ''cosec.'').
A few functions were common historically, but are now seldom used, such as the chord, the versine (which appeared in the earliest tables), the coversine, the haversine, the exsecant and the excosecant. The list of trigonometric identities shows more relations between these functions.
*
*
*
*
*
*
Etymology
The word derives fromLatin
Latin (, or , ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through ...
'' sinus'', meaning "bend; bay", and more specifically "the hanging fold of the upper part of a toga", "the bosom of a garment", which was chosen as the translation of what was interpreted as the Arabic word ''jaib'', meaning "pocket" or "fold" in the twelfth-century translations of works by Al-Battani
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī aṣ-Ṣābiʾ al-Battānī ( ar, محمد بن جابر بن سنان البتاني) ( Latinized as Albategnius, Albategni or Albatenius) (c. 858 – 929) was an astron ...
and al-Khwārizmī into Medieval Latin
Medieval Latin was the form of Literary Latin used in Roman Catholic Western Europe during the Middle Ages. In this region it served as the primary written language, though local languages were also written to varying degrees. Latin functioned ...
.
The choice was based on a misreading of the Arabic written form ''j-y-b'' (), which itself originated as a transliteration from Sanskrit ', which along with its synonym ' (the standard Sanskrit term for the sine) translates to "bowstring", being in turn adopted from Ancient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic pe ...
"string".
The word ''tangent'' comes from Latin ''tangens'' meaning "touching", since the line ''touches'' the circle of unit radius, whereas ''secant'' stems from Latin ''secans''—"cutting"—since the line ''cuts'' the circle.Oxford English Dictionary
The prefix " co-" (in "cosine", "cotangent", "cosecant") is found in Edmund Gunter's ''Canon triangulorum'' (1620), which defines the ''cosinus'' as an abbreviation for the ''sinus complementi'' (sine of the complementary angle) and proceeds to define the ''cotangens'' similarly.
See also
*All Students Take Calculus
All or ALL may refer to:
Language
* All, an indefinite pronoun in English
* All, one of the English determiners
* Allar language (ISO 639-3 code)
* Allative case (abbreviated ALL)
Music
* All (band), an American punk rock band
* ''All'' (All ...
– a mnemonic for recalling the signs of trigonometric functions in a particular quadrant of a Cartesian plane
* Bhaskara I's sine approximation formula
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I (c. 600 – c. 680), a seventh-century Indian m ...
* Differentiation of trigonometric functions
The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. For example, the derivative of the sine function is written sin� ...
* Generalized trigonometry
Ordinary trigonometry studies triangles in the Euclidean plane . There are a number of ways of defining the ordinary Euclidean geometric trigonometric functions on real numbers, for example right-angled triangle definitions, unit circle defini ...
* Generating trigonometric tables
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tab ...
* Hyperbolic function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the u ...
* List of integrals of trigonometric functions
* List of periodic functions
* List of trigonometric identities
* Polar sine In geometry, the polar sine generalizes the sine function of angle to the vertex angle of a polytope. It is denoted by psin.
Definition
''n'' vectors in ''n''-dimensional space
Let v1, ..., v''n'' (''n'' ≥ 2) be non-z ...
– a generalization to vertex angles
* Proofs of trigonometric identities
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of ...
* Versine – for several less used trigonometric functions
Notes
References
* *Lars Ahlfors
Lars Valerian Ahlfors (18 April 1907 – 11 October 1996) was a Finnish mathematician, remembered for his work in the field of Riemann surfaces and his text on complex analysis.
Background
Ahlfors was born in Helsinki, Finland. His mother, Si ...
, ''Complex Analysis: an introduction to the theory of analytic functions of one complex variable'', second edition, McGraw-Hill Book Company, New York, 1966.
* Boyer, Carl B., ''A History of Mathematics'', John Wiley & Sons, Inc., 2nd edition. (1991). .
*
* Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).
* Joseph, George G., ''The Crest of the Peacock: Non-European Roots of Mathematics'', 2nd ed. Penguin Books
Penguin Books is a British publishing, publishing house. It was co-founded in 1935 by Allen Lane with his brothers Richard and John, as a line of the publishers The Bodley Head, only becoming a separate company the following year.Trigonometric Delights
', Princeton Univ. Press. (1998). Reprint edition (2002): . * Needham, Tristan
"Preface"
to
Visual Complex Analysis
'. Oxford University Press, (1999). . * * O'Connor, J. J., and E. F. Robertson
'' MacTutor History of Mathematics archive''. (1996). * O'Connor, J. J., and E. F. Robertson
"Madhava of Sangamagramma"
'' MacTutor History of Mathematics archive''. (2000). * Pearce, Ian G.
"Madhava of Sangamagramma"
, '' MacTutor History of Mathematics archive''. (2002). * * Weisstein, Eric W.
"Tangent"
from '' MathWorld'', accessed 21 January 2006.
Visionlearning Module on Wave Mathematics
GonioLab
Visualization of the unit circle, trigonometric and hyperbolic functions
Article about the q-analog of sin at MathWorld
q-Cosine
Article about the q-analog of cos at MathWorld {{DEFAULTSORT:Trigonometric Functions Angle Trigonometry Elementary special functions Analytic functions Ratios Dimensionless numbers
', Princeton Univ. Press. (1998). Reprint edition (2002): . * Needham, Tristan
"Preface"
to
Visual Complex Analysis
'. Oxford University Press, (1999). . * * O'Connor, J. J., and E. F. Robertson
'' MacTutor History of Mathematics archive''. (1996). * O'Connor, J. J., and E. F. Robertson
"Madhava of Sangamagramma"
'' MacTutor History of Mathematics archive''. (2000). * Pearce, Ian G.
"Madhava of Sangamagramma"
, '' MacTutor History of Mathematics archive''. (2002). * * Weisstein, Eric W.
"Tangent"
from '' MathWorld'', accessed 21 January 2006.
External links
*Visionlearning Module on Wave Mathematics
GonioLab
Visualization of the unit circle, trigonometric and hyperbolic functions
Article about the q-analog of sin at MathWorld
q-Cosine
Article about the q-analog of cos at MathWorld {{DEFAULTSORT:Trigonometric Functions Angle Trigonometry Elementary special functions Analytic functions Ratios Dimensionless numbers