torus group on:
[Wikipedia]
[Google]
[Amazon]
 In
In
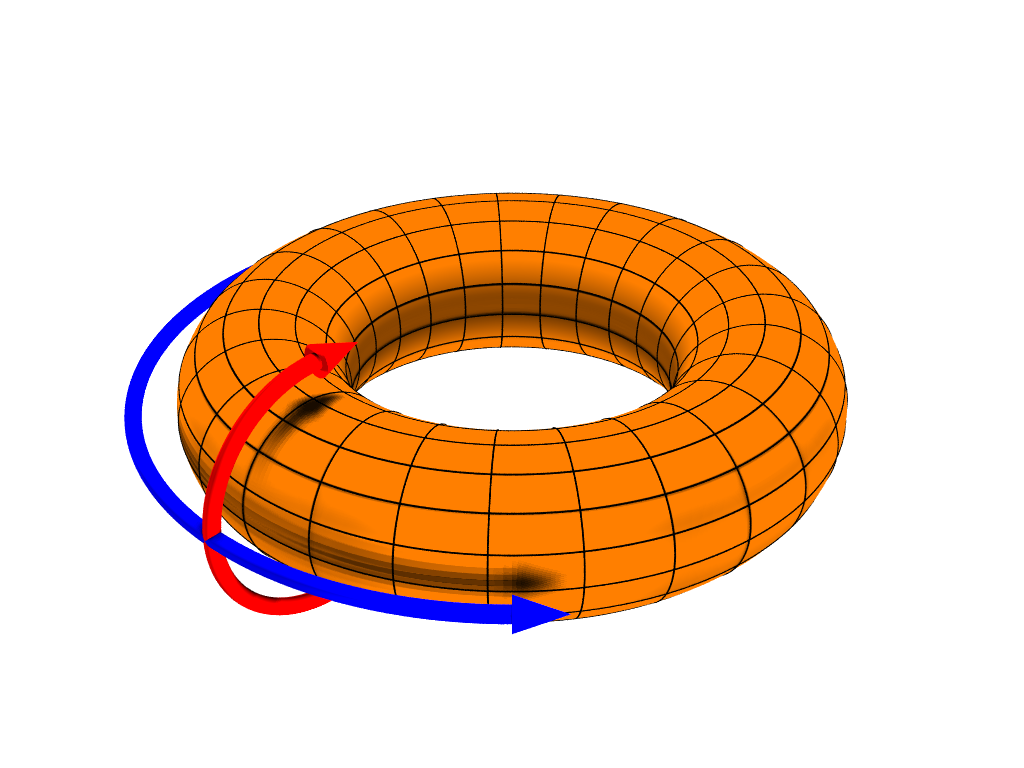 A torus of revolution in 3-space can be parametrized as:
using angular coordinates , , representing rotation around the tube and rotation around the torus's axis of revolution, respectively, where the ''major radius'' is the distance from the center of the tube to the center of the torus and the ''minor radius'' is the radius of the tube.
The ratio is called the ''
A torus of revolution in 3-space can be parametrized as:
using angular coordinates , , representing rotation around the tube and rotation around the torus's axis of revolution, respectively, where the ''major radius'' is the distance from the center of the tube to the center of the torus and the ''minor radius'' is the radius of the tube.
The ratio is called the ''
 The torus has a generalization to higher dimensions, the , often called the or for short. (This is the more typical meaning of the term "-torus", the other referring to holes or of genus .) Just as the ordinary torus is topologically the product space of two circles, the -dimensional torus is ''topologically equivalent to'' the product of circles. That is:
:
The standard 1-torus is just the circle: . The torus discussed above is the standard 2-torus, . And similar to the 2-torus, the -torus, can be described as a quotient of under integral shifts in any coordinate. That is, the ''n''-torus is modulo the action of the integer lattice (with the action being taken as vector addition). Equivalently, the -torus is obtained from the -dimensional
The torus has a generalization to higher dimensions, the , often called the or for short. (This is the more typical meaning of the term "-torus", the other referring to holes or of genus .) Just as the ordinary torus is topologically the product space of two circles, the -dimensional torus is ''topologically equivalent to'' the product of circles. That is:
:
The standard 1-torus is just the circle: . The torus discussed above is the standard 2-torus, . And similar to the 2-torus, the -torus, can be described as a quotient of under integral shifts in any coordinate. That is, the ''n''-torus is modulo the action of the integer lattice (with the action being taken as vector addition). Equivalently, the -torus is obtained from the -dimensional
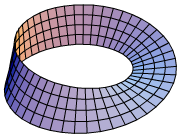
 As the -torus is the -fold product of the circle, the -torus is the configuration space of ordered, not necessarily distinct points on the circle. Symbolically, . The configuration space of ''unordered'', not necessarily distinct points is accordingly the
As the -torus is the -fold product of the circle, the -torus is the configuration space of ordered, not necessarily distinct points on the circle. Symbolically, . The configuration space of ''unordered'', not necessarily distinct points is accordingly the

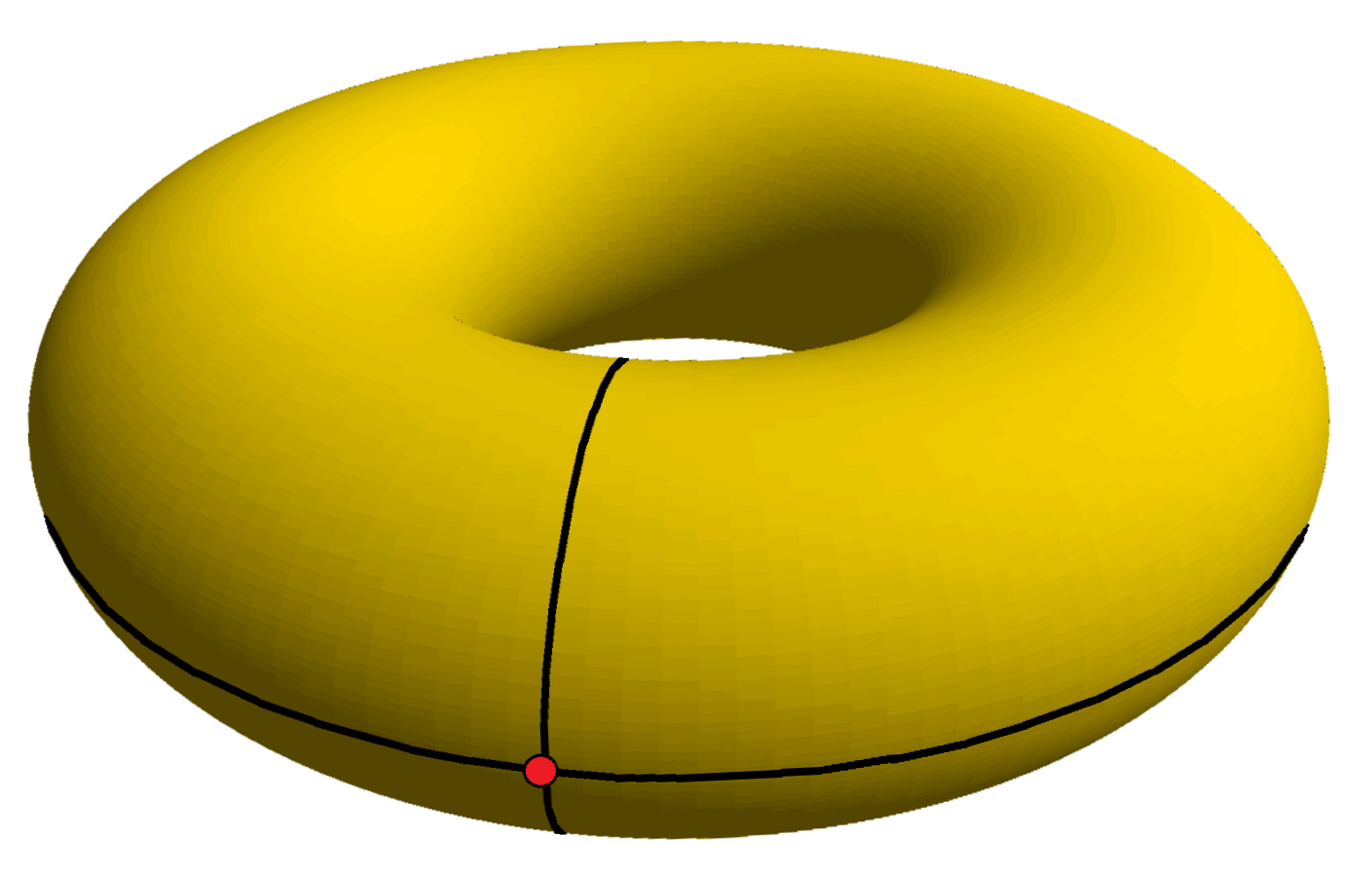 A flat torus is a torus with the metric inherited from its representation as the
A flat torus is a torus with the metric inherited from its representation as the  In April 2012, an explicit ''C''1 (continuously differentiable) isometric embedding of a flat torus into 3-dimensional Euclidean space was found. It is a flat torus in the sense that, as a metric space, it is isometric to a flat square torus. It is similar in structure to a
In April 2012, an explicit ''C''1 (continuously differentiable) isometric embedding of a flat torus into 3-dimensional Euclidean space was found. It is a flat torus in the sense that, as a metric space, it is isometric to a flat square torus. It is similar in structure to a


''Algebraic Topology''
Cambridge University Press, 2002. . * V. V. Nikulin, I. R. Shafarevich. ''Geometries and Groups''. Springer, 1987. , .
"Tore (notion géométrique)" at ''Encyclopédie des Formes Mathématiques Remarquables''
Creation of a torus
at
"4D torus"
Fly-through cross-sections of a four-dimensional torus
"Relational Perspective Map"
Visualizing high dimensional data with flat torus
* Archived a
Ghostarchive
and th
Wayback Machine
* {{Authority control Surfaces
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a torus (: tori or toruses) is a surface of revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersec ...
generated by revolving a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
in three-dimensional space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three- ...
one full revolution about an axis that is coplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. How ...
with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.
If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
. If the revolved curve is not a circle, the surface is called a ''toroid
In mathematics, a toroid is a surface of revolution with a hole in the middle. The axis of revolution passes through the hole and so does not intersect the surface. For example, when a rectangle is rotated around an axis parallel to one of its ...
'', as in a square toroid.
Real-world objects that approximate a torus of revolution include swim rings, inner tube
An inner tube is an inflatable torus that forms the interior of some pneumatic tires. The tube is inflated through a valve stem and fits inside the tire casing. The inflated inner tube provides structural support and suspension, while the out ...
s and ringette rings.
A torus should not be confused with a ''solid torus
In mathematics, a solid torus is the topological space formed by sweeping a disk around a circle. It is homeomorphic to the Cartesian product S^1 \times D^2 of the disk and the circle, endowed with the product topology.
A standard way to visual ...
'', which is formed by rotating a disk, rather than a circle, around an axis. A solid torus is a torus plus the volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
inside the torus. Real-world objects that approximate a ''solid torus'' include O-ring
An O-ring, also known as a packing or a toric joint, is a mechanical gasket in the shape of a torus; it is a loop of elastomer with a round cross section (geometry), cross-section, designed to be seated in a groove and compressed during assembl ...
s, non-inflatable lifebuoys, ring doughnut
A doughnut or donut () is a type of pastry made from leavened fried dough. It is popular in many countries and is prepared in various forms as a sweet snack that can be homemade or purchased in bakeries, supermarkets, food stalls, and fran ...
s, and bagel
A bagel (; ; also spelled beigel) is a bread roll originating in the Jewish communities of Poland. Bagels are traditionally made from yeasted wheat dough that is shaped by hand into a torus or ring, briefly boiled in water, and then baked. ...
s.
In topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, a ring torus is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
to the Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets and , denoted , is the set of all ordered pairs where is an element of and is an element of . In terms of set-builder notation, that is
A\times B = \.
A table c ...
of two circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
s: , and the latter is taken to be the definition in that context. It is a compact 2-manifold of genus 1. The ring torus is one way to embed this space into Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, but another way to do this is the Cartesian product of the embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup.
When some object X is said to be embedded in another object Y ...
of in the plane with itself. This produces a geometric object called the Clifford torus
In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the Cartesian product of two circles and (in the same sense that the surface of a cylinder is "flat"). It is named after William Kingdon Cliffo ...
, a surface in 4-space.
In the field of topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, a torus is any topological space that is homeomorphic to a torus. The surface of a coffee cup and a doughnut are both topological tori with genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
one.
An example of a torus can be constructed by taking a rectangular strip of flexible material such as rubber, and joining the top edge to the bottom edge, and the left edge to the right edge, without any half-twists (compare Klein bottle
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the ...
).
Etymology
''Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
'' is a Latin word denoting something round, a swelling, an elevation, a protuberance.
Geometry
 A torus of revolution in 3-space can be parametrized as:
using angular coordinates , , representing rotation around the tube and rotation around the torus's axis of revolution, respectively, where the ''major radius'' is the distance from the center of the tube to the center of the torus and the ''minor radius'' is the radius of the tube.
The ratio is called the ''
A torus of revolution in 3-space can be parametrized as:
using angular coordinates , , representing rotation around the tube and rotation around the torus's axis of revolution, respectively, where the ''major radius'' is the distance from the center of the tube to the center of the torus and the ''minor radius'' is the radius of the tube.
The ratio is called the ''aspect ratio
The aspect ratio of a geometry, geometric shape is the ratio of its sizes in different dimensions. For example, the aspect ratio of a rectangle is the ratio of its longer side to its shorter side—the ratio of width to height, when the rectangl ...
'' of the torus. The typical doughnut confectionery has an aspect ratio of about 3 to 2.
An implicit equation in Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
for a torus radially symmetric about the z-axis
An axis (: axes) may refer to:
Mathematics
*A specific line (often a directed line) that plays an important role in some contexts. In particular:
** Coordinate axis of a coordinate system
*** ''x''-axis, ''y''-axis, ''z''-axis, common names ...
is
Algebraically eliminating the square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
gives a quartic equation
In mathematics, a quartic equation is one which can be expressed as a ''quartic function'' equaling zero. The general form of a quartic equation is
:ax^4+bx^3+cx^2+dx+e=0 \,
where ''a'' ≠ 0.
The quartic is the highest order polynom ...
,
The three classes of standard tori correspond to the three possible aspect ratios between and :
* When , the surface will be the familiar ring torus or anchor ring.
* corresponds to the horn torus, which in effect is a torus with no "hole".
* describes the self-intersecting spindle torus; its inner shell is a ''lemon
The lemon (''Citrus'' × ''limon'') is a species of small evergreen tree in the ''Citrus'' genus of the flowering plant family Rutaceae. A true lemon is a hybrid of the citron and the bitter orange. Its origins are uncertain, but some ...
'' and its outer shell is an ''apple
An apple is a round, edible fruit produced by an apple tree (''Malus'' spp.). Fruit trees of the orchard or domestic apple (''Malus domestica''), the most widely grown in the genus, are agriculture, cultivated worldwide. The tree originated ...
''.
* When , the torus degenerates to the sphere radius .
* When , the torus degenerates to the circle radius .
When , the interior
of this torus is diffeomorphic
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
Defini ...
(and, hence, homeomorphic) to a product of a Euclidean open disk and a circle. The volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
of this solid torus and the surface area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the d ...
of its torus are easily computed using Pappus's centroid theorem, giving:
These formulae are the same as for a cylinder of length and radius , obtained from cutting the tube along the plane of a small circle, and unrolling it by straightening out (rectifying) the line running around the center of the tube. The losses in surface area and volume on the inner side of the tube exactly cancel out the gains on the outer side.
Expressing the surface area and the volume by the distance of an outermost point on the surface of the torus to the center, and the distance of an innermost point to the center (so that and ), yields
As a torus is the product of two circles, a modified version of the spherical coordinate system
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
is sometimes used.
In traditional spherical coordinates there are three measures, , the distance from the center of the coordinate system, and and , angles measured from the center point.
As a torus has, effectively, two center points, the centerpoints of the angles are moved; measures the same angle as it does in the spherical system, but is known as the "toroidal" direction. The center point of is moved to the center of , and is known as the "poloidal" direction. These terms were first used in a discussion of the Earth's magnetic field, where "poloidal" was used to denote "the direction toward the poles".
In modern use, toroidal and poloidal
The terms toroidal and poloidal refer to directions relative to a torus of reference. They describe a three-dimensional coordinate system in which the poloidal direction follows a small circular ring around the surface, while the toroidal direct ...
are more commonly used to discuss magnetic confinement fusion
Magnetic confinement fusion (MCF) is an approach to generate thermonuclear fusion power that uses magnetic fields to confine fusion fuel in the form of a plasma (physics), plasma. Magnetic confinement is one of two major branches of controlled fusi ...
devices.
Topology
Topologically, a torus is a closed surface defined as the product of twocircle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
s: . This can be viewed as lying in and is a subset of the 3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior o ...
of radius . This topological torus is also often called the Clifford torus
In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the Cartesian product of two circles and (in the same sense that the surface of a cylinder is "flat"). It is named after William Kingdon Cliffo ...
. In fact, is filled out by a family of nested tori in this manner (with two degenerate circles), a fact that is important in the study of as a fiber bundle
In mathematics, and particularly topology, a fiber bundle ( ''Commonwealth English'': fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a pr ...
over (the Hopf bundle).
The surface described above, given the relative topology
Relative may refer to:
General use
*Kinship and family, the principle binding the most basic social units of society. If two people are connected by circumstances of birth, they are said to be ''relatives''.
Philosophy
* Relativism, the concept ...
from , is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
to a topological torus as long as it does not intersect its own axis. A particular homeomorphism is given by stereographically projecting the topological torus into from the north pole of .
The torus can also be described as a quotient
In arithmetic, a quotient (from 'how many times', pronounced ) is a quantity produced by the division of two numbers. The quotient has widespread use throughout mathematics. It has two definitions: either the integer part of a division (in th ...
of the Cartesian plane
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
under the identifications
:
or, equivalently, as the quotient of the unit square
In mathematics, a unit square is a square whose sides have length . Often, ''the'' unit square refers specifically to the square in the Cartesian plane with corners at the four points ), , , and .
Cartesian coordinates
In a Cartesian coordinat ...
by pasting the opposite edges together, described as a fundamental polygon
In mathematics, a fundamental polygon can be defined for every compact Riemann surface of genus greater than 0. It encodes not only information about the topology of the surface through its fundamental group but also determines the Riemann surfa ...
.
The fundamental group
In the mathematics, mathematical field of algebraic topology, the fundamental group of a topological space is the group (mathematics), group of the equivalence classes under homotopy of the Loop (topology), loops contained in the space. It record ...
of the torus is just the direct product
In mathematics, a direct product of objects already known can often be defined by giving a new one. That induces a structure on the Cartesian product of the underlying sets from that of the contributing objects. The categorical product is an abs ...
of the fundamental group of the circle with itself:
:
Intuitively speaking, this means that a closed path that circles the torus's "hole" (say, a circle that traces out a particular latitude) and then circles the torus's "body" (say, a circle that traces out a particular longitude) can be deformed to a path that circles the body and then the hole. So, strictly 'latitudinal' and strictly 'longitudinal' paths commute. An equivalent statement may be imagined as two shoelaces passing through each other, then unwinding, then rewinding.
The fundamental group can also be derived from taking the torus as the quotient (see below), so that may be taken as its universal cover
In topology, a covering or covering projection is a map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphism ...
, with deck transformation group .
Its higher homotopy groups
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about Loop (topology), loops in a Mathematic ...
are all trivial, since a universal cover projection always induces isomorphisms between the groups and for , and is contractible
In mathematics, a topological space ''X'' is contractible if the identity map on ''X'' is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point within t ...
.
The torus has homology groups
Thus, the first homology group of the torus is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
to its fundamental group-- which in particular can be deduced from Hurewicz theorem
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism. The theorem is named after Witold Hurewicz, and generalizes earlier results ...
since is abelian.
The cohomology groups with integer coefficients are isomorphic to the homology ones-- which can be seen either by direct computation, the universal coefficient theorem or even Poincaré duality
In mathematics, the Poincaré duality theorem, named after Henri Poincaré, is a basic result on the structure of the homology (mathematics), homology and cohomology group (mathematics), groups of manifolds. It states that if ''M'' is an ''n''-dim ...
.
If a torus is punctured and turned inside out then another torus results, with lines of latitude and longitude interchanged. This is equivalent to building a torus from a cylinder, by joining the circular ends together, in two ways: around the outside like joining two ends of a garden hose, or through the inside like rolling a sock (with the toe cut off). Additionally, if the cylinder was made by gluing two opposite sides of a rectangle together, choosing the other two sides instead will cause the same reversal of orientation.
Two-sheeted cover
The 2-torus is a twofold branched cover of the 2-sphere, with four ramification points. Everyconformal structure
In mathematics, conformal geometry is the study of the set of angle-preserving (conformal map, conformal) transformations on a space.
In a real two dimensional space, conformal geometry is precisely the geometry of Riemann surfaces. In space highe ...
on the 2-torus can be represented as such a two-sheeted cover of the 2-sphere. The points on the torus corresponding to the ramification points are the Weierstrass points. In fact, the conformal type of the torus is determined by the cross-ratio
In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points , , , on a line, their cross ratio is defin ...
of the four points.
''n''-dimensional torus
 The torus has a generalization to higher dimensions, the , often called the or for short. (This is the more typical meaning of the term "-torus", the other referring to holes or of genus .) Just as the ordinary torus is topologically the product space of two circles, the -dimensional torus is ''topologically equivalent to'' the product of circles. That is:
:
The standard 1-torus is just the circle: . The torus discussed above is the standard 2-torus, . And similar to the 2-torus, the -torus, can be described as a quotient of under integral shifts in any coordinate. That is, the ''n''-torus is modulo the action of the integer lattice (with the action being taken as vector addition). Equivalently, the -torus is obtained from the -dimensional
The torus has a generalization to higher dimensions, the , often called the or for short. (This is the more typical meaning of the term "-torus", the other referring to holes or of genus .) Just as the ordinary torus is topologically the product space of two circles, the -dimensional torus is ''topologically equivalent to'' the product of circles. That is:
:
The standard 1-torus is just the circle: . The torus discussed above is the standard 2-torus, . And similar to the 2-torus, the -torus, can be described as a quotient of under integral shifts in any coordinate. That is, the ''n''-torus is modulo the action of the integer lattice (with the action being taken as vector addition). Equivalently, the -torus is obtained from the -dimensional hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
by gluing the opposite faces together.
An -torus in this sense is an example of an ''n-''dimensional compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
. It is also an example of a compact abelian Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
. This follows from the fact that the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
is a compact abelian Lie group (when identified with the unit complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s with multiplication). Group multiplication on the torus is then defined by coordinate-wise multiplication.
Toroidal groups play an important part in the theory of compact Lie group
In mathematics, a compact (topological) group is a topological group whose topology realizes it as a compact space, compact topological space (when an element of the group is operated on, the result is also within the group). Compact groups are ...
s. This is due in part to the fact that in any compact Lie group one can always find a maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.
A torus in a compact Lie group ''G'' is a compact, connected, abelian Lie subgroup of ''G'' (and therefor ...
; that is, a closed subgroup
In group theory, a branch of mathematics, a subset of a group G is a subgroup of G if the members of that subset form a group with respect to the group operation in G.
Formally, given a group (mathematics), group under a binary operation ...
which is a torus of the largest possible dimension. Such maximal tori have a controlling role to play in theory of connected . Toroidal groups are examples of protori, which (like tori) are compact connected abelian groups, which are not required to be manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
s.
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphism ...
s of are easily constructed from automorphisms of the lattice , which are classified by invertible
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
integral matrices In mathematics, an integer matrix is a matrix whose entries are all integers. Examples include binary matrices, the zero matrix, the matrix of ones, the identity matrix, and the adjacency matrices used in graph theory, amongst many others. Integ ...
of size with an integral inverse; these are just the integral matrices with determinant . Making them act on in the usual way, one has the typical ''toral automorphism'' on the quotient.
The fundamental group
In the mathematics, mathematical field of algebraic topology, the fundamental group of a topological space is the group (mathematics), group of the equivalence classes under homotopy of the Loop (topology), loops contained in the space. It record ...
of an ''n''-torus is a free abelian group
In mathematics, a free abelian group is an abelian group with a Free module, basis. Being an abelian group means that it is a Set (mathematics), set with an addition operation (mathematics), operation that is associative, commutative, and inverti ...
of rank . The th homology group
In mathematics, the term homology, originally introduced in algebraic topology, has three primary, closely-related usages. The most direct usage of the term is to take the ''homology of a chain complex'', resulting in a sequence of abelian grou ...
of an -torus is a free abelian group of rank ''n'' choose . It follows that the Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's ...
of the -torus is for all . The cohomology ring In mathematics, specifically algebraic topology, the cohomology ring of a topological space ''X'' is a ring formed from the cohomology groups of ''X'' together with the cup product serving as the ring multiplication. Here 'cohomology' is usually un ...
''H''•(, Z) can be identified with the exterior algebra
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
over the - module whose generators are the duals of the nontrivial cycles.
Configuration space

orbifold
In the mathematical disciplines of topology and geometry, an orbifold (for "orbit-manifold") is a generalization of a manifold. Roughly speaking, an orbifold is a topological space that is locally a finite group quotient of a Euclidean space.
D ...
, which is the quotient of the torus by the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric grou ...
on letters (by permuting the coordinates).
For , the quotient is the Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
, the edge corresponding to the orbifold points where the two coordinates coincide. For this quotient may be described as a solid torus with cross-section an equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
, with a twist; equivalently, as a triangular prism
In geometry, a triangular prism or trigonal prism is a Prism (geometry), prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a ''right triangular prism''. A right triangul ...
whose top and bottom faces are connected with a 1/3 twist (120°): the 3-dimensional interior corresponds to the points on the 3-torus where all 3 coordinates are distinct, the 2-dimensional face corresponds to points with 2 coordinates equal and the 3rd different, while the 1-dimensional edge corresponds to points with all 3 coordinates identical.
These orbifolds have found significant applications to music theory in the work of Dmitri Tymoczko and collaborators (Felipe Posada, Michael Kolinas, et al.), being used to model musical triads.
Flat torus

 A flat torus is a torus with the metric inherited from its representation as the
A flat torus is a torus with the metric inherited from its representation as the quotient
In arithmetic, a quotient (from 'how many times', pronounced ) is a quantity produced by the division of two numbers. The quotient has widespread use throughout mathematics. It has two definitions: either the integer part of a division (in th ...
, , where is a discrete subgroup of isomorphic to . This gives the quotient the structure of a Riemannian manifold
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the N-sphere, n-sphere, hyperbolic space, and smooth surf ...
, as well as the structure of an abelian Lie group. Perhaps the simplest example of this is when : , which can also be described as the Cartesian plane
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
under the identifications . This particular flat torus (and any uniformly scaled version of it) is known as the "square" flat torus.
This metric of the square flat torus can also be realised by specific embeddings of the familiar 2-torus into Euclidean 4-space or higher dimensions. Its surface has zero Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
everywhere. It is flat in the same sense that the surface of a cylinder is flat. In 3 dimensions, one can bend a flat sheet of paper into a cylinder without stretching the paper, but this cylinder cannot be bent into a torus without stretching the paper (unless some regularity and differentiability conditions are given up, see below).
A simple 4-dimensional Euclidean embedding of a rectangular flat torus (more general than the square one) is as follows:
:
where ''R'' and ''P'' are positive constants determining the aspect ratio. It is diffeomorphic
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
Defini ...
to a regular torus but not isometric. It can not be analytically embedded ( smooth of class ) into Euclidean 3-space. Mapping it into ''3''-space requires one to stretch it, in which case it looks like a regular torus. For example, in the following map:
:
If and in the above flat torus parametrization form a unit vector then ''u'', ''v'', and parameterize the unit 3-sphere as Hopf coordinates. In particular, for certain very specific choices of a square flat torus in the 3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior o ...
''S''3, where above, the torus will partition the 3-sphere into two congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
solid tori subsets with the aforesaid flat torus surface as their common boundary. One example is the torus defined by
:
Other tori in having this partitioning property include the square tori of the form , where is a rotation of 4-dimensional space , or in other words is a member of the Lie group .
It is known that there exists no (twice continuously differentiable) embedding of a flat torus into 3-space. (The idea of the proof is to take a large sphere containing such a flat torus in its interior, and shrink the radius of the sphere until it just touches the torus for the first time. Such a point of contact must be a tangency. But that would imply that part of the torus, since it has zero curvature everywhere, must lie strictly outside the sphere, which is a contradiction.) On the other hand, according to the Nash-Kuiper theorem, which was proven in the 1950s, an isometric ''C''1 embedding exists. This is solely an existence proof and does not provide explicit equations for such an embedding.
 In April 2012, an explicit ''C''1 (continuously differentiable) isometric embedding of a flat torus into 3-dimensional Euclidean space was found. It is a flat torus in the sense that, as a metric space, it is isometric to a flat square torus. It is similar in structure to a
In April 2012, an explicit ''C''1 (continuously differentiable) isometric embedding of a flat torus into 3-dimensional Euclidean space was found. It is a flat torus in the sense that, as a metric space, it is isometric to a flat square torus. It is similar in structure to a fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
as it is constructed by repeatedly corrugating an ordinary torus at smaller scales. Like fractals, it has no defined Gaussian curvature. However, unlike fractals, it does have defined surface normals
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the c ...
, yielding a so-called "smooth fractal". The key to obtaining the smoothness of this corrugated torus is to have the amplitudes of successive corrugations decreasing faster than their "wavelengths". (These infinitely recursive corrugations are used only for embedding into three dimensions; they are not an intrinsic feature of the flat torus.) This is the first time that any such embedding was defined by explicit equations or depicted by computer graphics.
Conformal classification of flat tori
In the study ofRiemann surfaces
In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed vers ...
, one says that any two smooth compact geometric surfaces are "conformally equivalent" when there exists a smooth homeomorphism between them that is both angle-preserving and orientation-preserving. The Uniformization theorem
In mathematics, the uniformization theorem states that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generali ...
guarantees that every Riemann surface is conformally equivalent to one that has constant Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
. In the case of a torus, the constant curvature must be zero. Then one defines the "moduli space
In mathematics, in particular algebraic geometry, a moduli space is a geometric space (usually a scheme (mathematics), scheme or an algebraic stack) whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of suc ...
" of the torus to contain one point for each conformal equivalence class, with the appropriate topology. It turns out that this moduli space ''M'' may be identified with a punctured sphere that is smooth except for two points that have less angle than 2π (radians) around them: One has total angle π and the other has total angle 2π/3.
''M'' may be turned into a compact space ''M*'' – topologically equivalent to a sphere – by adding one additional point that represents the limiting case as a rectangular torus approaches an aspect ratio of 0 in the limit. The result is that this compactified moduli space is a sphere with ''three'' points each having less than 2π total angle around them. (Such a point is termed a "cusp", and may be thought of as the vertex of a cone, also called a "conepoint".) This third conepoint will have zero total angle around it. Due to symmetry, ''M*'' may be constructed by glueing together two congruent geodesic triangle
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conne ...
s in the hyperbolic plane along their (identical) boundaries, where each triangle has angles of , , and . (The three angles of a hyperbolic triangle T determine T up to congruence.) As a result, the Gauss–Bonnet theorem shows that the area of each triangle can be calculated as , so it follows that the compactified moduli space ''M*'' has area equal to .
The other two cusps occur at the points corresponding in ''M*'' to (a) the square torus (total angle ) and (b) the hexagonal torus (total angle ). These are the only conformal equivalence classes of flat tori that have any conformal automorphisms other than those generated by translations and negation.
Genus ''g'' surface
In the theory ofsurface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
s there is a more general family of objects, the "genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
" surfaces. A genus surface is the connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classifi ...
of two-tori. (And so the torus itself is the surface of genus 1.) To form a connected sum of two surfaces, remove from each the interior of a disk and "glue" the surfaces together along the boundary circles. (That is, merge the two boundary circles so they become just one circle.) To form the connected sum of more than two surfaces, successively take the connected sum of two of them at a time until they are all connected. In this sense, a genus surface resembles the surface of doughnuts stuck together side by side, or a 2-sphere
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center' ...
with handles attached.
As examples, a genus zero surface (without boundary) is the two-sphere
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center ...
while a genus one surface (without boundary) is the ordinary torus. The surfaces of higher genus are sometimes called -holed tori (or, rarely, -fold tori). The terms double torus and triple torus are also occasionally used.
The classification theorem for surfaces states that every compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
connected surface is topologically equivalent to either the sphere or the connect sum of some number of tori, disks, and real projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
s.
Toroidal polyhedra
Polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
with the topological type of a torus are called toroidal polyhedra, and have Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's ...
. For any number of holes, the formula generalizes to , where is the number of holes.
The term "toroidal polyhedron" is also used for higher-genus polyhedra and for immersions of toroidal polyhedra.
Automorphisms
Thehomeomorphism group In mathematics, particularly topology, the homeomorphism group of a topological space is the group consisting of all homeomorphisms from the space to itself with function composition as the group operation. They are important to the theory of top ...
(or the subgroup of diffeomorphisms) of the torus is studied in geometric topology
In mathematics, geometric topology is the study of manifolds and Map (mathematics)#Maps as functions, maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topo ...
. Its mapping class group
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
Mo ...
(the connected components of the homeomorphism group) is surjective onto the group of invertible integer matrices, which can be realized as linear maps on the universal covering space that preserve the standard lattice (this corresponds to integer coefficients) and thus descend to the quotient.
At the level of homotopy
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. ...
and homology, the mapping class group can be identified as the action on the first homology (or equivalently, first cohomology, or on the fundamental group
In the mathematics, mathematical field of algebraic topology, the fundamental group of a topological space is the group (mathematics), group of the equivalence classes under homotopy of the Loop (topology), loops contained in the space. It record ...
, as these are all naturally isomorphic; also the first cohomology group
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed ...
generates the cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed ...
algebra:
:
Since the torus is an Eilenberg–MacLane space
In mathematics, specifically algebraic topology, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without a space), and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. ...
, its homotopy equivalences, up to homotopy, can be identified with automorphisms of the fundamental group); all homotopy equivalences of the torus can be realized by homeomorphisms – every homotopy equivalence is homotopic to a homeomorphism.
Thus the short exact sequence
In mathematics, an exact sequence is a sequence of morphisms between objects (for example, Group (mathematics), groups, Ring (mathematics), rings, Module (mathematics), modules, and, more generally, objects of an abelian category) such that the Im ...
of the mapping class group splits (an identification of the torus as the quotient of gives a splitting, via the linear maps, as above):
:
The mapping class group of higher genus surfaces is much more complicated, and an area of active research.
Coloring a torus
The torus's Heawood number is seven, meaning every graph that can be embedded on the torus has achromatic number
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring i ...
of at most seven. (Since the complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices i ...
can be embedded on the torus, and , the upper bound is tight.) Equivalently, in a torus divided into regions, it is always possible to color the regions using no more than seven colors so that no neighboring regions are the same color. (Contrast with the four color theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions shar ...
for the plane.)

de Bruijn torus
Incombinatorial
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ...
mathematics, a ''de Bruijn torus'' is an array of symbols from an alphabet (often just 0 and 1) that contains every -by- matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
exactly once. It is a torus because the edges are considered wraparound for the purpose of finding matrices. Its name comes from the De Bruijn sequence, which can be considered a special case where is 1 (one dimension).
Cutting a torus
A solid torus of revolution can be cut by ''n'' (> 0) planes into at most : parts. (This assumes the pieces may not be rearranged but must remain in place for all cuts.) The first 11 numbers of parts, for (including the case of , not covered by the above formulas), are as follows: : 1, 2, 6, 13, 24, 40, 62, 91, 128, 174, 230, ... .See also
Notes
* ''Nociones de Geometría Analítica y Álgebra Lineal'', , Author: Kozak Ana Maria, Pompeya Pastorelli Sonia, Verdanega Pedro Emilio, Editorial: McGraw-Hill, Edition 2007, 744 pages, language: Spanish * Allen Hatcher''Algebraic Topology''
Cambridge University Press, 2002. . * V. V. Nikulin, I. R. Shafarevich. ''Geometries and Groups''. Springer, 1987. , .
"Tore (notion géométrique)" at ''Encyclopédie des Formes Mathématiques Remarquables''
References
External links
Creation of a torus
at
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow ...
"4D torus"
Fly-through cross-sections of a four-dimensional torus
"Relational Perspective Map"
Visualizing high dimensional data with flat torus
* Archived a
Ghostarchive
and th
Wayback Machine
* {{Authority control Surfaces