Torsion Of A Curve on:
[Wikipedia]
[Google]
[Amazon]
In the differential geometry of curves in
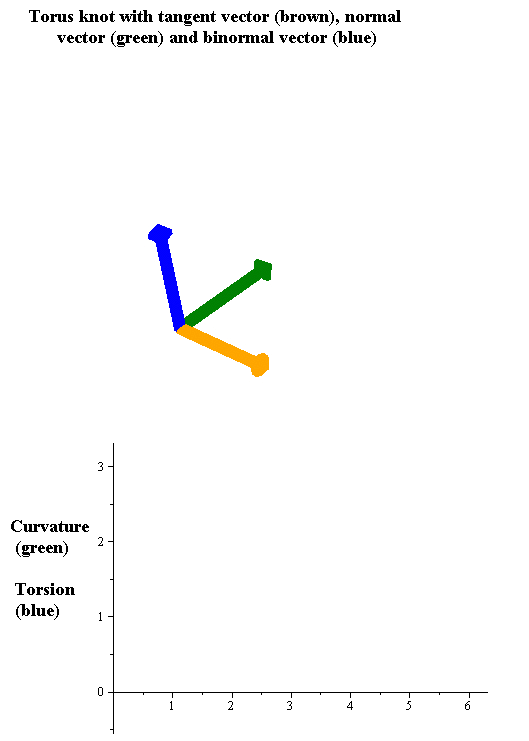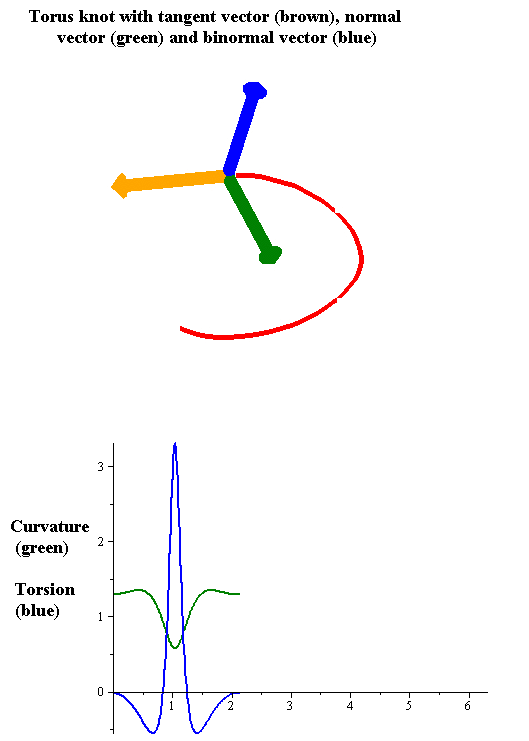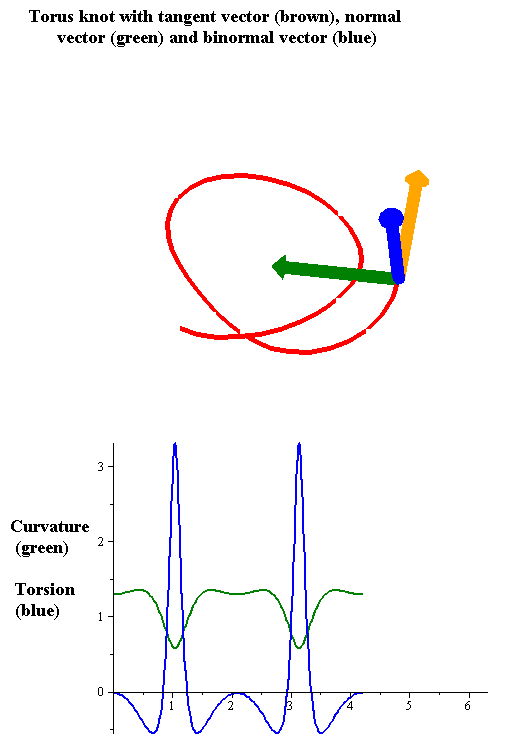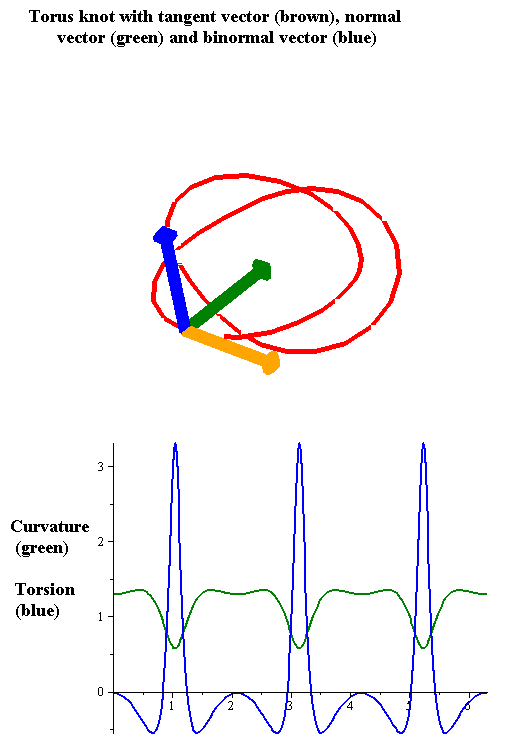 Let be a
Let be a
three dimensions
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called '' parameters'') are required to determine the position of an element (i.e., point). This is the inform ...
, the torsion of a curve measures how sharply it is twisting out of the osculating plane {{Unreferenced, date=May 2019, bot=noref (GreenC bot)
In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a secon ...
. Taken together, the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
and the torsion of a space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, ...
s for the Frenet frame given by the Frenet–Serret formulas.
Definition
 Let be a
Let be a space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
parametrized by arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
and with the unit tangent vector
Unit may refer to:
Arts and entertainment
* UNIT, a fictional military organization in the science fiction television series ''Doctor Who''
* Unit of action, a discrete piece of action (or beat) in a theatrical presentation
Music
* ''Unit'' (al ...
. If the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
of at a certain point is not zero then the principal normal vector
Principal may refer to:
Title or rank
* Principal (academia), the chief executive of a university
** Principal (education), the office holder/ or boss in any school
* Principal (civil service) or principal officer, the senior management level ...
and the binormal vector at that point are the unit vectors
:
respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation
:
which means
:
As , this is equivalent to .
''Remark'': The derivative of the binormal vector is perpendicular to both the binormal and the tangent, hence it has to be proportional to the principal normal vector. The negative sign is simply a matter of convention: it is a byproduct of the historical development of the subject.
Geometric relevance: The torsion measures the turnaround of the binormal vector. The larger the torsion is, the faster the binormal vector rotates around the axis given by the tangent vector (see graphical illustrations). In the animated figure the rotation of the binormal vector is clearly visible at the peaks of the torsion function.
Properties
* A plane curve with non-vanishing curvature has zero torsion at all points. Conversely, if the torsion of a regular curve with non-vanishing curvature is identically zero, then this curve belongs to a fixed plane. * The curvature and the torsion of a helix are constant. Conversely, any space curve whose curvature and torsion are both constant and non-zero is a helix. The torsion is positive for a right-handed helix and is negative for a left-handed one.Alternative description
Let be the parametric equation of a space curve. Assume that this is a regular parametrization and that thecurvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
of the curve does not vanish. Analytically, is a three times differentiable function of with values in and the vectors
:
are linearly independent.
Then the torsion can be computed from the following formula:
:
Here the primes denote the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
s with respect to and the cross denotes the cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
. For , the formula in components is
:
Notes
References
* {{curvature Differential geometry Curves Curvature (mathematics) ru:Дифференциальная геометрия кривых#Кручение