strongly normalizing on:
[Wikipedia]
[Google]
[Amazon]
In
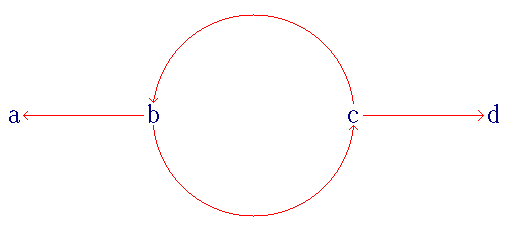 The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
abstract rewriting
In mathematical logic and theoretical computer science, an abstract rewriting system (also (abstract) reduction system or abstract rewrite system; abbreviated ARS) is a formalism that captures the quintessential notion and properties of rewriting s ...
, an object is in normal form if it cannot be rewritten any further, i.e. it is irreducible. Depending on the rewriting system, an object may rewrite to several normal forms or none at all. Many properties of rewriting systems relate to normal forms.
Definitions
Stated formally, if (''A'',→) is anabstract rewriting system
In mathematical logic and theoretical computer science, an abstract rewriting system (also (abstract) reduction system or abstract rewrite system; abbreviated ARS) is a formalism that captures the quintessential notion and properties of rewriting s ...
, ''x''∈''A'' is in normal form if no ''y''∈''A'' exists such that ''x''→''y'', i.e. ''x'' is an irreducible term.
An object ''a'' is weakly normalizing if there exists at least one particular sequence of rewrites starting from ''a'' that eventually yields a normal form. A rewriting system has the weak normalization property or is ''(weakly) normalizing'' (WN) if every object is weakly normalizing. An object ''a'' is strongly normalizing if every sequence of rewrites starting from ''a'' eventually terminates with a normal form. An abstract rewriting system is ''strongly normalizing'', ''terminating'', ''noetherian'', or has the (strong) normalization property (SN), if each of its objects is strongly normalizing.
A rewriting system has the ''normal form property'' (NF) if for all objects ''a'' and normal forms ''b'', ''b'' can be reached from ''a'' by a series of rewrites and inverse rewrites only if ''a'' reduces to ''b''. A rewriting system has the ''unique normal form property'' (UN) if for all normal forms ''a'', ''b'' ∈ ''S'', ''a'' can be reached from ''b'' by a series of rewrites and inverse rewrites only if ''a'' is equal to ''b''. A rewriting system has the ''unique normal form property with respect to reduction'' (UN→) if for every term reducing to normal forms ''a'' and ''b'', ''a'' is equal to ''b''.
Results
This section presents some well known results. First, SN implies WN.Confluence
In geography, a confluence (also: ''conflux'') occurs where two or more flowing bodies of water join to form a single channel. A confluence can occur in several configurations: at the point where a tributary joins a larger river (main stem); o ...
(abbreviated CR) implies NF implies UN implies UN→. The reverse implications do not generally hold. is UN→ but not UN as b=e and b,e are normal forms. is UN but not NF as b=c, c is a normal form, and b does not reduce to c. is NF as there are no normal forms, but not CR as a reduces to b and c, and b,c have no common reduct.
WN and UN→ imply confluence. Hence CR, NF, UN, and UN→ coincide if WN holds.
Examples
One example is that simplifying arithmetic expressions produces a number - in arithmetic, all numbers are normal forms. A remarkable fact is that all arithmetic expressions have a unique value, so the rewriting system is strongly normalizing and confluent: :(3 + 5) * (1 + 2) ⇒ 8 * (1 + 2) ⇒ 8 * 3 ⇒ 24 :(3 + 5) * (1 + 2) ⇒ (3 + 5) * 3 ⇒ 3*3 + 5*3 ⇒ 9 + 5*3 ⇒ 9 + 15 ⇒ 24 Examples of non-normalizing systems (not weakly or strongly) include counting to infinity (1 ⇒ 2 ⇒ 3 ⇒ ...) and loops such as the transformation function of theCollatz conjecture
The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integ ...
(1 ⇒ 2 ⇒ 4 ⇒ 1 ⇒ ..., it is an open problem if there are any other loops of the Collatz transformation). Another example is the single-rule system , which has no normalizing properties since from any term, e.g. ''r''(4,2) a single rewrite sequence starts, viz. ''r''(4,2) → ''r''(2,4) → ''r''(4,2) → ''r''(2,4) → ..., which is infinitely long. This leads to the idea of rewriting "modulo commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name ...
" where a term is in normal form if no rules but commutativity apply.
 The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
Untyped lambda calculus
The pure untyped lambda calculus does not satisfy the strong normalization property, and not even the weak normalization property. Consider the term (application is left associative). It has the following rewrite rule: For any term , : But consider what happens when we apply to itself: : Therefore the term is not strongly normalizing. And this is the only reduction sequence, hence it is not weakly normalizing either.Typed lambda calculus
Various systems of typed lambda calculus including the simply typed lambda calculus, Jean-Yves Girard's System F, andThierry Coquand
Thierry Coquand (; born 18 April 1961 in Jallieu, Isère, France) is a professor in computer science at the University of Gothenburg, known for his work in constructive mathematics, especially the calculus of constructions. He received his Ph.D. u ...
's calculus of constructions
In mathematical logic and computer science, the calculus of constructions (CoC) is a type theory created by Thierry Coquand. It can serve as both a typed programming language and as constructive foundation for mathematics. For this second reason ...
are strongly normalizing.
A lambda calculus system with the normalization property can be viewed as a programming language with the property that every program terminates. Although this is a very useful property, it has a drawback: a programming language with the normalization property cannot be Turing complete
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher, and theoretical biologist. Turing was highly influential in the development of theoretical com ...
, otherwise one could solve the halting problem by seeing if the program type-checks. That means that there are computable functions that cannot be defined in the simply typed lambda calculus (and similarly there are computable functions that cannot be computed in the calculus of constructions
In mathematical logic and computer science, the calculus of constructions (CoC) is a type theory created by Thierry Coquand. It can serve as both a typed programming language and as constructive foundation for mathematics. For this second reason ...
or System F), for example a self-interpreter.
See also
*Canonical form
In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides the simplest representation of an obj ...
* Typed lambda calculus
* Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or redu ...
* Total functional programming
* Barendregt–Geuvers–Klop conjecture __NOTOC__
In the branches of mathematical logic known as proof theory and type theory, a pure type system (PTS), previously known as a generalized type system (GTS), is a form of typed lambda calculus that allows an arbitrary number of sorts and d ...
* Newman's lemma In mathematics, in the theory of rewriting systems, Newman's lemma, also commonly called the diamond lemma, states that a terminating (or strongly normalizing) abstract rewriting system (ARS), that is, one in which there are no infinite reduction ...
* Normalization by evaluation
Notes
References
{{DEFAULTSORT:Normal Form (Term Rewriting) Computability theory Formal languages Rewriting systems Lambda calculus Logic in computer science