series expansion

In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division).

The resulting so-called '' series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non- analytic functions.

Types of series expansions

There are several kinds of series expansions, listed below.

A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function $f: U\to\mathbb$ is infinitely differentiable around a point $x_0$, then the Taylor series of ''f'' around this point is given by $\sum_^\frac(x - x_0)^n$ under the convention $0^0 := 1$. The ''Maclaurin series'' of a ''f'' is its Taylor series about $x_0 = 0$. A ''Laurent series'' is a generalization of the Taylor series, allowing negative exponent values; it takes the form $\sum_^ c_k (z - a)^k$ and converges in an annulus.

A ''general Dirichlet series'' is a series of the form $\sum_^ a_ne^$. One important special case of this is the ''ordinary Dirichlet series'' $\sum_^\frac$. Used in number theory.

A ''Fourier series'' is an expansion of periodic functions as a sum of many sine and cosine functions. More specifically, the Fourier series of a function $f(t)$ of period $2L$ is given by the expression $a_0 + \sum_^ (a_n\cos(\frac) + b_n\sin(\frac))$ where the coefficients are given by the formulae

$a_n := \frac\int_^L f(t)\cos(\frac)dt$$b_n := \frac\int_^L f(t)\sin(\frac)dt.$ In acoustics, e.g., the fundamental tone and the overtones together form an example of a Fourier series.

Newtonian series

Legendre polynomials: Used in physics to describe an arbitrary electrical field as a superposition of a dipole field, a quadrupole field, an octupole field, etc.

Zernike polynomials: Used in optics to calculate aberrations of optical systems. Each term in the series describes a particular type of aberration.

The '' Stirling series'' $\text\Gamma\left(z\right)\sim\left(z-\tfrac\right)\ln z-z+\tfrac\ln\left(2\pi\right)+\sum_^\frac$ is an approximation of the log-gamma function.

Examples

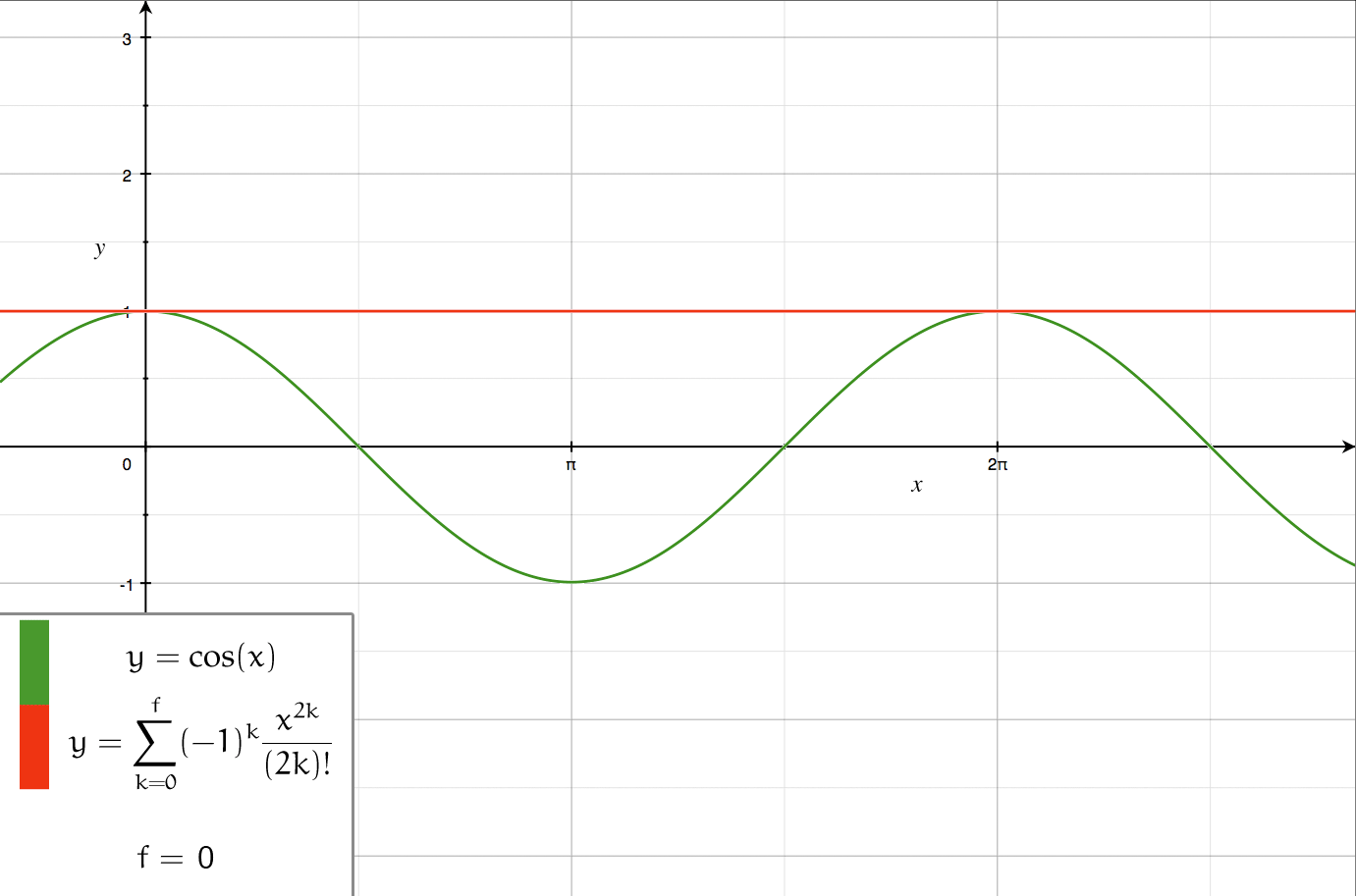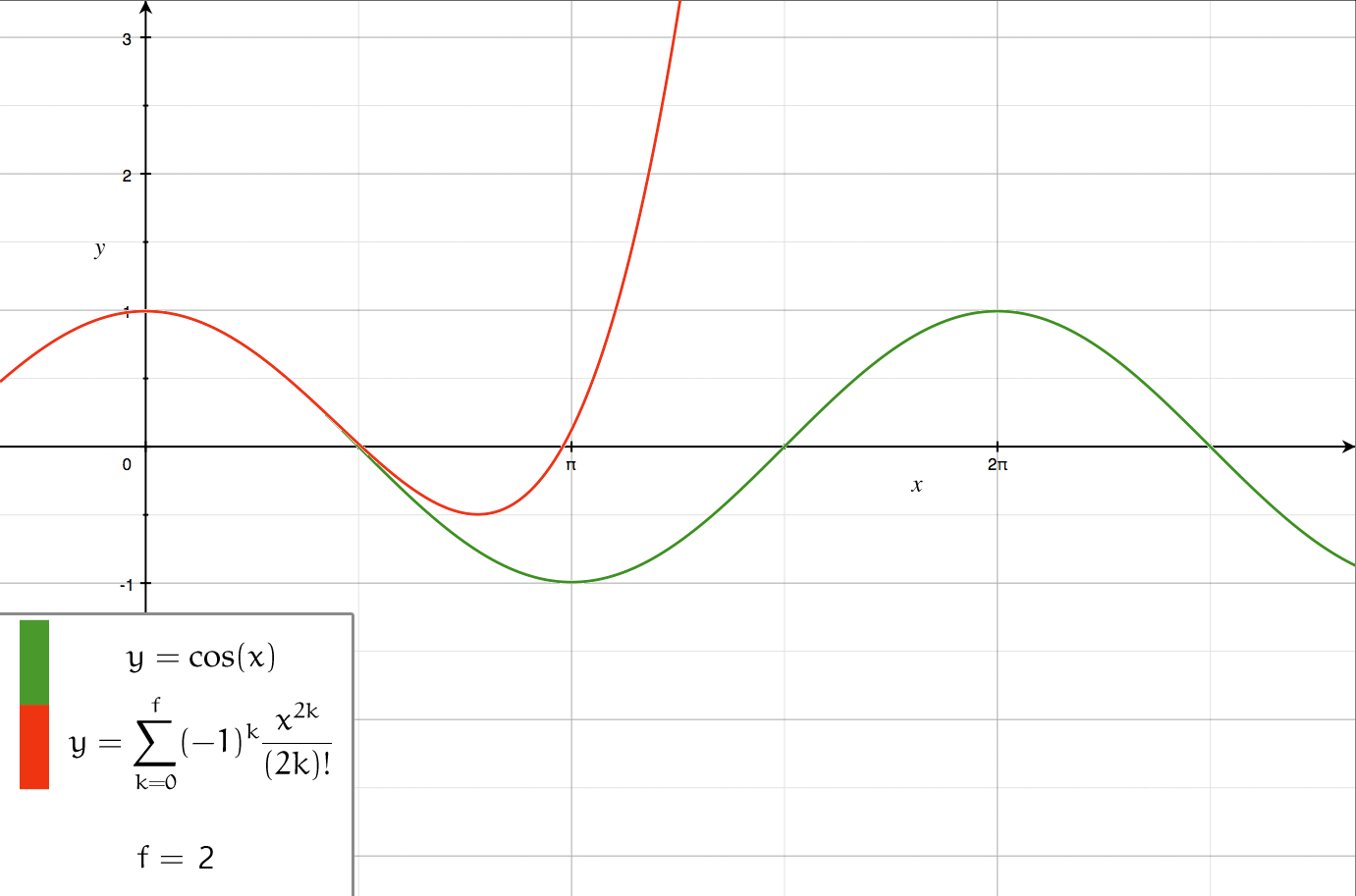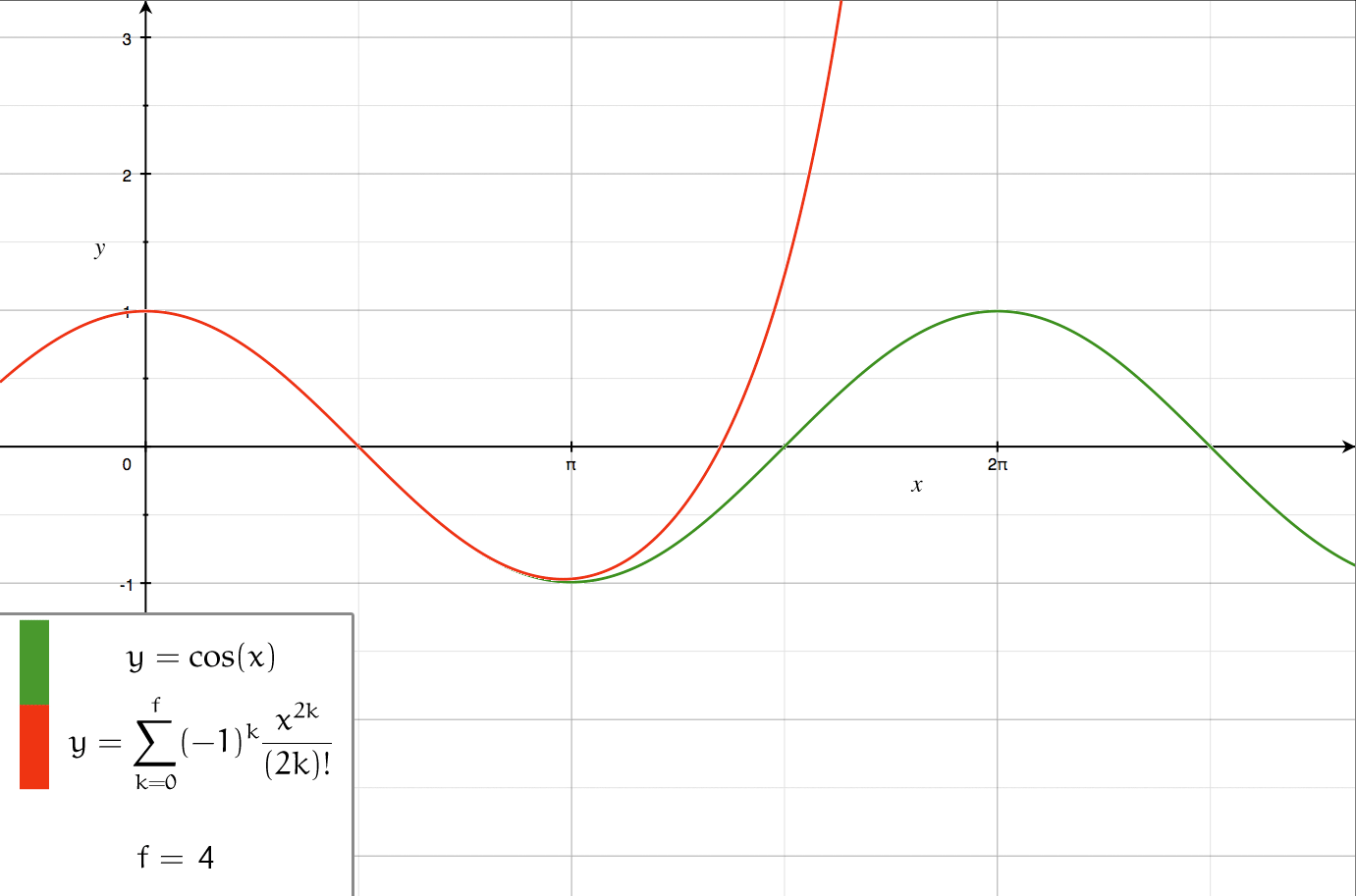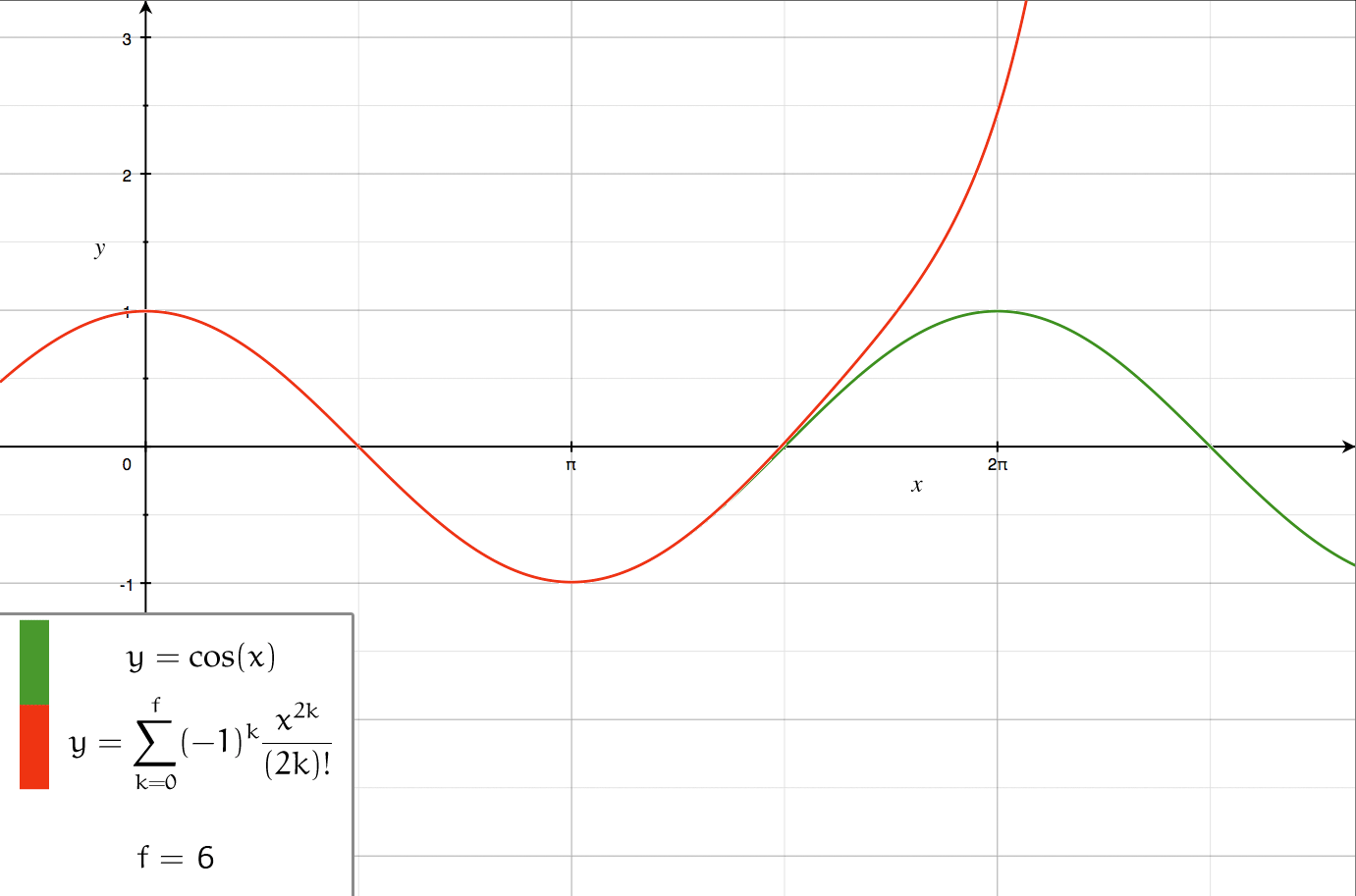
The following is the Taylor series of $e^x$:

$e^x=\sum^_\frac= 1 + x + \frac + \frac...$

The Dirichlet series of the Riemann zeta function is

$\zeta(s) := \sum_^ \frac = \frac + \frac{2^s} + \cdots$

References

Algebra
Polynomials
Mathematical analysis
Mathematical series