The second law of thermodynamics is a
physical law
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. The term ''law'' has diverse usage in many cases (approximate, accurate, broad, or narrow) ...
based on
universal empirical
Empirical evidence is evidence obtained through sense experience or experimental procedure. It is of central importance to the sciences and plays a role in various other fields, like epistemology and law.
There is no general agreement on how t ...
observation
Observation in the natural sciences is an act or instance of noticing or perceiving and the acquisition of information from a primary source. In living beings, observation employs the senses. In science, observation can also involve the percep ...
concerning
heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, ato ...
and
energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter (or 'downhill' in terms of the temperature gradient). Another statement is: "Not all heat can be converted into
work
Work may refer to:
* Work (human activity), intentional activity people perform to support themselves, others, or the community
** Manual labour, physical work done by humans
** House work, housework, or homemaking
** Working animal, an ani ...
in a
cyclic process."
[Young, H. D; Freedman, R. A. (2004). '' University Physics'', 11th edition. Pearson. p. 764.]
The second law of thermodynamics establishes the concept of
entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
as a physical property of a
thermodynamic system
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics.
Thermodynamic systems can be passive and active according to internal processes. According to inter ...
. It predicts whether processes are forbidden despite obeying the requirement of
conservation of energy
The law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be Conservation law, ''conserved'' over time. In the case of a Closed system#In thermodynamics, closed system, the principle s ...
as expressed in the
first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
and provides necessary criteria for
spontaneous process
In thermodynamics, a spontaneous process is a process which occurs without any external input to the system. A more technical definition is the time-evolution of a system in which it releases free energy and it moves to a lower, more thermodynamic ...
es. For example, the first law allows the process of a cup falling off a table and breaking on the floor, as well as allowing the reverse process of the cup fragments coming back together and 'jumping' back onto the table, while the second law allows the former and denies the latter. The second law may be formulated by the observation that the entropy of
isolated system
In physical science, an isolated system is either of the following:
# a physical system so far removed from other systems that it does not interact with them.
# a thermodynamic system enclosed by rigid immovable walls through which neither ...
s left to spontaneous evolution cannot decrease, as they always tend toward a state of
thermodynamic equilibrium
Thermodynamic equilibrium is a notion of thermodynamics with axiomatic status referring to an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable ...
where the entropy is highest at the given internal energy. An increase in the combined entropy of system and surroundings accounts for the
irreversibility
In thermodynamics, an irreversible process is a process that cannot be undone. All complex natural processes are irreversible, although a phase transition at the coexistence temperature (e.g. melting of ice cubes in water) is well approximated a ...
of natural processes, often referred to in the concept of the
arrow of time
An arrow is a fin-stabilized projectile launched by a bow. A typical arrow usually consists of a long, stiff, straight shaft with a weighty (and usually sharp and pointed) arrowhead attached to the front end, multiple fin-like stabilizers ca ...
.
Historically, the second law was an
empirical finding that was accepted as an
axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or ...
of
thermodynamic theory.
Statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
provides a microscopic explanation of the law in terms of
probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
s of the states of large assemblies of
atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
s or
molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemi ...
s. The second law has been expressed in many ways. Its first formulation, which preceded the proper definition of entropy and was based on
caloric theory
The caloric theory is an obsolete scientific theory that heat consists of a self-repellent fluid called caloric that flows from hotter bodies to colder bodies. Caloric was also thought of as a weightless gas that could pass in and out of pores ...
, is
Carnot's theorem, formulated by the French scientist
Sadi Carnot, who in 1824 showed that the efficiency of conversion of heat to work in a heat engine has an upper limit. The first rigorous definition of the second law based on the concept of entropy came from German scientist
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle ...
in the 1850s and included his statement that heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.
The second law of thermodynamics allows the definition of the concept of
thermodynamic temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion.
Thermodynamic temperature is typically expres ...
, but this has been formally delegated to the
zeroth law of thermodynamics
The zeroth law of thermodynamics is one of the four principal laws of thermodynamics. It provides an independent definition of temperature without reference to entropy, which is defined in the second law. The law was established by Ralph H. Fowl ...
.
Introduction
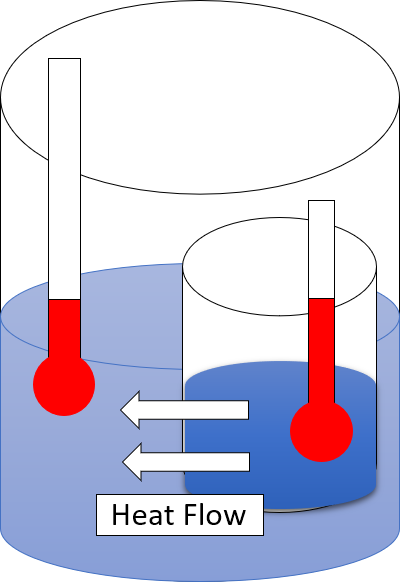
The
first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
provides the definition of the
internal energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accoun ...
of a
thermodynamic system
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics.
Thermodynamic systems can be passive and active according to internal processes. According to inter ...
, and expresses its change for a
closed system
A closed system is a natural physical system that does not allow transfer of matter in or out of the system, althoughin the contexts of physics, chemistry, engineering, etc.the transfer of energy (e.g. as work or heat) is allowed.
Physics
In cl ...
in terms of
work
Work may refer to:
* Work (human activity), intentional activity people perform to support themselves, others, or the community
** Manual labour, physical work done by humans
** House work, housework, or homemaking
** Working animal, an ani ...
and
heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, ato ...
. It can be linked to the law of
conservation of energy
The law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be Conservation law, ''conserved'' over time. In the case of a Closed system#In thermodynamics, closed system, the principle s ...
. Conceptually, the first law describes the fundamental principle that systems do not consume or 'use up' energy, that energy is neither created nor destroyed, but is simply converted from one form to another.
The second law is concerned with the direction of natural processes. It asserts that a natural process runs only in one sense, and is not reversible. That is, the state of a natural system itself can be reversed, but not without increasing the entropy of the system's surroundings, that is, both the state of the system plus the state of its surroundings cannot be together, fully reversed, without implying the destruction of entropy.
For example, when a path for conduction or
radiation
In physics, radiation is the emission or transmission of energy in the form of waves or particles through space or a material medium. This includes:
* ''electromagnetic radiation'' consisting of photons, such as radio waves, microwaves, infr ...
is made available, heat always flows spontaneously from a hotter to a colder body. Such
phenomena
A phenomenon ( phenomena), sometimes spelled phaenomenon, is an observable Event (philosophy), event. The term came into its modern Philosophy, philosophical usage through Immanuel Kant, who contrasted it with the noumenon, which ''cannot'' be ...
are accounted for in terms of
entropy change. A heat pump can reverse this heat flow, but the reversal process and the original process, both cause entropy production, thereby increasing the entropy of the system's surroundings. If an isolated system containing distinct subsystems is held initially in internal thermodynamic equilibrium by internal partitioning by impermeable walls between the subsystems, and then some operation makes the walls more permeable, then the system spontaneously evolves to reach a final new internal
thermodynamic equilibrium
Thermodynamic equilibrium is a notion of thermodynamics with axiomatic status referring to an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable ...
, and its total entropy,
, increases.
In a
reversible or
quasi-static, idealized process of transfer of energy as heat to a
closed thermodynamic system of interest, (which allows the entry or exit of energy – but not transfer of matter), from an auxiliary thermodynamic system, an infinitesimal increment (
) in the entropy of the system of interest is defined to result from an infinitesimal
transfer of heat (
) to the system of interest, divided by the common
thermodynamic temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion.
Thermodynamic temperature is typically expres ...
of the system of interest and the auxiliary thermodynamic system:
:
Different notations are used for an
infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " ...
amount of heat
and infinitesimal change of entropy
because entropy is a
function of state, while heat, like work, is not.
For an actually possible infinitesimal process without exchange of mass with the surroundings, the second law requires that the increment in system entropy fulfills the
inequality
:
This is because a general process for this case (no mass exchange between the system and its surroundings) may include work being done on the system by its surroundings, which can have frictional or viscous effects inside the system, because a chemical reaction may be in progress, or because heat transfer actually occurs only irreversibly, driven by a finite difference between the system temperature () and the temperature of the surroundings ().
[Adkins, C.J. (1968/1983), p. 75.]
The equality still applies for pure heat flow (only heat flow, no change in chemical composition and mass),
:
which is the basis of the accurate determination of the absolute entropy of pure substances from measured heat capacity curves and entropy changes at phase transitions, i.e. by calorimetry.
[Oxtoby, D. W; Gillis, H.P., Butler, L. J. (2015).''Principles of Modern Chemistry'', Brooks Cole. p. 617. ]
The
zeroth law of thermodynamics
The zeroth law of thermodynamics is one of the four principal laws of thermodynamics. It provides an independent definition of temperature without reference to entropy, which is defined in the second law. The law was established by Ralph H. Fowl ...
in its usual short statement allows recognition that two bodies in a relation of thermal equilibrium have the same temperature, especially that a test body has the same temperature as a reference thermometric body.
For a body in thermal equilibrium with another, there are indefinitely many empirical temperature scales, in general respectively depending on the properties of a particular reference thermometric body. The second law allows a distinguished temperature scale, which defines an absolute,
thermodynamic temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion.
Thermodynamic temperature is typically expres ...
, independent of the properties of any particular reference thermometric body.
Various statements of the law
The second law of thermodynamics may be expressed in many specific ways,
the most prominent classical statements being the statement by
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle ...
(1854), the statement by
Lord Kelvin
William Thomson, 1st Baron Kelvin (26 June 182417 December 1907), was a British mathematician, Mathematical physics, mathematical physicist and engineer. Born in Belfast, he was the Professor of Natural Philosophy (Glasgow), professor of Natur ...
(1851), and the statement in
axiomatic thermodynamics by
Constantin Carathéodory
Constantin Carathéodory (; 13 September 1873 – 2 February 1950) was a Greeks, Greek mathematician who spent most of his professional career in Germany. He made significant contributions to real and complex analysis, the calculus of variations, ...
(1909). These statements cast the law in general physical terms citing the impossibility of certain processes. The Clausius and the Kelvin statements have been shown to be equivalent.
Carnot's principle
The historical origin of the second law of thermodynamics was in
Sadi Carnot's theoretical analysis of the flow of heat in steam engines (1824). The centerpiece of that analysis, now known as a
Carnot engine, is an ideal
heat engine
A heat engine is a system that transfers thermal energy to do mechanical or electrical work. While originally conceived in the context of mechanical energy, the concept of the heat engine has been applied to various other kinds of energy, pa ...
fictively operated in the limiting mode of extreme slowness known as quasi-static, so that the heat and work transfers are between subsystems that are always in their own internal states of
thermodynamic equilibrium
Thermodynamic equilibrium is a notion of thermodynamics with axiomatic status referring to an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable ...
. It represents the theoretical maximum efficiency of a heat engine operating between any two given thermal or heat reservoirs at different temperatures. Carnot's principle was recognized by Carnot at a time when the
caloric theory
The caloric theory is an obsolete scientific theory that heat consists of a self-repellent fluid called caloric that flows from hotter bodies to colder bodies. Caloric was also thought of as a weightless gas that could pass in and out of pores ...
represented the dominant understanding of the nature of heat, before the recognition of the
first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
, and before the mathematical expression of the concept of entropy. Interpreted in the light of the first law, Carnot's analysis is physically equivalent to the second law of thermodynamics, and remains valid today. Some samples from his book are:
:: ...''wherever there exists a difference of temperature, motive power can be produced.''
:: The production of motive power is then due in
steam engines
A steam engine is a heat engine that performs Work (physics), mechanical work using steam as its working fluid. The steam engine uses the force produced by steam pressure to push a piston back and forth inside a Cylinder (locomotive), cyl ...
not to an actual consumption of caloric, but ''to its transportation from a warm body to a cold body ...''
:: ''The motive power of heat is independent of the agents employed to realize it; its quantity is fixed solely by the temperatures of the bodies between which is effected, finally, the transfer of caloric.''
In modern terms, Carnot's principle may be stated more precisely:
: The efficiency of a quasi-static or reversible
Carnot cycle
A Carnot cycle is an ideal thermodynamic cycle proposed by French physicist Nicolas Léonard Sadi Carnot, Sadi Carnot in 1824 and expanded upon by others in the 1830s and 1840s. By Carnot's theorem (thermodynamics), Carnot's theorem, it provides ...
depends only on the temperatures of the two heat reservoirs, and is the same, whatever the working substance. A Carnot engine operated in this way is the most efficient possible heat engine using those two temperatures.
Clausius statement
The German scientist
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle ...
laid the foundation for the second law of thermodynamics in 1850 by examining the relation between heat transfer and work. His formulation of the second law, which was published in German in 1854, is known as the ''Clausius statement'':
Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.
The statement by Clausius uses the concept of 'passage of heat'. As is usual in thermodynamic discussions, this means 'net transfer of energy as heat', and does not refer to contributory transfers one way and the other.
Heat cannot spontaneously flow from cold regions to hot regions without external work being performed on the system, which is evident from ordinary experience of
refrigeration
Refrigeration is any of various types of cooling of a space, substance, or system to lower and/or maintain its temperature below the ambient one (while the removed heat is ejected to a place of higher temperature).IIR International Dictionary of ...
, for example. In a refrigerator, heat is transferred from cold to hot, but only when forced by an external agent, the refrigeration system.
Kelvin statements
Lord Kelvin
William Thomson, 1st Baron Kelvin (26 June 182417 December 1907), was a British mathematician, Mathematical physics, mathematical physicist and engineer. Born in Belfast, he was the Professor of Natural Philosophy (Glasgow), professor of Natur ...
expressed the second law in several wordings.
:: It is impossible for a self-acting machine, unaided by any external agency, to convey heat from one body to another at a higher temperature.
:: It is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects.
Equivalence of the Clausius and the Kelvin statements
Suppose there is an engine violating the Kelvin statement: i.e., one that drains heat and converts it completely into work (the drained heat is fully converted to work) in a cyclic fashion without any other result. Now pair it with a reversed
Carnot engine as shown by the right figure. The
efficiency
Efficiency is the often measurable ability to avoid making mistakes or wasting materials, energy, efforts, money, and time while performing a task. In a more general sense, it is the ability to do things well, successfully, and without waste.
...
of a normal heat engine is ''η'' and so the efficiency of the reversed heat engine is 1/''η''. The net and sole effect of the combined pair of engines is to transfer heat
from the cooler reservoir to the hotter one, which violates the Clausius statement. This is a consequence of the
first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
, as for the total system's energy to remain the same;
, so therefore
, where (1) the sign convention of heat is used in which heat entering into (leaving from) an engine is positive (negative) and (2)
is obtained by
the definition of efficiency of the engine when the engine operation is not reversed. Thus a violation of the Kelvin statement implies a violation of the Clausius statement, i.e. the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, and hence the two are equivalent.
Planck's proposition
Planck offered the following proposition as derived directly from experience. This is sometimes regarded as his statement of the second law, but he regarded it as a starting point for the derivation of the second law.
:: It is impossible to construct an engine which will work in a complete cycle, and produce no effect except the production of work and cooling of a heat reservoir.
Relation between Kelvin's statement and Planck's proposition
It is almost customary in textbooks to speak of the "Kelvin–Planck statement" of the law, as for example in the text by
ter Haar and
Wergeland. This version, also known as the heat engine statement, of the second law states that
:: It is impossible to devise a
cyclically operating device, the sole effect of which is to absorb energy in the form of heat from a single
thermal reservoir and to deliver an equivalent amount of
work
Work may refer to:
* Work (human activity), intentional activity people perform to support themselves, others, or the community
** Manual labour, physical work done by humans
** House work, housework, or homemaking
** Working animal, an ani ...
.
Planck's statement
Max Planck
Max Karl Ernst Ludwig Planck (; ; 23 April 1858 – 4 October 1947) was a German Theoretical physics, theoretical physicist whose discovery of energy quantum, quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial con ...
stated the second law as follows.
:: Every process occurring in nature proceeds in the sense in which the sum of the entropies of all bodies taking part in the process is increased. In the limit, i.e. for reversible processes, the sum of the entropies remains unchanged.
[ Planck, M. (1897/1903), p. 100.][ Planck, M. (1926), p. 463, translation by Uffink, J. (2003), p. 131.][Roberts, J.K., Miller, A.R. (1928/1960), p. 382. This source is partly verbatim from Planck's statement, but does not cite Planck. This source calls the statement the principle of the increase of entropy.]
Rather like Planck's statement is that of
George Uhlenbeck
George Eugene Uhlenbeck (December 6, 1900 – October 31, 1988) was a Dutch-American theoretical physicist, known for his significant contributions to quantum mechanics and statistical mechanics. He co-developed the concept of electron spin, alo ...
and G. W. Ford for ''irreversible phenomena''.
:: ... in an irreversible or spontaneous change from one equilibrium state to another (as for example the equalization of temperature of two bodies A and B, when brought in contact) the entropy always increases.
Principle of Carathéodory
Constantin Carathéodory
Constantin Carathéodory (; 13 September 1873 – 2 February 1950) was a Greeks, Greek mathematician who spent most of his professional career in Germany. He made significant contributions to real and complex analysis, the calculus of variations, ...
formulated thermodynamics on a purely mathematical axiomatic foundation. His statement of the second law is known as the Principle of Carathéodory, which may be formulated as follows:
In every neighborhood of any state S of an adiabatically enclosed system there are states inaccessible from S.
With this formulation, he described the concept of
adiabatic accessibility for the first time and provided the foundation for a new subfield of classical thermodynamics, often called
geometrical thermodynamics. It follows from Carathéodory's principle that quantity of energy quasi-statically transferred as heat is a holonomic
process function
In thermodynamics, a quantity that is well defined so as to describe the path of a process through the equilibrium state space of a thermodynamic system is termed a process function, or, alternatively, a process quantity, or a path function. A ...
, in other words,
.
Though it is almost customary in textbooks to say that Carathéodory's principle expresses the second law and to treat it as equivalent to the Clausius or to the Kelvin-Planck statements, such is not the case. To get all the content of the second law, Carathéodory's principle needs to be supplemented by Planck's principle, that isochoric work always increases the internal energy of a closed system that was initially in its own internal thermodynamic equilibrium.
[Münster, A. (1970), p. 45.][ Planck, M. (1926).]
Planck's principle
In 1926, Max Planck wrote an important paper on the basics of thermodynamics.
He indicated the principle
:: The internal energy of a closed system is increased by an adiabatic process, throughout the duration of which, the volume of the system remains constant.
This formulation does not mention heat and does not mention temperature, nor even entropy, and does not necessarily implicitly rely on those concepts, but it implies the content of the second law. A closely related statement is that "Frictional pressure never does positive work." Planck wrote: "The production of heat by friction is irreversible."
Not mentioning entropy, this principle of Planck is stated in physical terms. It is very closely related to the Kelvin statement given just above. It is relevant that for a system at constant volume and
mole numbers, the entropy is a monotonic function of the internal energy. Nevertheless, this principle of Planck is not actually Planck's preferred statement of the second law, which is quoted above, in a previous sub-section of the present section of this present article, and relies on the concept of entropy.
A statement that in a sense is complementary to Planck's principle is made by Claus Borgnakke and Richard E. Sonntag. They do not offer it as a full statement of the second law:
:: ... there is only one way in which the entropy of a
losedsystem can be decreased, and that is to transfer heat from the system.
Differing from Planck's just foregoing principle, this one is explicitly in terms of entropy change. Removal of matter from a system can also decrease its entropy.
Relating the second law to the definition of temperature
The second law has been shown to be equivalent to the
internal energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accoun ...
defined as a
convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
of the other extensive properties of the system. That is, when a system is described by stating its
internal energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accoun ...
, an extensive variable, as a function of its
entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
, volume , and mol number , i.e. ), then the temperature is equal to the
partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
of the internal energy with respect to the entropy
[ Callen, H.B. (1960/1985), ''Thermodynamics and an Introduction to Thermostatistics'', (first edition 1960), second edition 1985, John Wiley & Sons, New York, , pp. 146–148.] (essentially equivalent to the first equation for and held constant):
:
Second law statements, such as the Clausius inequality, involving radiative fluxes
The Clausius inequality, as well as some other statements of the second law, must be re-stated to have general applicability for all forms of heat transfer, i.e. scenarios involving radiative fluxes. For example, the integrand (đQ/T) of the Clausius expression applies to heat conduction and convection, and the case of ideal infinitesimal blackbody radiation (BR) transfer, but does not apply to most radiative transfer scenarios and in some cases has no physical meaning whatsoever. Consequently, the Clausius inequality was re-stated so that it is applicable to cycles with processes involving any form of heat transfer. The entropy transfer with radiative fluxes (
) is taken separately from that due to heat transfer by conduction and convection (
), where the temperature is evaluated at the system boundary where the heat transfer occurs. The modified Clausius inequality, for all heat transfer scenarios, can then be expressed as,
In a nutshell, the Clausius inequality is saying that when a cycle is completed, the change in the state property S will be zero, so the entropy that was produced during the cycle must have transferred out of the system by heat transfer. The
(or đ) indicates a path dependent integration.
Due to the inherent emission of radiation from all matter, most entropy flux calculations involve incident, reflected and emitted radiative fluxes. The energy and entropy of unpolarized blackbody thermal radiation, is calculated using the spectral energy and entropy radiance expressions derived by Max Planck using equilibrium statistical mechanics,
where ''c'' is the speed of light, ''k'' is the Boltzmann constant, ''h'' is the Planck constant, ''ν'' is frequency, and the quantities ''K''
v and ''L''
v are the energy and entropy fluxes per unit frequency, area, and solid angle. In deriving this blackbody spectral entropy radiance, with the goal of deriving the blackbody energy formula, Planck postulated that the energy of a photon was quantized (partly to simplify the mathematics), thereby starting quantum theory.
A non-equilibrium statistical mechanics approach has also been used to obtain the same result as Planck, indicating it has wider significance and represents a non-equilibrium entropy. A plot of ''K''
v versus frequency (v) for various values of temperature (''T)'' gives a family of blackbody radiation energy spectra, and likewise for the entropy spectra. For non-blackbody radiation (NBR) emission fluxes, the spectral entropy radiance ''L''
v is found by substituting ''K''
v spectral energy radiance data into the ''L''
v expression (noting that emitted and reflected entropy fluxes are, in general, not independent). For the emission of NBR, including graybody radiation (GR), the resultant emitted entropy flux, or radiance ''L'', has a higher ratio of entropy-to-energy (''L/K''), than that of BR. That is, the entropy flux of NBR emission is farther removed from the conduction and convection ''q''/''T'' result, than that for BR emission. This observation is consistent with Max Planck's blackbody radiation energy and entropy formulas and is consistent with the fact that blackbody radiation emission represents the maximum emission of entropy for all materials with the same temperature, as well as the maximum entropy emission for all radiation with the same energy radiance.
Generalized conceptual statement of the second law principle
Second law analysis is valuable in scientific and engineering analysis in that it provides a number of benefits over energy analysis alone, including the basis for determining energy quality (exergy content), understanding fundamental physical phenomena, and improving performance evaluation and optimization. As a result, a conceptual statement of the principle is very useful in engineering analysis. Thermodynamic systems can be categorized by the four combinations of either entropy (S) up or down, and uniformity (Y) – between system and its environment – up or down. This 'special' category of processes, category IV, is characterized by movement in the direction of low disorder and low uniformity, counteracting the second law tendency towards uniformity and disorder.

The second law can be conceptually stated
as follows: Matter and energy have the tendency to reach a state of uniformity or internal and external equilibrium, a state of maximum disorder (entropy). Real non-equilibrium processes always produce entropy, causing increased disorder in the universe, while idealized reversible processes produce no entropy and no process is known to exist that destroys entropy. The tendency of a system to approach uniformity may be counteracted, and the system may become more ordered or complex, by the combination of two things, a work or exergy source and some form of instruction or intelligence. Where 'exergy' is the thermal, mechanical, electric or chemical work potential of an energy source or flow, and 'instruction or intelligence', although subjective, is in the context of the set of category IV processes.
Consider a category IV example of robotic manufacturing and assembly of vehicles in a factory. The robotic machinery requires electrical work input and instructions, but when completed, the manufactured products have less uniformity with their surroundings, or more complexity (higher order) relative to the raw materials they were made from. Thus, system entropy or disorder decreases while the tendency towards uniformity between the system and its environment is counteracted. In this example, the instructions, as well as the source of work may be internal or external to the system, and they may or may not cross the system boundary. To illustrate, the instructions may be pre-coded and the electrical work may be stored in an energy storage system on-site. Alternatively, the control of the machinery may be by remote operation over a communications network, while the electric work is supplied to the factory from the local electric grid. In addition, humans may directly play, in whole or in part, the role that the robotic machinery plays in manufacturing. In this case, instructions may be involved, but intelligence is either directly responsible, or indirectly responsible, for the direction or application of work in such a way as to counteract the tendency towards disorder and uniformity.
There are also situations where the entropy spontaneously decreases by means of energy and entropy transfer. When thermodynamic constraints are not present, spontaneously energy or mass, as well as accompanying entropy, may be transferred out of a system in a progress to reach external equilibrium or uniformity in intensive properties of the system with its surroundings. This occurs spontaneously because the energy or mass transferred from the system to its surroundings results in a higher entropy in the surroundings, that is, it results in higher overall entropy of the system plus its surroundings. Note that this transfer of entropy requires dis-equilibrium in properties, such as a temperature difference. One example of this is the cooling crystallization of water that can occur when the system's surroundings are below freezing temperatures. Unconstrained heat transfer can spontaneously occur, leading to water molecules freezing into a crystallized structure of reduced disorder (sticking together in a certain order due to molecular attraction). The entropy of the system decreases, but the system approaches uniformity with its surroundings (category III).
On the other hand, consider the refrigeration of water in a warm environment. Due to refrigeration, as heat is extracted from the water, the temperature and entropy of the water decreases, as the system moves further away from uniformity with its warm surroundings or environment (category IV). The main point, take-away, is that refrigeration not only requires a source of work, it requires designed equipment, as well as pre-coded or direct operational intelligence or instructions to achieve the desired refrigeration effect.
Corollaries
Perpetual motion of the second kind
Before the establishment of the second law, many people who were interested in inventing a perpetual motion machine had tried to circumvent the restrictions of
first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
by extracting the massive internal energy of the environment as the power of the machine. Such a machine is called a "perpetual motion machine of the second kind". The second law declared the impossibility of such machines.
Carnot's theorem
Carnot's theorem (1824) is a principle that limits the maximum efficiency for any possible engine. The efficiency solely depends on the temperature difference between the hot and cold thermal reservoirs. Carnot's theorem states:
* All irreversible heat engines between two heat reservoirs are less efficient than a
Carnot engine operating between the same reservoirs.
* All reversible heat engines between two heat reservoirs are equally efficient with a Carnot engine operating between the same reservoirs.
In his ideal model, the heat of caloric converted into work could be reinstated by reversing the motion of the cycle, a concept subsequently known as
thermodynamic reversibility. Carnot, however, further postulated that some caloric is lost, not being converted to mechanical work. Hence, no real heat engine could realize the
Carnot cycle
A Carnot cycle is an ideal thermodynamic cycle proposed by French physicist Nicolas Léonard Sadi Carnot, Sadi Carnot in 1824 and expanded upon by others in the 1830s and 1840s. By Carnot's theorem (thermodynamics), Carnot's theorem, it provides ...
's reversibility and was condemned to be less efficient.
Though formulated in terms of caloric (see the obsolete
caloric theory
The caloric theory is an obsolete scientific theory that heat consists of a self-repellent fluid called caloric that flows from hotter bodies to colder bodies. Caloric was also thought of as a weightless gas that could pass in and out of pores ...
), rather than
entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
, this was an early insight into the second law.
Clausius inequality
The
Clausius theorem (1854) states that in a cyclic process
:
The equality holds in the reversible case and the strict inequality holds in the irreversible case, with ''T''
surr as the temperature of the heat bath (surroundings) here. The reversible case is used to introduce the state function
entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
. This is because in cyclic processes the variation of a state function is zero from state functionality.
Thermodynamic temperature
For an arbitrary heat engine, the efficiency is:
where ''W''
''n'' is the net work done by the engine per cycle, ''q''
H > 0 is the heat added to the engine from a hot reservoir, and ''q''
C = − < 0
[.] is waste
heat given off to a cold reservoir from the engine. Thus the efficiency depends only on the ratio / .
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, any reversible heat engine operating between temperatures ''T''
H and ''T''
C must have the same efficiency, that is to say, the efficiency is a function of temperatures only:
In addition, a reversible heat engine operating between temperatures ''T''
1 and ''T''
3 must have the same efficiency as one consisting of two cycles, one between ''T''
1 and another (intermediate) temperature ''T''
2, and the second between ''T''
2 and ''T''
3, where ''T''
1 > ''T''
2 > ''T''
3. This is because, if a part of the two cycle engine is hidden such that it is recognized as an engine between the reservoirs at the temperatures ''T''
1 and ''T''
3, then the efficiency of this engine must be same to the other engine at the same reservoirs. If we choose engines such that work done by the one cycle engine and the two cycle engine are same, then the efficiency of each heat engine is written as the below.
:
,
:
,
:
.
Here, the engine 1 is the one cycle engine, and the engines 2 and 3 make the two cycle engine where there is the intermediate reservoir at ''T''
2. We also have used the fact that the heat
passes through the intermediate thermal reservoir at
without losing its energy. (I.e.,
is not lost during its passage through the reservoir at
.) This fact can be proved by the following.
:
In order to have the consistency in the last equation, the heat
flown from the engine 2 to the intermediate reservoir must be equal to the heat
flown out from the reservoir to the engine 3.
Then
:
Now consider the case where
is a fixed reference temperature: the temperature of the
triple point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three Phase (matter), phases (gas, liquid, and solid) of that substance coexist in thermodynamic equilibrium.. It is that temperature and pressure at ...
of water as 273.16 K;
. Then for any ''T''
2 and ''T''
3,
:
Therefore, if thermodynamic temperature ''T''* is defined by
:
then the function ''f'', viewed as a function of thermodynamic temperatures, is simply
:
and the reference temperature ''T''
1* = 273.16 K × ''f''(''T''
1,''T''
1) = 273.16 K. (Any reference temperature and any positive numerical value could be usedthe choice here corresponds to the
Kelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By de ...
scale.)
Entropy
According to the
Clausius equality, for a ''reversible process''
:
That means the line integral
is path independent for reversible processes.
So we can define a state function ''S'' called entropy, which for a reversible process or for pure heat transfer satisfies
:
With this we can only obtain the difference of entropy by integrating the above formula. To obtain the absolute value, we need the
third law of thermodynamics
The third law of thermodynamics states that the entropy of a closed system at thermodynamic equilibrium approaches a constant value when its temperature approaches absolute zero. This constant value cannot depend on any other parameters characte ...
, which states that ''S'' = 0 at
absolute zero
Absolute zero is the lowest possible temperature, a state at which a system's internal energy, and in ideal cases entropy, reach their minimum values. The absolute zero is defined as 0 K on the Kelvin scale, equivalent to −273.15 ° ...
for perfect crystals.
For any irreversible process, since entropy is a state function, we can always connect the initial and terminal states with an imaginary reversible process and integrating on that path to calculate the difference in entropy.
Now reverse the reversible process and combine it with the said irreversible process. Applying the
Clausius inequality on this loop, with ''T''
surr as the temperature of the surroundings,
:
Thus,
:
where the equality holds if the transformation is reversible. If the process is an
adiabatic process
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its Environment (systems), environment. Unlike an isothermal process, an adiabatic process transf ...
, then
, so
.
Energy, available useful work
An important and revealing idealized special case is to consider applying the second law to the scenario of an isolated system (called the total system or universe), made up of two parts: a sub-system of interest, and the sub-system's surroundings. These surroundings are imagined to be so large that they can be considered as an ''unlimited'' heat reservoir at temperature ''T''
R and pressure ''P''
R so that no matter how much heat is transferred to (or from) the sub-system, the temperature of the surroundings will remain ''T''
R; and no matter how much the volume of the sub-system expands (or contracts), the pressure of the surroundings will remain ''P''
R.
Whatever changes to ''dS'' and ''dS''
R occur in the entropies of the sub-system and the surroundings individually, the entropy ''S''
tot of the isolated total system must not decrease according to the second law of thermodynamics:
:
According to the
first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
, the change ''dU'' in the internal energy of the sub-system is the sum of the heat ''δq'' added to the sub-system, ''minus'' any work ''δw'' done ''by'' the sub-system, ''plus'' any net chemical energy entering the sub-system ''d'' Σ''μ
iRN
i'', so that:
:
where ''μ''
''iR'' are the
chemical potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potent ...
s of chemical species in the external surroundings.
Now the heat leaving the reservoir and entering the sub-system is
:
where we have first used the definition of entropy in classical thermodynamics (alternatively, in statistical thermodynamics, the relation between entropy change, temperature and absorbed heat can be derived); and then the second law inequality from above.
It therefore follows that any net work ''δw'' done by the sub-system must obey
:
It is useful to separate the work ''δw'' done by the subsystem into the ''useful'' work ''δw
u'' that can be done ''by'' the sub-system, over and beyond the work ''p
R dV'' done merely by the sub-system expanding against the surrounding external pressure, giving the following relation for the useful work (exergy) that can be done:
:
It is convenient to define the right-hand-side as the exact derivative of a thermodynamic potential, called the ''availability'' or ''
exergy
Exergy, often referred to as "available energy" or "useful work potential", is a fundamental concept in the field of thermodynamics and engineering. It plays a crucial role in understanding and quantifying the quality of energy within a system and ...
'' ''E'' of the subsystem,
:
The second law therefore implies that for any process which can be considered as divided simply into a subsystem, and an unlimited temperature and pressure reservoir with which it is in contact,
:
i.e. the change in the subsystem's exergy plus the useful work done ''by'' the subsystem (or, the change in the subsystem's exergy less any work, additional to that done by the pressure reservoir, done ''on'' the system) must be less than or equal to zero.
In sum, if a proper ''infinite-reservoir-like'' reference state is chosen as the system surroundings in the real world, then the second law predicts a decrease in ''E'' for an irreversible process and no change for a reversible process.
:
is equivalent to
This expression together with the associated reference state permits a
design engineer
A design engineer is an engineer focused on the engineering design process in any of the various engineering disciplines (including civil, mechanical, electrical, chemical, textiles, aerospace, nuclear, manufacturing, systems, and struct ...
working at the macroscopic scale (above the
thermodynamic limit
In statistical mechanics, the thermodynamic limit or macroscopic limit, of a system is the Limit (mathematics), limit for a large number of particles (e.g., atoms or molecules) where the volume is taken to grow in proportion with the number of ...
) to utilize the second law without directly measuring or considering entropy change in a total isolated system (see also ''
Process engineer''). Those changes have already been considered by the assumption that the system under consideration can reach equilibrium with the reference state without altering the reference state. An efficiency for a process or collection of processes that compares it to the reversible ideal may also be found (see ''
Exergy efficiency
In thermal engineering, exergy efficiency (also known as the second-law efficiency or rational efficiency) computes the effectiveness of a system relative to its performance in reversible conditions. It is defined as the ratio of the thermal effi ...
'').
This approach to the second law is widely utilized in
engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
practice,
environmental accounting
Environmental accounting is a subset of accounting proper, its target being to incorporate both economic and environmental information. It can be conducted at the corporate level or at the level of a national economy through the System of Integrat ...
,
systems ecology
Systems ecology is an interdisciplinary field of ecology, a subset of Earth system science, that takes a holistic approach to the study of ecological systems, especially ecosystems. Systems ecology can be seen as an application of general syste ...
, and other disciplines.
Direction of spontaneous processes
The second law determines whether a proposed physical or chemical process is forbidden or may occur spontaneously. For
isolated system
In physical science, an isolated system is either of the following:
# a physical system so far removed from other systems that it does not interact with them.
# a thermodynamic system enclosed by rigid immovable walls through which neither ...
s, no energy is provided by the surroundings and the second law requires that the entropy of the system alone cannot decrease: Δ''S'' ≥ 0. Examples of spontaneous physical processes in isolated systems include the following:
* 1)
Heat can be transferred from a region of higher temperature to a lower temperature (but not the reverse).
* 2) Mechanical energy can be converted to thermal energy (but not the reverse).
* 3) A solute can move from a region of higher concentration to a region of lower concentration (but not the reverse).
However, for some non-isolated systems which can exchange energy with their surroundings, the surroundings exchange enough heat with the system, or do sufficient work on the system, so that the processes occur in the opposite direction. In such a case, the reverse process can occur because it is ''coupled'' to a simultaneous process that ''increases'' the entropy of the surroundings. The coupled process will go forward provided that the total entropy change of the system and surroundings combined is nonnegative as required by the second law: Δ''S''
tot = Δ''S'' + Δ''S''
R ≥ 0. For the three examples given above:
* 1) Heat can be transferred from a region of lower temperature to a higher temperature by a
refrigerator
A refrigerator, commonly shortened to fridge, is a commercial and home appliance consisting of a thermal insulation, thermally insulated compartment and a heat pump (mechanical, electronic or chemical) that transfers heat from its inside to ...
or
heat pump
A heat pump is a device that uses electricity to transfer heat from a colder place to a warmer place. Specifically, the heat pump transfers thermal energy using a heat pump and refrigeration cycle, cooling the cool space and warming the warm s ...
, provided that the device delivers sufficient mechanical work to the system and converts it to thermal energy inside the system.
* 2) Thermal energy can be converted by a heat engine to mechanical work within a system at a single temperature, provided that the heat engine transfers a sufficient amount of heat from the system to a lower-temperature region in the surroundings.
* 3) A solute can travel from a region of lower concentration to a region of higher concentration in the biochemical process of
active transport
In cellular biology, active transport is the movement of molecules or ions across a cell membrane from a region of lower concentration to a region of higher concentration—against the concentration gradient. Active transport requires cellula ...
, if sufficient work is provided by a concentration gradient of a chemical such as
ATP or by an
electrochemical gradient
An electrochemical gradient is a gradient of electrochemical potential, usually for an ion that can move across a membrane. The gradient consists of two parts:
* The chemical gradient, or difference in Concentration, solute concentration across ...
.
Second law in chemical thermodynamics
For a
spontaneous chemical process in a closed system at constant temperature and pressure without non-''PV'' work, the Clausius inequality Δ''S'' > ''Q/T''
surr transforms into a condition for the change in
Gibbs free energy
In thermodynamics, the Gibbs free energy (or Gibbs energy as the recommended name; symbol is a thermodynamic potential that can be used to calculate the maximum amount of Work (thermodynamics), work, other than Work (thermodynamics)#Pressure–v ...
:
or d''G'' < 0. For a similar process at constant temperature and volume, the change in
Helmholtz free energy
In thermodynamics, the Helmholtz free energy (or Helmholtz energy) is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature ( isothermal). The change in the Helmholtz ene ...
must be negative,
. Thus, a negative value of the change in free energy (''G'' or ''A'') is a necessary condition for a process to be spontaneous. This is the most useful form of the second law of thermodynamics in chemistry, where free-energy changes can be calculated from tabulated enthalpies of formation and standard molar entropies of reactants and products.
The chemical equilibrium condition at constant ''T'' and ''p'' without electrical work is d''G'' = 0.
History

The first theory of the conversion of heat into mechanical work is due to
Nicolas Léonard Sadi Carnot
Nicolas Léonard Sadi Carnot (; 1 June 1796 – 24 August 1832) was a French people, French military engineering, military engineer and physicist. A graduate of the École polytechnique, Carnot served as an officer in the Engineering Arm (''le ...
in 1824. He was the first to realize correctly that the efficiency of this conversion depends on the difference of temperature between an engine and its surroundings.
Recognizing the significance of
James Prescott Joule's work on the conservation of energy,
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle ...
was the first to formulate the second law during 1850, in this form: heat does not flow ''spontaneously'' from cold to hot bodies. While common knowledge now, this was contrary to the
caloric theory
The caloric theory is an obsolete scientific theory that heat consists of a self-repellent fluid called caloric that flows from hotter bodies to colder bodies. Caloric was also thought of as a weightless gas that could pass in and out of pores ...
of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).
Established during the 19th century, the
Kelvin-Planck statement of the second law says, "It is impossible for any device that operates on a
cycle to receive heat from a single
reservoir
A reservoir (; ) is an enlarged lake behind a dam, usually built to water storage, store fresh water, often doubling for hydroelectric power generation.
Reservoirs are created by controlling a watercourse that drains an existing body of wa ...
and produce a net amount of work." This statement was shown to be equivalent to the statement of Clausius.
The
ergodic hypothesis is also important for the
Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over a long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.
There is a traditional doctrine, starting with Clausius, that entropy can be understood in terms of molecular 'disorder' within a
macroscopic system. This doctrine is obsolescent.
[Entropy Sites — A Guide]
Content selected by Frank L. Lambert
Account given by Clausius

In 1865, the German physicist
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle ...
stated what he called the "second fundamental theorem in the
mechanical theory of heat" in the following form:
:
where ''Q'' is heat, ''T'' is temperature and ''N'' is the "equivalence-value" of all uncompensated transformations involved in a cyclical process. Later, in 1865, Clausius would come to define "equivalence-value" as entropy. On the heels of this definition, that same year, the most famous version of the second law was read in a presentation at the Philosophical Society of Zurich on April 24, in which, in the end of his presentation, Clausius concludes:
The entropy of the universe tends to a maximum.
This statement is the best-known phrasing of the second law. Because of the looseness of its language, e.g.
universe
The universe is all of space and time and their contents. It comprises all of existence, any fundamental interaction, physical process and physical constant, and therefore all forms of matter and energy, and the structures they form, from s ...
, as well as lack of specific conditions, e.g. open, closed, or isolated, many people take this simple statement to mean that the second law of thermodynamics applies virtually to every subject imaginable. This is not true; this statement is only a simplified version of a more extended and precise description.
In terms of time variation, the mathematical statement of the second law for an
isolated system
In physical science, an isolated system is either of the following:
# a physical system so far removed from other systems that it does not interact with them.
# a thermodynamic system enclosed by rigid immovable walls through which neither ...
undergoing an arbitrary transformation is:
:
where
: ''S'' is the entropy of the system and
: ''t'' is
time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
.
The equality sign applies after equilibration. An alternative way of formulating of the second law for isolated systems is:
:
with
with
the sum of the rate of
entropy production
Entropy production (or generation) is the amount of entropy which is produced during heat process to evaluate the efficiency of the process.
Short history
Entropy is produced in irreversible processes. The importance of avoiding irreversible p ...
by all processes inside the system. The advantage of this formulation is that it shows the effect of the entropy production. The rate of entropy production is a very important concept since it determines (limits) the efficiency of thermal machines. Multiplied with ambient temperature
it gives the so-called dissipated energy
.
The expression of the second law for closed systems (so, allowing heat exchange and moving boundaries, but not exchange of matter) is:
:
with
Here,
:
is the heat flow into the system
:
is the temperature at the point where the heat enters the system.
The equality sign holds in the case that only reversible processes take place inside the system. If irreversible processes take place (which is the case in real systems in operation) the >-sign holds. If heat is supplied to the system at several places we have to take the algebraic sum of the corresponding terms.
For open systems (also allowing exchange of matter):
:
with
Here,
is the flow of entropy into the system associated with the flow of matter entering the system. It should not be confused with the time derivative of the entropy. If matter is supplied at several places we have to take the algebraic sum of these contributions.
Statistical mechanics
Statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
gives an explanation for the second law by postulating that a material is composed of atoms and molecules which are in constant motion. A particular set of positions and velocities for each particle in the system is called a
microstate
A microstate or ministate is a sovereign state having a very small population or land area, usually both. However, the meanings of "state" and "very small" are not well-defined in international law. Some recent attempts to define microstates ...
of the system and because of the constant motion, the system is constantly changing its microstate. Statistical mechanics postulates that, in equilibrium, each microstate that the system might be in is equally likely to occur, and when this assumption is made, it leads directly to the conclusion that the second law must hold in a statistical sense. That is, the second law will hold on average, with a statistical variation on the order of 1/ where ''N'' is the number of particles in the system. For everyday (macroscopic) situations, the probability that the second law will be violated is practically zero. However, for systems with a small number of particles, thermodynamic parameters, including the entropy, may show significant statistical deviations from that predicted by the second law. Classical thermodynamic theory does not deal with these statistical variations.
Derivation from statistical mechanics
The first mechanical argument of the
Kinetic theory of gases
The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. Its introduction allowed many principal concepts of thermodynamics to be established. It treats a gas as composed of numerous particles, too small ...
that molecular collisions entail an equalization of temperatures and hence a tendency towards equilibrium was due to
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
in 1860;
Ludwig Boltzmann
Ludwig Eduard Boltzmann ( ; ; 20 February 1844 – 5 September 1906) was an Austrian mathematician and Theoretical physics, theoretical physicist. His greatest achievements were the development of statistical mechanics and the statistical ex ...
with his
H-theorem
In classical statistical mechanics, the ''H''-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency of the quantity ''H'' (defined below) to decrease in a nearly-ideal gas of molecules.L. Boltzmann,Weitere Studien über das Wär ...
of 1872 also argued that due to collisions gases should over time tend toward the
Maxwell–Boltzmann distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.
It was first defined and use ...
.
Due to
Loschmidt's paradox
In physics, Loschmidt's paradox (named for Josef Loschmidt), also known as the reversibility paradox, irreversibility paradox, or ' (), is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics ...
, derivations of the second law have to make an assumption regarding the past, namely that the system is
uncorrelated
In probability theory and statistics, two real-valued random variables, X, Y, are said to be uncorrelated if their covariance, \operatorname ,Y= \operatorname Y- \operatorname \operatorname /math>, is zero. If two variables are uncorrelated, ther ...
at some time in the past; this allows for simple probabilistic treatment. This assumption is usually thought as a
boundary condition
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satis ...
, and thus the second law is ultimately a consequence of the initial conditions somewhere in the past, probably at the beginning of the universe (the
Big Bang
The Big Bang is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models based on the Big Bang concept explain a broad range of phenomena, including th ...
), though
other scenarios have also been suggested.
Given these assumptions, in statistical mechanics, the second law is not a postulate, rather it is a consequence of the
fundamental postulate, also known as the equal prior probability postulate, so long as one is clear that simple probability arguments are applied only to the future, while for the past there are auxiliary sources of information which tell us that it was low entropy. The first part of the second law, which states that the entropy of a thermally isolated system can only increase, is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of
is:
:
 The
The  The second law can be conceptually stated as follows: Matter and energy have the tendency to reach a state of uniformity or internal and external equilibrium, a state of maximum disorder (entropy). Real non-equilibrium processes always produce entropy, causing increased disorder in the universe, while idealized reversible processes produce no entropy and no process is known to exist that destroys entropy. The tendency of a system to approach uniformity may be counteracted, and the system may become more ordered or complex, by the combination of two things, a work or exergy source and some form of instruction or intelligence. Where 'exergy' is the thermal, mechanical, electric or chemical work potential of an energy source or flow, and 'instruction or intelligence', although subjective, is in the context of the set of category IV processes.
Consider a category IV example of robotic manufacturing and assembly of vehicles in a factory. The robotic machinery requires electrical work input and instructions, but when completed, the manufactured products have less uniformity with their surroundings, or more complexity (higher order) relative to the raw materials they were made from. Thus, system entropy or disorder decreases while the tendency towards uniformity between the system and its environment is counteracted. In this example, the instructions, as well as the source of work may be internal or external to the system, and they may or may not cross the system boundary. To illustrate, the instructions may be pre-coded and the electrical work may be stored in an energy storage system on-site. Alternatively, the control of the machinery may be by remote operation over a communications network, while the electric work is supplied to the factory from the local electric grid. In addition, humans may directly play, in whole or in part, the role that the robotic machinery plays in manufacturing. In this case, instructions may be involved, but intelligence is either directly responsible, or indirectly responsible, for the direction or application of work in such a way as to counteract the tendency towards disorder and uniformity.
There are also situations where the entropy spontaneously decreases by means of energy and entropy transfer. When thermodynamic constraints are not present, spontaneously energy or mass, as well as accompanying entropy, may be transferred out of a system in a progress to reach external equilibrium or uniformity in intensive properties of the system with its surroundings. This occurs spontaneously because the energy or mass transferred from the system to its surroundings results in a higher entropy in the surroundings, that is, it results in higher overall entropy of the system plus its surroundings. Note that this transfer of entropy requires dis-equilibrium in properties, such as a temperature difference. One example of this is the cooling crystallization of water that can occur when the system's surroundings are below freezing temperatures. Unconstrained heat transfer can spontaneously occur, leading to water molecules freezing into a crystallized structure of reduced disorder (sticking together in a certain order due to molecular attraction). The entropy of the system decreases, but the system approaches uniformity with its surroundings (category III).
On the other hand, consider the refrigeration of water in a warm environment. Due to refrigeration, as heat is extracted from the water, the temperature and entropy of the water decreases, as the system moves further away from uniformity with its warm surroundings or environment (category IV). The main point, take-away, is that refrigeration not only requires a source of work, it requires designed equipment, as well as pre-coded or direct operational intelligence or instructions to achieve the desired refrigeration effect.
The second law can be conceptually stated as follows: Matter and energy have the tendency to reach a state of uniformity or internal and external equilibrium, a state of maximum disorder (entropy). Real non-equilibrium processes always produce entropy, causing increased disorder in the universe, while idealized reversible processes produce no entropy and no process is known to exist that destroys entropy. The tendency of a system to approach uniformity may be counteracted, and the system may become more ordered or complex, by the combination of two things, a work or exergy source and some form of instruction or intelligence. Where 'exergy' is the thermal, mechanical, electric or chemical work potential of an energy source or flow, and 'instruction or intelligence', although subjective, is in the context of the set of category IV processes.
Consider a category IV example of robotic manufacturing and assembly of vehicles in a factory. The robotic machinery requires electrical work input and instructions, but when completed, the manufactured products have less uniformity with their surroundings, or more complexity (higher order) relative to the raw materials they were made from. Thus, system entropy or disorder decreases while the tendency towards uniformity between the system and its environment is counteracted. In this example, the instructions, as well as the source of work may be internal or external to the system, and they may or may not cross the system boundary. To illustrate, the instructions may be pre-coded and the electrical work may be stored in an energy storage system on-site. Alternatively, the control of the machinery may be by remote operation over a communications network, while the electric work is supplied to the factory from the local electric grid. In addition, humans may directly play, in whole or in part, the role that the robotic machinery plays in manufacturing. In this case, instructions may be involved, but intelligence is either directly responsible, or indirectly responsible, for the direction or application of work in such a way as to counteract the tendency towards disorder and uniformity.
There are also situations where the entropy spontaneously decreases by means of energy and entropy transfer. When thermodynamic constraints are not present, spontaneously energy or mass, as well as accompanying entropy, may be transferred out of a system in a progress to reach external equilibrium or uniformity in intensive properties of the system with its surroundings. This occurs spontaneously because the energy or mass transferred from the system to its surroundings results in a higher entropy in the surroundings, that is, it results in higher overall entropy of the system plus its surroundings. Note that this transfer of entropy requires dis-equilibrium in properties, such as a temperature difference. One example of this is the cooling crystallization of water that can occur when the system's surroundings are below freezing temperatures. Unconstrained heat transfer can spontaneously occur, leading to water molecules freezing into a crystallized structure of reduced disorder (sticking together in a certain order due to molecular attraction). The entropy of the system decreases, but the system approaches uniformity with its surroundings (category III).
On the other hand, consider the refrigeration of water in a warm environment. Due to refrigeration, as heat is extracted from the water, the temperature and entropy of the water decreases, as the system moves further away from uniformity with its warm surroundings or environment (category IV). The main point, take-away, is that refrigeration not only requires a source of work, it requires designed equipment, as well as pre-coded or direct operational intelligence or instructions to achieve the desired refrigeration effect.
 The first theory of the conversion of heat into mechanical work is due to
The first theory of the conversion of heat into mechanical work is due to  In 1865, the German physicist
In 1865, the German physicist