real projective plane on:
[Wikipedia]
[Google]
[Amazon]
In
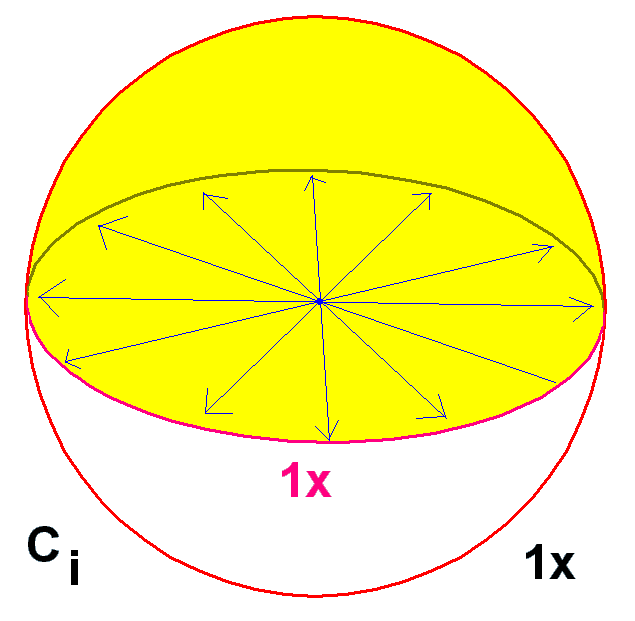 Because the sphere covers the real projective plane twice, the plane may be represented as a closed hemisphere around whose rim opposite points are identified.
Because the sphere covers the real projective plane twice, the plane may be represented as a closed hemisphere around whose rim opposite points are identified.
 A polyhedral representation is the tetrahemihexahedron, which has the same general form as Steiner's Roman surface, shown here.
A polyhedral representation is the tetrahemihexahedron, which has the same general form as Steiner's Roman surface, shown here.
Line field coloring using Werner Boy's real projective plane immersion
The real projective plane on YouTube
{{Compact topological surfaces Surfaces Geometric topology
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the real projective plane, denoted or , is a two-dimensional
A two-dimensional space is a mathematical space with two dimensions, meaning points have two degrees of freedom: their locations can be locally described with two coordinates or they can move in two independent directions. Common two-dimension ...
projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
, similar to the familiar Euclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
in many respects but without the concepts of distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
, circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
s, angle measure, or parallelism. It is the setting for planar projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
, in which the relationships between objects are not considered to change under projective transformations. The name ''projective'' comes from perspective drawing: projecting an image from one plane onto another as viewed from a point outside either plane, for example by photographing a flat painting from an oblique angle, is a projective transformation.
The fundamental objects in the projective plane are points and straight lines, and as in Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
, every pair of points determines a unique line passing through both, but unlike in the Euclidean case in projective geometry every pair of lines also determines a unique point at their intersection (in Euclidean geometry, parallel lines never intersect). In contexts where there is no ambiguity, it is simply called the projective plane; the qualifier "real" is added to distinguish it from other projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
s such as the complex projective plane
In mathematics, the complex projective plane, usually denoted or is the two-dimensional complex projective space. It is a complex manifold of complex dimension 2, described by three complex coordinates
:(Z_1,Z_2,Z_3) \in \C^3, \qquad (Z_1,Z_2, ...
and finite projective planes.
One common model of the real projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
is the space of lines in three-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
which pass through a particular origin point; in this model, lines through the origin are considered to be the "points" of the projective plane, and planes through the origin are considered to be the "lines" in the projective plane. These projective points and lines can be pictured in two dimensions by intersecting them with any arbitrary plane ''not'' passing through the origin; then the parallel plane which ''does'' pass through the origin (a projective "line") is called the line at infinity. (See below.)
In topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, the name ''real projective plane'' is applied to any surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
which is topologically equivalent to the real projective plane. Topologically, the real projective plane is compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
and non- orientable (one-sided). It cannot be embedded in three-dimensional Euclidean space without intersecting itself. It has Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's ...
1, hence a demigenus (non-orientable genus, Euler genus) of 1.
The topological real projective plane can be constructed by taking the (single) edge of a Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
and gluing it to itself in the correct direction, or by gluing the edge to a disk. Alternately, the real projective plane can be constructed by identifying each pair of opposite sides of the square, but in opposite directions, as shown in the diagram. (Performing any of these operations in three-dimensional space causes the surface to intersect itself.)
Examples
Projective geometry is not necessarily concerned with curvature and the real projective plane may be twisted up and placed in the Euclidean plane or 3-space in many different ways. Some of the more important examples are described below. The projective plane cannot be embedded (that is without intersection) in three-dimensionalEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. The proof that the projective plane does not embed in three-dimensional Euclidean space goes like this: Assuming that it does embed, it would bound a compact region in three-dimensional Euclidean space by the generalized Jordan curve theorem. The outward-pointing unit normal vector field would then give an orientation of the boundary manifold, but the boundary manifold would be the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
, which is not orientable. This is a contradiction, and so our assumption that it does embed must have been false.
The projective sphere
Consider asphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
, and let the great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
s of the sphere be "lines", and let pairs of antipodal points be "points". It is easy to check that this system obeys the axioms required of a projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
:
* any pair of distinct great circles meet at a pair of antipodal points; and
* any two distinct pairs of antipodal points lie on a single great circle.
If we identify each point on the sphere with its antipodal point, then we get a representation of the real projective plane in which the "points" of the projective plane really are points. This means that the projective plane is the quotient space of the sphere obtained by partitioning the sphere into equivalence classes under the equivalence relation ~, where if or . This quotient space of the sphere is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
with the collection of all lines passing through the origin in R3.
The quotient map from the sphere onto the real projective plane is in fact a two sheeted (i.e. two-to-one) covering map. It follows that the fundamental group of the real projective plane is the cyclic group of order 2; i.e., integers modulo 2. One can take the loop ''AB'' from the figure above to be the generator.
Projective hemisphere
 Because the sphere covers the real projective plane twice, the plane may be represented as a closed hemisphere around whose rim opposite points are identified.
Because the sphere covers the real projective plane twice, the plane may be represented as a closed hemisphere around whose rim opposite points are identified.
Boy's surface – an immersion
The projective plane can be immersed (local neighbourhoods of the source space do not have self-intersections) in 3-space.Boy's surface
In geometry, Boy's surface is an immersion of the real projective plane in three-dimensional space. It was discovered in 1901 by the German mathematician Werner Boy, who had been tasked by his doctoral thesis advisor David Hilbert to prove th ...
is an example of an immersion.
Polyhedral examples must have at least nine faces.
Roman surface
Steiner's Roman surface is a more degenerate map of the projective plane into 3-space, containing a cross-cap. A polyhedral representation is the tetrahemihexahedron, which has the same general form as Steiner's Roman surface, shown here.
A polyhedral representation is the tetrahemihexahedron, which has the same general form as Steiner's Roman surface, shown here.
Hemi polyhedra
Looking in the opposite direction, certain abstract regular polytopes – hemi-cube,hemi-dodecahedron
In geometry, a hemi-dodecahedron is an abstract polytope, abstract, regular polyhedron, containing half the Face (geometry), faces of a regular dodecahedron. It can be realized as a projective polyhedron (a tessellation of the real projective pla ...
, and hemi-icosahedron
In geometry, a hemi-icosahedron is an abstract polytope, abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), ...
– can be constructed as regular figures in the ''projective plane;'' see also projective polyhedra.
Planar projections
Various planar (flat) projections or mappings of the projective plane have been described. In 1874 Klein described the mapping: : Central projection of the projective hemisphere onto a plane yields the usual infinite projective plane, described below.Cross-capped disk
A closed surface is obtained by gluing a disk to a cross-cap. This surface can be represented parametrically by the following equations: : where both ''u'' and ''v'' range from 0 to 2''π''. These equations are similar to those of atorus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
. Figure 1 shows a closed cross-capped disk.
A cross-capped disk has a plane of symmetry that passes through its line segment of double points. In Figure 1 the cross-capped disk is seen from above its plane of symmetry ''z'' = 0, but it would look the same if seen from below.
A cross-capped disk can be sliced open along its plane of symmetry, while making sure not to cut along any of its double points. The result is shown in Figure 2.
Once this exception is made, it will be seen that the sliced cross-capped disk is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
to a self-intersecting disk, as shown in Figure 3.
The self-intersecting disk is homeomorphic to an ordinary disk. The parametric equations of the self-intersecting disk are:
:
where ''u'' ranges from 0 to 2''π'' and ''v'' ranges from 0 to 1.
Projecting the self-intersecting disk onto the plane of symmetry (''z'' = 0 in the parametrization given earlier) which passes only through the double points, the result is an ordinary disk which repeats itself (doubles up on itself).
The plane ''z'' = 0 cuts the self-intersecting disk into a pair of disks which are mirror reflections of each other. The disks have centers at the origin.
Now consider the rims of the disks (with ''v'' = 1). The points on the rim of the self-intersecting disk come in pairs which are reflections of each other with respect to the plane ''z'' = 0.
A cross-capped disk is formed by identifying these pairs of points, making them equivalent to each other. This means that a point with parameters (''u'', 1) and coordinates is identified with the point (''u'' + π, 1) whose coordinates are . But this means that pairs of opposite points on the rim of the (equivalent) ordinary disk are identified with each other; this is how a real projective plane is formed out of a disk. Therefore, the surface shown in Figure 1 (cross-cap with disk) is topologically equivalent to the real projective plane ''RP''2.
Homogeneous coordinates
The points in the plane can be represented byhomogeneous coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. ...
. A point has homogeneous coordinates 'x'' : ''y'' : ''z'' where the coordinates 'x'' : ''y'' : ''z''and 'tx'' : ''ty'' : ''tz''are considered to represent the same point, for all nonzero values of ''t''. The points with coordinates 'x'' : ''y'' : 1are the usual real plane, called the finite part of the projective plane, and points with coordinates 'x'' : ''y'' : 0 called points at infinity or ideal points, constitute a line called the line at infinity. (The homogeneous coordinates : 0 : 0do not represent any point.)
The lines in the plane can also be represented by homogeneous coordinates. A projective line corresponding to the plane in R3 has the homogeneous coordinates (''a'' : ''b'' : ''c''). Thus, these coordinates have the equivalence relation (''a'' : ''b'' : ''c'') = (''da'' : ''db'' : ''dc'') for all nonzero values of ''d''. Hence a different equation of the same line ''dax'' + ''dby'' + ''dcz'' = 0 gives the same homogeneous coordinates.
A point 'x'' : ''y'' : ''z''lies on a line (''a'' : ''b'' : ''c'') if ''ax'' + ''by'' + ''cz'' = 0.
Therefore, lines with coordinates (''a'' : ''b'' : ''c'') where ''a'', ''b'' are not both 0 correspond to the lines in the usual real plane, because they contain points that are not at infinity. The line with coordinates (0 : 0 : 1) is the line at infinity, since the only points on it are those with ''z'' = 0.
Points, lines, and planes
A line in P2 can be represented by the equation ''ax'' + ''by'' + ''cz'' = 0. If we treat ''a'', ''b'', and ''c'' as the column vector ℓ and ''x'', ''y'', ''z'' as the column vector x then the equation above can be written in matrix form as: : xTℓ = 0 or ℓTx = 0. Using vector notation we may instead write x ⋅ ℓ = 0 or ℓ ⋅ x = 0. The equation ''k''(xTℓ) = 0 (which k is a non-zero scalar) sweeps out a plane that goes through zero in R3 and ''k''(''x'') sweeps out a line, again going through zero. The plane and line arelinear subspace
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a ''function (mathematics), function'' (or ''mapping (mathematics), mapping'');
* linearity of a ''polynomial''.
An example of a li ...
s in R3, which always go through zero.
Ideal points
In P2 the equation of a line is and this equation can represent a line on any plane parallel to the ''x'', ''y'' plane by multiplying the equation by ''k''. If we have a normalized homogeneous coordinate. All points that have ''z'' = 1 create a plane. Let's pretend we are looking at that plane (from a position further out along the ''z'' axis and looking back towards the origin) and there are two parallel lines drawn on the plane. From where we are standing (given our visual capabilities) we can see only so much of the plane, which we represent as the area outlined in red in the diagram. If we walk away from the plane along the ''z'' axis, (still looking backwards towards the origin), we can see more of the plane. In our field of view original points have moved. We can reflect this movement by dividing the homogeneous coordinate by a constant. In the adjacent image we have divided by 2 so the ''z'' value now becomes 0.5. If we walk far enough away what we are looking at becomes a point in the distance. As we walk away we see more and more of the parallel lines. The lines will meet at a line at infinity (a line that goes through zero on the plane at ). Lines on the plane when are ideal points. The plane at is the line at infinity. The homogeneous point is where all the real points go when you're looking at the plane from an infinite distance, a line on the plane is where parallel lines intersect.Duality
In the equation there are twocolumn vector
In linear algebra, a column vector with elements is an m \times 1 matrix consisting of a single column of entries, for example,
\boldsymbol = \begin x_1 \\ x_2 \\ \vdots \\ x_m \end.
Similarly, a row vector is a 1 \times n matrix for some , c ...
s. You can keep either constant and vary the other. If we keep the point x constant and vary the coefficients ℓ we create new lines that go through the point. If we keep the coefficients constant and vary the points that satisfy the equation we create a line. We look upon x as a point, because the axes we are using are ''x'', ''y'', and ''z''. If we instead plotted the coefficients using axis marked ''a'', ''b'', ''c'' points would become lines and lines would become points. If you prove something with the data plotted on axis marked ''x'', ''y'', and ''z'' the same argument can be used for the data plotted on axis marked ''a'', ''b'', and ''c''. That is duality.
Lines joining points and intersection of lines (using duality)
The equation calculates theinner product
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, ofte ...
of two column vectors. The inner product of two vectors is zero if the vectors are orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
. In P2, the line between the points x1 and x2 may be represented as a column vector ℓ that satisfies the equations and , or in other words a column vector ℓ that is orthogonal to x1 and x2. The cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
will find such a vector: the line joining two points has homogeneous coordinates given by the equation . The intersection of two lines may be found in the same way, using duality, as the cross product of the vectors representing the lines, .
Embedding into 4-dimensional space
The projective plane embeds into 4-dimensional Euclidean space. The real projective plane P2(R) is the quotient of the two-sphere : S2 = by the antipodal relation . Consider the function given by . This map restricts to a map whose domain is S2 and, since each component is a homogeneous polynomial of even degree, it takes the same values in R4 on each of any two antipodal points on S2. This yields a map . Moreover, this map is an embedding. Notice that this embedding admits a projection into R3 which is the Roman surface.Higher non-orientable surfaces
By gluing together projective planes successively we get non-orientable surfaces of higher demigenus. The gluing process consists of cutting out a little disk from each surface and identifying (''gluing'') their boundary circles. Gluing two projective planes creates theKlein bottle
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the ...
.
The article on the fundamental polygon
In mathematics, a fundamental polygon can be defined for every compact Riemann surface of genus greater than 0. It encodes not only information about the topology of the surface through its fundamental group but also determines the Riemann surfa ...
describes the higher non-orientable surfaces.
See also
*Real projective space
In mathematics, real projective space, denoted or is the topological space of lines passing through the origin 0 in the real space It is a compact, smooth manifold of dimension , and is a special case of a Grassmannian space.
Basic properti ...
* Projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
* Pu's inequality for real projective plane
* Smooth projective plane
Citations
References
* * * * * *External links
*Line field coloring using Werner Boy's real projective plane immersion
The real projective plane on YouTube
{{Compact topological surfaces Surfaces Geometric topology