Point Group on:
[Wikipedia]
[Google]
[Amazon]
In
 The subset of pure reflectional point groups, defined by 1 or 2 mirrors, can also be given by their Coxeter group and related polygons. These include 5 crystallographic groups. The symmetry of the reflectional groups can be doubled by an
The subset of pure reflectional point groups, defined by 1 or 2 mirrors, can also be given by their Coxeter group and related polygons. These include 5 crystallographic groups. The symmetry of the reflectional groups can be doubled by an
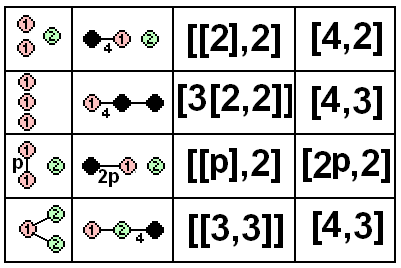 The reflection point groups, defined by 1 to 3 mirror planes, can also be given by their Coxeter group and related polyhedra. The ,3group can be doubled, written as , mapping the first and last mirrors onto each other, doubling the symmetry to 48, and isomorphic to the ,3group.
The reflection point groups, defined by 1 to 3 mirror planes, can also be given by their Coxeter group and related polyhedra. The ,3group can be doubled, written as , mapping the first and last mirrors onto each other, doubling the symmetry to 48, and isomorphic to the ,3group.
 The following list gives the four-dimensional reflection groups (excluding those that leave a subspace fixed and that are therefore lower-dimensional reflection groups). Each group is specified as a Coxeter group, and like the polyhedral groups of 3D, it can be named by its related convex regular 4-polytope. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3sup>+ has three 3-fold gyration points and symmetry order 60. Front-back symmetric groups like ,3,3and ,4,3can be doubled, shown as double brackets in Coxeter's notation, for example with its order doubled to 240.
The following list gives the four-dimensional reflection groups (excluding those that leave a subspace fixed and that are therefore lower-dimensional reflection groups). Each group is specified as a Coxeter group, and like the polyhedral groups of 3D, it can be named by its related convex regular 4-polytope. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3sup>+ has three 3-fold gyration points and symmetry order 60. Front-back symmetric groups like ,3,3and ,4,3can be doubled, shown as double brackets in Coxeter's notation, for example with its order doubled to 240.
 The following table gives the five-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3sup>+ has four 3-fold gyration points and symmetry order 360.
The following table gives the five-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3sup>+ has four 3-fold gyration points and symmetry order 360.
 The following table gives the six-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3,3sup>+ has five 3-fold gyration points and symmetry order 2520.
The following table gives the six-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3,3sup>+ has five 3-fold gyration points and symmetry order 2520.
** (Paper 23) H. S. M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559–591* H. S. M. Coxeter and W. O. J. Moser. ''Generators and Relations for Discrete Groups'' 4th ed, Springer-Verlag. New York. 1980 * N. W. Johnson: ''Geometries and Transformations'', (2018) Chapter 11: Finite symmetry groups
Web-based point group tutorial
(needs Java and Flash)
Subgroup enumeration
(needs Java)
* ttp://www.geom.uiuc.edu/docs/reference/CRC-formulas/node45.html The Geometry Center: 10.1 Formulas for Symmetries in Cartesian Coordinates (three dimensions) {{Authority control Crystallography Euclidean symmetries Group theory
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a point group is a mathematical group of symmetry operations ( isometries in a Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
) that have a fixed point in common. The coordinate origin
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter ''O'', used as a fixed point of reference for the geometry of the surrounding space.
In physical problems, the choice of origin is often arbitra ...
of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension ''d'' is then a subgroup of the orthogonal group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. ...
O(''d''). Point groups are used to describe the symmetries of geometric figures and physical objects such as molecules
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bio ...
.
Each point group can be represented as sets of orthogonal matrices ''M'' that transform point ''x'' into point ''y'' according to ''y'' = ''Mx''. Each element of a point group is either a rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional ...
(determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if a ...
of ''M'' = 1), or it is a reflection or improper rotation (determinant of ''M'' = −1).
The geometric symmetries of crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macro ...
s are described by space groups, which allow translations and contain point groups as subgroups. Discrete point groups in more than one dimension come in infinite families, but from the crystallographic restriction theorem and one of Bieberbach's theorems, each number of dimensions has only a finite number of point groups that are symmetric over some lattice or grid with that number of dimensions. These are the crystallographic point groups.
Chiral and achiral point groups, reflection groups
Point groups can be classified into '' chiral'' (or purely rotational) groups and ''achiral'' groups. The chiral groups are subgroups of the special orthogonal group SO(''d''): they contain only orientation-preserving orthogonal transformations, i.e., those of determinant +1. The achiral groups contain also transformations of determinant −1. In an achiral group, the orientation-preserving transformations form a (chiral) subgroup of index 2.Finite Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
s or ''reflection groups'' are those point groups that are generated purely by a set of reflectional mirrors passing through the same point. A rank ''n'' Coxeter group has ''n'' mirrors and is represented by a Coxeter-Dynkin diagram. Coxeter notation offers a bracketed notation equivalent to the Coxeter diagram, with markup symbols for rotational and other subsymmetry point groups. Reflection groups are necessarily achiral (except for the trivial group containing only the identity element).
List of point groups
One dimension
There are only two one-dimensional point groups, the identity group and the reflection group.Two dimensions
Point groups in two dimensions
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its ele ...
, sometimes called rosette groups.
They come in two infinite families:
# Cyclic groups ''C''''n'' of ''n''-fold rotation groups
# Dihedral groups ''D''''n'' of ''n''-fold rotation and reflection groups
Applying the crystallographic restriction theorem restricts ''n'' to values 1, 2, 3, 4, and 6 for both families, yielding 10 groups.
 The subset of pure reflectional point groups, defined by 1 or 2 mirrors, can also be given by their Coxeter group and related polygons. These include 5 crystallographic groups. The symmetry of the reflectional groups can be doubled by an
The subset of pure reflectional point groups, defined by 1 or 2 mirrors, can also be given by their Coxeter group and related polygons. These include 5 crystallographic groups. The symmetry of the reflectional groups can be doubled by an isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word i ...
, mapping both mirrors onto each other by a bisecting mirror, doubling the symmetry order.
Three dimensions
Point groups in three dimensions, sometimes called molecular point groups after their wide use in studying symmetries of molecules. They come in 7 infinite families of axial groups (also called prismatic), and 7 additional polyhedral groups (also called Platonic). In Schönflies notation, * Axial groups: C''n'', S2''n'', C''n''h, C''n''v, D''n'', D''n''d, D''n''h * Polyhedral groups: T, Td, Th, O, Oh, I, Ih Applying the crystallographic restriction theorem to these groups yields the 32 crystallographic point groups.Reflection groups
 The reflection point groups, defined by 1 to 3 mirror planes, can also be given by their Coxeter group and related polyhedra. The ,3group can be doubled, written as , mapping the first and last mirrors onto each other, doubling the symmetry to 48, and isomorphic to the ,3group.
The reflection point groups, defined by 1 to 3 mirror planes, can also be given by their Coxeter group and related polyhedra. The ,3group can be doubled, written as , mapping the first and last mirrors onto each other, doubling the symmetry to 48, and isomorphic to the ,3group.
Four dimensions
The four-dimensional point groups (chiral as well as achiral) are listed in Conway and Smith, Section 4, Tables 4.1-4.3. The following list gives the four-dimensional reflection groups (excluding those that leave a subspace fixed and that are therefore lower-dimensional reflection groups). Each group is specified as a Coxeter group, and like the polyhedral groups of 3D, it can be named by its related convex regular 4-polytope. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3sup>+ has three 3-fold gyration points and symmetry order 60. Front-back symmetric groups like ,3,3and ,4,3can be doubled, shown as double brackets in Coxeter's notation, for example with its order doubled to 240.
The following list gives the four-dimensional reflection groups (excluding those that leave a subspace fixed and that are therefore lower-dimensional reflection groups). Each group is specified as a Coxeter group, and like the polyhedral groups of 3D, it can be named by its related convex regular 4-polytope. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3sup>+ has three 3-fold gyration points and symmetry order 60. Front-back symmetric groups like ,3,3and ,4,3can be doubled, shown as double brackets in Coxeter's notation, for example with its order doubled to 240.
Five dimensions
 The following table gives the five-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3sup>+ has four 3-fold gyration points and symmetry order 360.
The following table gives the five-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3sup>+ has four 3-fold gyration points and symmetry order 360.
Six dimensions
 The following table gives the six-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3,3sup>+ has five 3-fold gyration points and symmetry order 2520.
The following table gives the six-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3,3sup>+ has five 3-fold gyration points and symmetry order 2520.
Seven dimensions
The following table gives the seven-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3,3,3sup>+ has six 3-fold gyration points and symmetry order 20160.Eight dimensions
The following table gives the eight-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example ,3,3,3,3,3,3sup>+ has seven 3-fold gyration points and symmetry order 181440.See also
*Point groups in two dimensions
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its ele ...
* Point groups in three dimensions
*Point groups in four dimensions
In geometry, a point group in four dimensions is an isometry group in four dimensions that leaves the origin fixed, or correspondingly, an isometry group of a 3-sphere.
History on four-dimensional groups
* 1889 Édouard Goursat, ''Sur les su ...
* Crystallography
* Crystallographic point group
*Molecular symmetry
Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain m ...
* Space group
* X-ray diffraction
*Bravais lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n ...
* Infrared spectroscopy of metal carbonyls
References
Further reading
*H. S. M. Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington t ...
: ''Kaleidoscopes: Selected Writings of H. S. M. Coxeter'', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,** (Paper 23) H. S. M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559–591* H. S. M. Coxeter and W. O. J. Moser. ''Generators and Relations for Discrete Groups'' 4th ed, Springer-Verlag. New York. 1980 * N. W. Johnson: ''Geometries and Transformations'', (2018) Chapter 11: Finite symmetry groups
External links
Web-based point group tutorial
(needs Java and Flash)
Subgroup enumeration
(needs Java)
* ttp://www.geom.uiuc.edu/docs/reference/CRC-formulas/node45.html The Geometry Center: 10.1 Formulas for Symmetries in Cartesian Coordinates (three dimensions) {{Authority control Crystallography Euclidean symmetries Group theory