pink noise

Pink noise, noise, fractional noise or fractal noise is a signal or process with a frequency spectrum such that the power spectral density (power per frequency interval) is inversely proportional to the frequency of the signal. In pink noise, each octave interval (halving or doubling in frequency) carries an equal amount of noise energy.

Pink noise sounds like a waterfall. It is often used to tune loudspeaker systems in professional audio. Pink noise is one of the most commonly observed signals in biological systems.

The name arises from the pink appearance of visible light with this power spectrum. This is in contrast with white noise which has equal intensity per frequency interval.

Definition

Within the scientific literature, the term "1/f noise" is sometimes used loosely to refer to any noise with a power spectral density of the form

$S(f) \propto \frac,$

where is frequency, and , with exponent usually close to 1. One-dimensional signals with are usually called pink noise.

The following function describes a length one-dimensional pink noise signal (i.e. a Gaussian white noise signal with zero mean and standard deviation , which has been suitably filtered), as a sum of sine waves with different frequencies, whose amplitudes fall off inversely with the square root of frequency (so that power, which is the square of amplitude, falls off inversely with frequency), and phases are random:

$h(x)=\sigma \sqrt \sum_u \frac \sin \left( \frac +\phi_u \right), \quad \chi_u \sim \chi(2), \quad \phi_u \sim U(0,2\pi).$

are independently and identically () chi-distributed variables, and are uniform random.

In a two-dimensional pink noise signal, the amplitude at any orientation falls off inversely with frequency. A pink noise square of length can be written as:
$h(x,y)= \frac \sum_ \frac \sin \left(\frac(ux+vy) +\phi_ \right), \quad \chi_ \sim \chi(2), \quad \phi_ \sim U(0,2\pi).$

General -like noises occur widely in nature and are a source of considerable interest in many fields. Noises with near 1 generally come from condensed-matter systems in quasi-equilibrium, as discussed below. Noises with a broad range of generally correspond to a wide range of non-equilibrium driven dynamical systems.

Pink noise sources include '' flicker noise'' in electronic devices. In their study of fractional Brownian motion, Mandelbrot and Van Ness proposed the name ''fractional noise'' (sometimes since called ''fractal noise'') to describe noises for which the exponent is not an even integer, or that are fractional derivatives of Brownian () noise.

Description

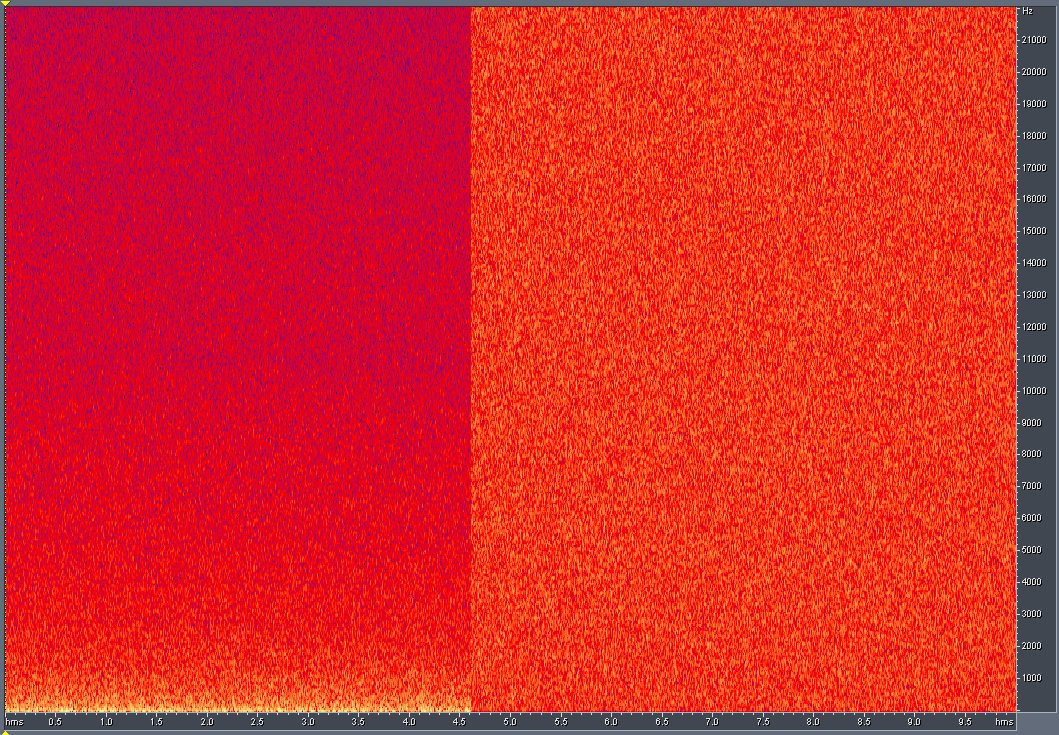
In pink noise, there is equal energy per octave of frequency. The energy of pink noise at each frequency level, however, falls off at roughly 3  dB per octave. This is in contrast to white noise which has equal energy at all frequency levels.

The human auditory system, which processes frequencies in a roughly logarithmic fashion approximated by the Bark scale, does not perceive different frequencies with equal sensitivity; signals around 1–4 kHz sound loudest for a given intensity. However, humans still differentiate between white noise and pink noise with ease.

Graphic equalizers also divide signals into bands logarithmically and report power by octaves; audio engineers put pink noise through a system to test whether it has a flat frequency response in the spectrum of interest. Systems that do not have a flat response can be equalized by creating an inverse filter using a graphic equalizer. Because pink noise tends to occur in natural physical systems, it is often useful in audio production. Pink noise can be processed, filtered, and/or effects can be added to produce desired sounds. Pink-noise generators are commercially available.

One parameter of noise, the peak versus average energy contents, or crest factor, is important for testing purposes, such as for audio power amplifier and loudspeaker capabilities because the signal power is a direct function of the crest factor. Various crest factors of pink noise can be used in simulations of various levels of dynamic range compression in music signals. On some digital pink-noise generators the crest factor can be specified.

Generation

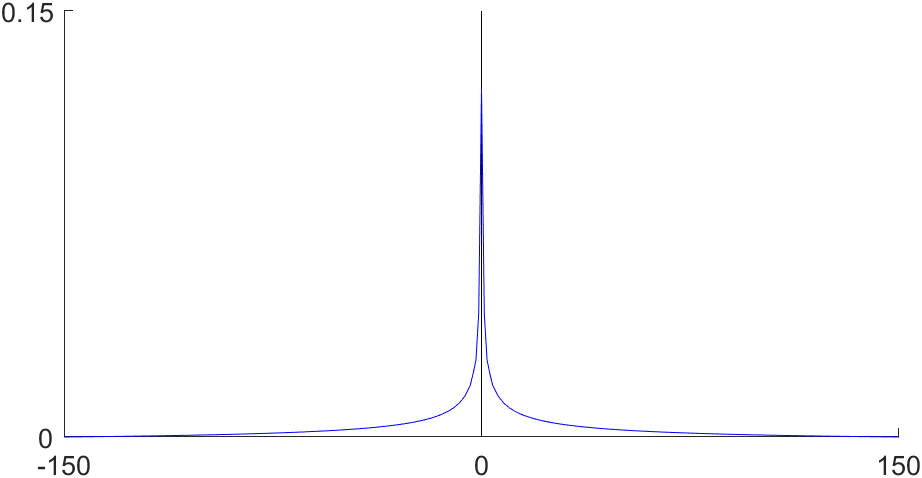
Pink noise can be computer-generated by first generating a white noise signal, Fourier-transforming it, then dividing the amplitudes of the different frequency components by the square root of the frequency (in one dimension), or by the frequency (in two dimensions) etc. This is equivalent to spatially filtering (convolving) the white noise signal with a white-to-pink-filter. For a length $N$ signal in one dimension, the filter has the following form:

a(x)=\frac \left 1+ \frac \cos \pi (x-1) + 2 \sum_^ \frac \cos \right

Matlab programs are available to generate pink and other power-law coloured noise i
one
or
any number
of dimensions.

Properties

Power-law spectra

The power spectrum of pink noise is $\frac$ only for one-dimensional signals. For two-dimensional signals (e.g., images) the average power spectrum at any orientation falls as $\frac$, and in $d$ dimensions, it falls as $\frac$. In every case, each octave carries an equal amount of noise power.

The average amplitude $a_\theta$ and power $p_\theta$ of a pink noise signal at any orientation $\theta$, and the total power across all orientations, fall off as some power of the frequency. The following table lists these power-law frequency-dependencies for pink noise signal in different dimensions, and also for general power-law colored noise with power $\alpha$ (e.g.: Brown noise has $\alpha=2$):

Distribution of point values

Consider pink noise of any dimension that is produced by generating a Gaussian white noise signal with mean $\mu$ and sd $\sigma$, then multiplying its spectrum with a filter (equivalent to spatially filtering it with a filter $\boldsymbol$). Then the point values of the pink noise signal will also be normally distributed, with mean $\mu$ and sd $\lVert \boldsymbol \rVert \sigma$.

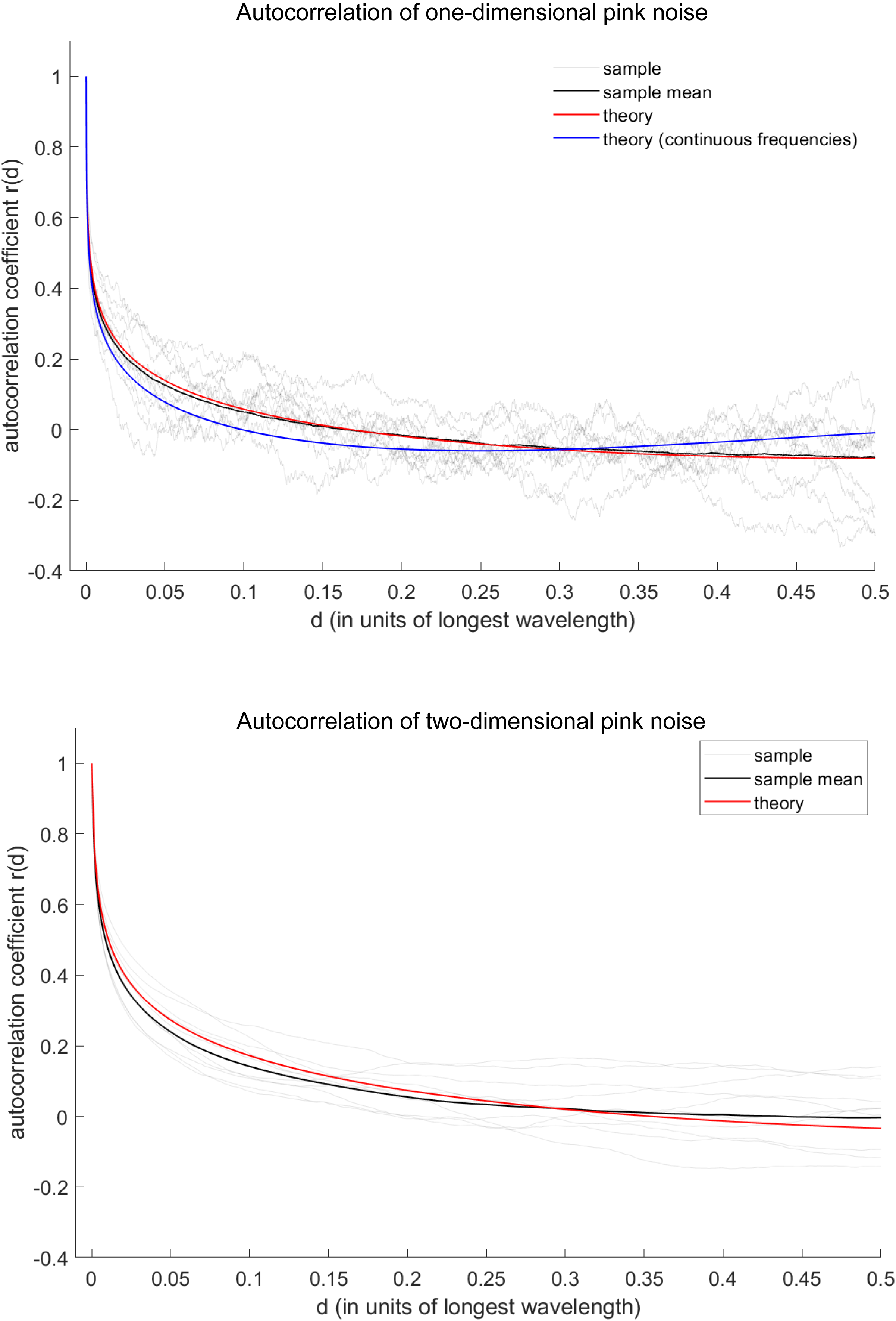
Autocorrelation

Unlike white noise, which has no correlations across the signal, a pink noise signal is correlated with itself, as follows.

1D signal

The Pearson's correlation coefficient of a one-dimensional pink noise signal (comprising discrete frequencies $k$) with itself across a distance $d$ in the configuration (space or time) domain is:
$r(d)=\frac.$
If instead of discrete frequencies, the pink noise comprises a superposition of continuous frequencies from $k_\textrm$ to $k_\textrm$, the autocorrelation coefficient is:
$r(d)=\frac,$
where $\textrm(x)$ is the cosine integral function.

2D signal

The Pearson's autocorrelation coefficient of a two-dimensional pink noise signal comprising discrete frequencies is theoretically approximated as:
$r(d)=\frac,$
where $J_0$ is the Bessel function of the first kind.

Occurrence

Pink noise has been discovered in the statistical fluctuations of an extraordinarily diverse number of physical and biological systems (Press, 1978; see articles in Handel & Chung, 1993, and references therein). Examples of its occurrence include fluctuations in tide and river heights, quasar light emissions, heart beat, firings of single neurons, resistivity in solid-state electronics and single-molecule conductance signals resulting in flicker noise. Pink noise describes the statistical structure of many natural images.

General 1/''f'' ^α noises occur in many physical, biological and economic systems, and some researchers describe them as being ubiquitous. In physical systems, they are present in some meteorological data series, the electromagnetic radiation output of some astronomical bodies. In biological systems, they are present in, for example, heart beat rhythms, neural activity, and the statistics of DNA sequences, as a generalized pattern.

An accessible introduction to the significance of pink noise is one given by Martin Gardner (1978) in his ''Scientific American'' column "Mathematical Games". In this column, Gardner asked for the sense in which music imitates nature. Sounds in nature are not musical in that they tend to be either too repetitive (bird song, insect noises) or too chaotic (ocean surf, wind in trees, and so forth). The answer to this question was given in a statistical sense by Voss and Clarke (1975, 1978), who showed that pitch and loudness fluctuations in speech and music are pink noises. So music is like tides not in terms of how tides sound, but in how tide heights vary.

Precision timekeeping

The ubiquitous 1/f noise poses a "noise floor" to precision timekeeping. The derivation is based on.

Suppose that we have a timekeeping device (it could be anything from quartz oscillators, atomic clocks, and hourglasses). Let its readout be a real number $x(t)$ that changes with the actual time $t$. For concreteness, let us consider a quartz oscillator. In a quartz oscillator, $x(t)$ is the number of oscillations, and $\dot x(t)$ is the rate of oscillation. The rate of oscillation has a constant component $\dot x_0$and a fluctuating component $\dot x_f$, so $\dot x(t) = \dot x_0 + \dot x_f(t)$. By selecting the right units for $x$, we can have $\dot x_0 = 1$, meaning that on average, one second of clock-time passes for every second of real-time.

The stability of the clock is measured by how many "ticks" it makes over a fixed interval. The more stable the number of ticks, the better the stability of the clock. So, define the average clock frequency over the interval \tau, (k+1)\tau/math> as$y_k = \frac\int_^\dot x(t)dt = \frac$Note that $y_k$ is unitless: it is the numerical ratio between ticks of the physical clock and ticks of an ideal clock.

The Allan variance of the clock frequency is half the mean square of change in average clock frequency:$\sigma^2(\tau) = \frac 12 \overline = \frac\sum_^K \frac 12 (y_ - y_)^2$where $K$ is an integer large enough for the averaging to converge to a definite value.
For example, a 2013 atomic clock achieved $\sigma(25000\text) = 1.6 \times 10^$, meaning that if the clock is used to repeatedly measure intervals of 7 hours, the standard deviation of the actually measured time would be around 40 femtoseconds.

Now we have$y_ - y_ = \int_\R g(k\tau - t) \dot x_f(t) dt = (g\ast \dot x_f)(k\tau)$where $g(t) = \frac$ is one packet of a square wave with height $1/\tau$ and wavelength $2\tau$. Let $h(t)$ be a packet of a square wave with height 1 and wavelength 2, then $g(t) = h(t/\tau)/\tau$, and its Fourier transform satisfies \mathcal F \omega) = \mathcal F \tau\omega).

The Allan variance is then $\sigma^2(\tau) = \frac 12 \overline = \frac 12 \overline$, and the discrete averaging can be approximated by a continuous averaging: $\frac\sum_^K \frac 12 (y_ - y_)^2 \approx \frac\int_0^ \frac 12(g\ast \dot x_f)(t)^2 dt$, which is the total power of the signal $(g\ast \dot x_f)$, or the integral of its power spectrum:

\sigma^2(\tau) \approx \int_0^\infty S \ast \dot x_f\omega) d\omega = \int_0^\infty S \omega) \cdot S dot x_f\omega) d\omega = \int_0^\infty S \tau \omega) \cdot S dot x_f\omega) d\omegaIn words, the Allan variance is approximately the power of the fluctuation after bandpass filtering at $\omega \sim 1/\tau$ with bandwidth $\Delta\omega \sim 1/\tau$.

For $1/f^\alpha$ fluctuation, we have S dot x_f\omega) = C/\omega^\alpha for some constant $C$, so $\sigma^2(\tau) \approx \tau^ \sigma^2(1) \propto \tau^$. In particular, when the fluctuating component $\dot x_f$ is a 1/f noise, then $\sigma^2(\tau)$ is independent of the averaging time $\tau$, meaning that the clock frequency does not become more stable by simply averaging for longer. This contrasts with a white noise fluctuation, in which case $\sigma^2(\tau) \propto \tau^$, meaning that doubling the averaging time would improve the stability of frequency by $\sqrt 2$.

The cause of the noise floor is often traced to particular electronic components (such as transistors, resistors, and capacitors) within the oscillator feedback.

Humans

In brains, pink noise has been widely observed across many temporal and physical scales from ion channel gating to EEG and MEG and LFP recordings in humans. In clinical EEG, deviations from this 1/f pink noise can be used to identify epilepsy, even in the absence of a seizure, or during the interictal state. Classic models of EEG generators suggested that dendritic inputs in gray matter were principally responsible for generating the 1/f power spectrum observed in EEG/MEG signals. However, recent computational models using cable theory have shown that action potential transduction along white matter tracts in the brain also generates a 1/f spectral density. Therefore, white matter signal transduction may also contribute to pink noise measured in scalp EEG recordings,
particularly if the effects of ephaptic coupling are taken into consideration.

It has also been successfully applied to the modeling of mental states in psychology, and used to explain stylistic variations in music from different cultures and historic periods. Richard F. Voss and J. Clarke claim that almost all musical melodies, when each successive note is plotted on a scale of pitches, will tend towards a pink noise spectrum. Similarly, a generally pink distribution pattern has been observed in film shot length by researcher James E. Cutting of Cornell University, in the study of 150 popular movies released from 1935 to 2005.

Pink noise has also been found to be endemic in human response. Gilden et al. (1995) found extremely pure examples of this noise in the time series formed upon iterated production of temporal and spatial intervals. Later, Gilden (1997) and Gilden (2001) found that time series formed from reaction time measurement and from iterated two-alternative forced choice also produced pink noises.

Electronic devices

The principal sources of pink noise in electronic devices are almost invariably the slow fluctuations of properties of the condensed-matter materials of the devices. In many cases the specific sources of the fluctuations are known. These include fluctuating configurations of defects in metals, fluctuating occupancies of traps in semiconductors, and fluctuating domain structures in magnetic materials. The explanation for the approximately pink spectral form turns out to be relatively trivial, usually coming from a distribution of kinetic activation energies of the fluctuating processes. Since the frequency range of the typical noise experiment (e.g., 1 Hz – 1 kHz) is low compared with typical microscopic "attempt frequencies" (e.g., 10¹⁴ Hz), the exponential factors in the Arrhenius equation for the rates are large. Relatively small spreads in the activation energies appearing in these exponents then result in large spreads of characteristic rates. In the simplest toy case, a flat distribution of activation energies gives exactly a pink spectrum, because $\textstyle \frac\ln f = \frac.$

There is no known lower bound to background pink noise in electronics. Measurements made down to 10⁻⁶ Hz (taking several weeks) have not shown a ceasing of pink-noise behaviour. (Kleinpenning, de Kuijper, 1988) measured the resistance in a noisy carbon-sheet resistor, and found 1/f noise behavior over the range of 0^ \mathrm, 10^4 \mathrm/math>, a range of 9.5 decades.

A pioneering researcher in this field was Aldert van der Ziel.

Flicker noise is commonly used for the reliability characterization of electronic devices. It is also used for gas detection in chemoresistive sensors by dedicated measurement setups.

In gravitational wave astronomy

1/''f'' ^α noises with α near 1 are a factor in gravitational-wave astronomy. The noise curve at very low frequencies affects pulsar timing arrays, the European Pulsar Timing Array (EPTA) and the future International Pulsar Timing Array (IPTA); at low frequencies are space-borne detectors, the formerly proposed Laser Interferometer Space Antenna (LISA) and the currently proposed evolved Laser Interferometer Space Antenna (eLISA), and at high frequencies are ground-based detectors, the initial Laser Interferometer Gravitational-Wave Observatory (LIGO) and its advanced configuration (aLIGO). The characteristic strain of potential astrophysical sources are also shown. To be detectable the characteristic strain of a signal must be above the noise curve.

Climate dynamics

Pink noise on timescales of decades has been found in climate proxy data, which may indicate amplification and coupling of processes in the climate system.

Diffusion processes

Many time-dependent stochastic processes are known to exhibit 1/''f'' ^α noises with α between 0 and 2. In particular Brownian motion has a power spectral density that equals 4''D''/''f'' ², where ''D'' is the diffusion coefficient. This type of spectrum is sometimes referred to as Brownian noise. The analysis of individual Brownian motion trajectories also show 1/''f'' ² spectrum, albeit with random amplitudes. Fractional Brownian motion with Hurst exponent ''H'' also show 1/''f'' ^α power spectral density with α=2''H''+1 for subdiffusive processes (''H''<0.5) and α=2 for superdiffusive processes (0.5<''H''<1).

Origin

There are many theories about the origin of pink noise. Some theories attempt to be universal, while others apply to only a certain type of material, such as semiconductors. Universal theories of pink noise remain a matter of current research interest.

A hypothesis (referred to as the Tweedie hypothesis) has been proposed to explain the genesis of pink noise on the basis of a mathematical convergence theorem related to the central limit theorem of statistics. The Tweedie convergence theorem describes the convergence of certain statistical processes towards a family of statistical models known as the Tweedie distributions. These distributions are characterized by a variance to mean power law, that have been variously identified in the ecological literature as Taylor's law and in the physics literature as ''fluctuation scaling''. When this variance to mean power law is demonstrated by the method of expanding enumerative bins this implies the presence of pink noise, and vice versa. Both of these effects can be shown to be the consequence of mathematical convergence such as how certain kinds of data will converge towards the normal distribution under the central limit theorem. This hypothesis also provides for an alternative paradigm to explain power law manifestations that have been attributed to self-organized criticality.

There are various mathematical models to create pink noise. The superposition of exponentially decaying pulses is able to generate a signal with the $1/f$-spectrum at moderate frequencies, transitioning to a constant at low frequencies and $1/f^2$ at high frequencies. In contrast, the sandpile model of self-organized criticality, which exhibits quasi-cycles of gradual stress accumulation between fast rare stress-releases, reproduces the flicker noise that corresponds to the intra-cycle dynamics. The statistical signature of self-organization is justified in It can be generated on computer, for example, by filtering white noise, inverse Fourier transform, or by multirate variants on standard white noise generation.

In supersymmetric theory of stochastics, an approximation-free theory of stochastic differential equations, 1/''f'' noise is one of the manifestations of the spontaneous breakdown of topological supersymmetry. This supersymmetry is an intrinsic property of all stochastic differential equations and its meaning is the preservation of the continuity of the phase space by continuous time dynamics. Spontaneous breakdown of this supersymmetry is the stochastic generalization of the concept of deterministic chaos, whereas the associated emergence of the long-term dynamical memory or order, i.e., 1/''f'' and crackling noises, the Butterfly effect etc., is the consequence of the Goldstone theorem in the application to the spontaneously broken topological supersymmetry.

Audio testing

Pink noise is commonly used to test the loudspeakers in sound reinforcement systems, with the resulting sound measured with a test microphone in the listening space connected to a spectrum analyzer or a computer running a real-time fast Fourier transform (FFT) analyzer program such as Smaart. The sound system plays pink noise while the audio engineer makes adjustments on an audio equalizer to obtain the desired results. Pink noise is predictable and repeatable, but it is annoying for a concert audience to hear. Since the late 1990s, FFT-based analysis enabled the engineer to make adjustments using pre-recorded music as the test signal, or even the music coming from the performers in real time. Pink noise is still used by audio system contractors and by computerized sound systems which incorporate an automatic equalization feature.

In manufacturing, pink noise is often used as a burn-in signal for audio amplifiers and other components, to determine whether the component will maintain performance integrity during sustained use. The process of end-users burning in their headphones with pink noise to attain higher fidelity has been called an audiophile "myth".

See also

* Architectural acoustics
* Audio signal processing
* Brownian noise
* White noise
* Colors of noise
* Crest factor
* Fractal
* Flicker noise
* Johnson–Nyquist noise
* Noise (electronics)
* Quantum 1/f noise
* Self-organised criticality
* Shot noise
* Sound masking
* Statistics

Footnotes

References

*
*
*
*
*
*
*
*
*
*
*

External links

Coloured Noise: Matlab toolbox to generate power-law coloured noise signals of any dimensions.

Powernoise: Matlab software for generating 1/''f'' noise, or more generally, 1/''f''^α noise

1/f noise at Scholarpedia

White Noise Definition Vs Pink Noise

{{DEFAULTSORT:Pink Noise

Noise (electronics)
Sound
Acoustics