orientation (vector space) on:
[Wikipedia]
[Google]
[Amazon]
 The orientation of a real vector space or simply orientation of a vector space is the arbitrary choice of which ordered bases are "positively" oriented and which are "negatively" oriented. In the three-dimensional
The orientation of a real vector space or simply orientation of a vector space is the arbitrary choice of which ordered bases are "positively" oriented and which are "negatively" oriented. In the three-dimensional
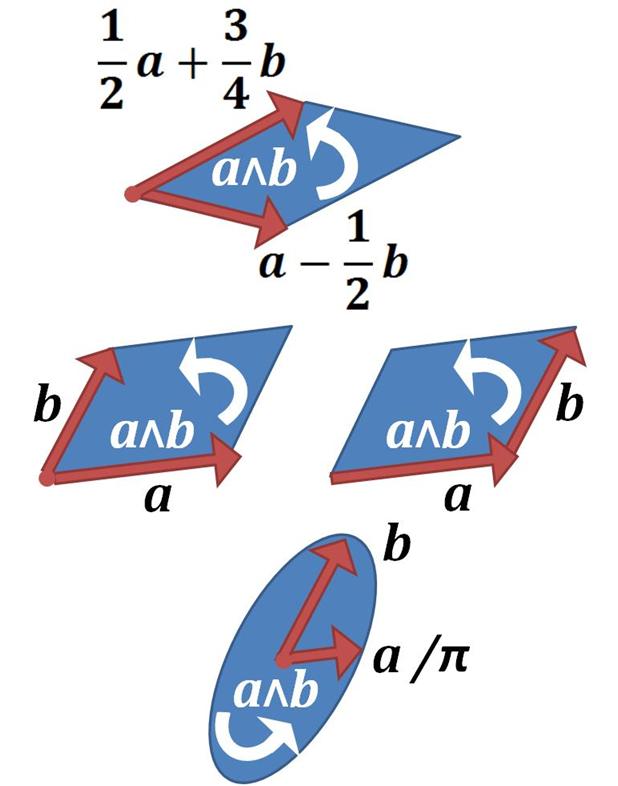 The various objects of geometric algebra are charged with three attributes or ''features'': attitude, orientation, and magnitude.
For example, a vector has an attitude given by a straight line parallel to it, an orientation given by its sense (often indicated by an arrowhead) and a magnitude given by its length. Similarly, a bivector in three dimensions has an attitude given by the family of planes associated with it (possibly specified by the normal line common to these planes
), an orientation (sometimes denoted by a curved arrow in the plane) indicating a choice of sense of traversal of its boundary (its ''circulation''), and a magnitude given by the area of the parallelogram defined by its two vectors.
The various objects of geometric algebra are charged with three attributes or ''features'': attitude, orientation, and magnitude.
For example, a vector has an attitude given by a straight line parallel to it, an orientation given by its sense (often indicated by an arrowhead) and a magnitude given by its length. Similarly, a bivector in three dimensions has an attitude given by the family of planes associated with it (possibly specified by the normal line common to these planes
), an orientation (sometimes denoted by a curved arrow in the plane) indicating a choice of sense of traversal of its boundary (its ''circulation''), and a magnitude given by the area of the parallelogram defined by its two vectors.
Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, right-handed bases are typically declared to be positively oriented, but the choice is arbitrary, as they may also be assigned a negative orientation. A vector space with an orientation selected is called an oriented vector space, while one not having an orientation selected, is called .
In mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, '' orientability'' is a broader notion that, in two dimensions, allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra over the real numbers, the notion of orientation makes sense in arbitrary finite dimension, and is a kind of asymmetry that makes a reflection impossible to replicate by means of a simple displacement. Thus, in three dimensions, it is impossible to make the left hand of a human figure into the right hand of the figure by applying a displacement alone, but it is possible to do so by reflecting the figure in a mirror. As a result, in the three-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, the two possible basis orientations are called right-handed and left-handed (or right-chiral and left-chiral).
Definition
Let ''V'' be a finite-dimensional real vector space and let ''b''1 and ''b''2 be two ordered bases for ''V''. It is a standard result in linear algebra that there exists a unique linear transformation ''A'' : ''V'' → ''V'' that takes ''b''1 to ''b''2. The bases ''b''1 and ''b''2 are said to have the ''same orientation'' (or be consistently oriented) if ''A'' has positivedeterminant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
; otherwise they have ''opposite orientations''. The property of having the same orientation defines an equivalence relation on the set of all ordered bases for ''V''. If ''V'' is non-zero, there are precisely two equivalence classes determined by this relation. An orientation on ''V'' is an assignment of +1 to one equivalence class and −1 to the other.
Every ordered basis lives in one equivalence class or another. Thus any choice of a privileged ordered basis for ''V'' determines an orientation: the orientation class of the privileged basis is declared to be positive.
For example, the standard basis on R''n'' provides a standard orientation on R''n'' (in turn, the orientation of the standard basis depends on the orientation of the Cartesian coordinate system on which it is built). Any choice of a linear isomorphism between ''V'' and R''n'' will then provide an orientation on ''V''.
The ordering of elements in a basis is crucial. Two bases with a different ordering will differ by some permutation. They will have the same/opposite orientations according to whether the signature of this permutation is ±1. This is because the determinant of a permutation matrix is equal to the signature of the associated permutation.
Similarly, let ''A'' be a nonsingular linear mapping of vector space R''n'' to R''n''. This mapping is orientation-preserving if its determinant is positive. For instance, in R3 a rotation around the ''Z'' Cartesian axis by an angle ''α'' is orientation-preserving:
while a reflection by the ''XY'' Cartesian plane is not orientation-preserving:
Zero-dimensional case
The concept of orientation degenerates in the zero-dimensional case. A zero-dimensional vector space has only a single point, the zero vector. Consequently, the only basis of a zero-dimensional vector space is the empty set . Therefore, there is a single equivalence class of ordered bases, namely, the class whose sole member is theempty set
In mathematics, the empty set or void set is the unique Set (mathematics), set having no Element (mathematics), elements; its size or cardinality (count of elements in a set) is 0, zero. Some axiomatic set theories ensure that the empty set exi ...
. This means that an orientation of a zero-dimensional space is a function
It is therefore possible to orient a point in two different ways, positive and negative.
Because there is only a single ordered basis , a zero-dimensional vector space is the same as a zero-dimensional vector space with ordered basis. Choosing or therefore chooses an orientation of every basis of every zero-dimensional vector space. If all zero-dimensional vector spaces are assigned this orientation, then, because all isomorphisms among zero-dimensional vector spaces preserve the ordered basis, they also preserve the orientation. This is unlike the case of higher-dimensional vector spaces where there is no way to choose an orientation so that it is preserved under all isomorphisms.
However, there are situations where it is desirable to give different orientations to different points. For example, consider the fundamental theorem of calculus as an instance of Stokes' theorem. A closed interval is a one-dimensional manifold with boundary, and its boundary is the set . In order to get the correct statement of the fundamental theorem of calculus, the point should be oriented positively, while the point should be oriented negatively.
On a line
The one-dimensional case deals with an oriented line or directed line, which may be traversed in one of two directions. In real coordinate space, an oriented line is also known as an ''axis''. There are two orientations to a line just as there are two orientations to an oriented circle (clockwise and anti-clockwise). A semi-infinite oriented line is called a '' ray''. In the case of a line segment (a connected subset of a line), the two possible orientations result in '' directed line segments''.On a surface
An orientable surface sometimes has the selected orientation indicated by the orientation of a surface normal. An oriented plane can be defined by a pseudovector.Alternate viewpoints
Multilinear algebra
For any ''n''-dimensional real vector space ''V'' we can form the ''k''th- exterior power of ''V'', denoted Λ''k''''V''. This is a real vector space of dimension . The vector space Λ''n''''V'' (called the ''top exterior power'') therefore has dimension 1. That is, Λ''n''''V'' is just a real line. There is no ''a priori'' choice of which direction on this line is positive. An orientation is just such a choice. Any nonzero linear form ''ω'' on Λ''n''''V'' determines an orientation of ''V'' by declaring that ''x'' is in the positive direction when ''ω''(''x'') > 0. To connect with the basis point of view we say that the positively-oriented bases are those on which ''ω'' evaluates to a positive number (since ''ω'' is an ''n''-form we can evaluate it on an ordered set of ''n'' vectors, giving an element of R). The form ''ω'' is called an orientation form. If is a privileged basis for ''V'' and is the dual basis, then the orientation form giving the standard orientation is . The connection of this with the determinant point of view is: the determinant of an endomorphism can be interpreted as the induced action on the top exterior power.Lie group theory
Let ''B'' be the set of all ordered bases for ''V''. Then thegeneral linear group
In mathematics, the general linear group of degree n is the set of n\times n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again inve ...
GL(''V'') acts freely and transitively on ''B''. (In fancy language, ''B'' is a GL(''V'')- torsor). This means that as a manifold, ''B'' is (noncanonically) homeomorphic to GL(''V''). Note that the group GL(''V'') is not connected, but rather has two connected components according to whether the determinant of the transformation is positive or negative (except for GL0, which is the trivial group and thus has a single connected component; this corresponds to the canonical orientation on a zero-dimensional vector space). The identity component of GL(''V'') is denoted GL+(''V'') and consists of those transformations with positive determinant. The action of GL+(''V'') on ''B'' is ''not'' transitive: there are two orbits which correspond to the connected components of ''B''. These orbits are precisely the equivalence classes referred to above. Since ''B'' does not have a distinguished element (i.e. a privileged basis) there is no natural choice of which component is positive. Contrast this with GL(''V'') which does have a privileged component: the component of the identity. A specific choice of homeomorphism between ''B'' and GL(''V'') is equivalent to a choice of a privileged basis and therefore determines an orientation.
More formally: ,
and the Stiefel manifold of ''n''-frames in is a - torsor, so is a torsor over , i.e., its 2 points, and a choice of one of them is an orientation.
Geometric algebra
Orientation on manifolds
Each point ''p'' on an ''n''-dimensional differentiable manifold has a tangent space ''T''''p''''M'' which is an ''n''-dimensional real vector space. Each of these vector spaces can be assigned an orientation. Some orientations "vary smoothly" from point to point. Due to certain topological restrictions, this is not always possible. A manifold that admits a smooth choice of orientations for its tangent spaces is said to be '' orientable''.See also
* * * * * * * *References
External links
* {{DEFAULTSORT:Orientation (vector space) Linear algebra Analytic geometry Orientation (geometry)