moment (physics) on:
[Wikipedia]
[Google]
[Amazon]
In
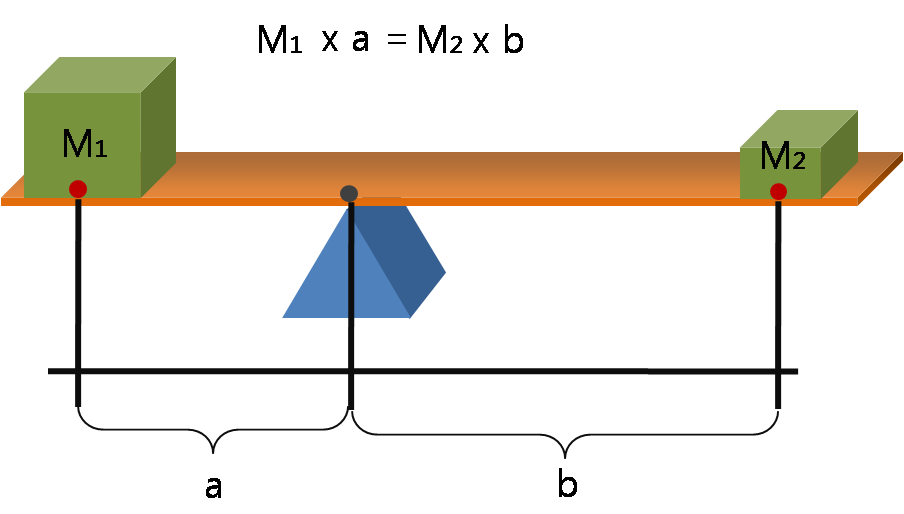 In works believed to stem from
In works believed to stem from
An English translation
appears in 1842. In 1884, the term ''
A dictionary definition of moment. Length Physical quantities el:Ροπή sq:Momenti
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which rel ...
, a moment is a mathematical expression involving the product of a distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...
and physical quantity
A physical quantity is a physical property of a material or system that can be quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ' Numerical value ' and a ' Unit '. For examp ...
. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. In this way, the moment accounts for the quantity's location or arrangement. For example, the moment of force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a ...
, often called torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of t ...
, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different element ...
es, and electric charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respecti ...
distributions.
Elaboration
In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : where is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity is not concentrated solely at a single point, the moment is theintegral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
of that quantity's density over space:
:
where is the distribution of the density of charge, mass, or whatever quantity is being considered.
More complex forms take into account the angular relationships between the distance and the physical quantity, but the above equations capture the essential feature of a moment, namely the existence of an underlying or equivalent term. This implies that there are multiple moments (one for each value of ''n'') and that the moment generally depends on the reference point from which the distance is measured, although for certain moments (technically, the lowest non-zero moment) this dependence vanishes and the moment becomes independent of the reference point.
Each value of ''n'' corresponds to a different moment: the 1st moment corresponds to ''n'' = 1; the 2nd moment to ''n'' = 2, etc. The 0th moment (''n'' = 0) is sometimes called the ''monopole moment''; the 1st moment (''n'' = 1) is sometimes called the ''dipole moment'', and the 2nd moment (''n'' = 2) is sometimes called the '' quadrupole moment'', especially in the context of electric charge distributions.
Examples
* The ''moment of force'', or ''torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of t ...
'', is a first moment: , or, more generally, .
* Similarly, ''angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed sy ...
'' is the 1st moment of momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass ...
: . Note that momentum itself is ''not'' a moment.
* The '' electric dipole moment'' is also a 1st moment: for two opposite point charges or for a distributed charge with charge density .
Moments of mass:
* The ''total mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different element ...
'' is the zeroth moment of mass.
* The '' center of mass'' is the 1st moment of mass normalized by total mass: for a collection of point masses, or for an object with mass distribution .
* The '' moment of inertia'' is the 2nd moment of mass: for a point mass, for a collection of point masses, or for an object with mass distribution . Note that the center of mass is often (but not always) taken as the reference point.
Multipole moments
Assuming a density function that is finite and localized to a particular region, outside that region a 1/''r'' potential may be expressed as a series of spherical harmonics: : The coefficients are known as ''multipole moments'', and take the form: : where expressed in spherical coordinates is a variable of integration. A more complete treatment may be found in pages describing multipole expansion or spherical multipole moments. (Note: the convention in the above equations was taken from Jackson – the conventions used in the referenced pages may be slightly different.) When represents an electric charge density, the are, in a sense, projections of the moments of electric charge: is the monopole moment; the are projections of the dipole moment, the are projections of the quadrupole moment, etc.Applications of multipole moments
The multipole expansion applies to 1/''r'' scalar potentials, examples of which include theelectric potential
The electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in ...
and the gravitational potential. For these potentials, the expression can be used to approximate the strength of a field produced by a localized distribution of charges (or mass) by calculating the first few moments. For sufficiently large ''r'', a reasonable approximation can be obtained from just the monopole and dipole moments. Higher fidelity can be achieved by calculating higher order moments. Extensions of the technique can be used to calculate interaction energies and intermolecular forces.
The technique can also be used to determine the properties of an unknown distribution . Measurements pertaining to multipole moments may be taken and used to infer properties of the underlying distribution. This technique applies to small objects such as molecules,
but has also been applied to the universe itself, being for example the technique employed by the WMAP and Planck experiments to analyze the cosmic microwave background
In Big Bang cosmology the cosmic microwave background (CMB, CMBR) is electromagnetic radiation that is a remnant from an early stage of the universe, also known as "relic radiation". The CMB is faint cosmic background radiation filling all spac ...
radiation.
History
 In works believed to stem from
In works believed to stem from Ancient Greece
Ancient Greece ( el, Ἑλλάς, Hellás) was a northeastern Mediterranean civilization, existing from the Greek Dark Ages of the 12th–9th centuries BC to the end of classical antiquity ( AD 600), that comprised a loose collection of cult ...
, the concept of a moment is alluded to by the word ῥοπή (''rhopḗ'', "inclination") and composites like ἰσόρροπα (''isorropa'', "of equal inclinations"). The context of these works is mechanics
Mechanics (from Ancient Greek: μηχανική, ''mēkhanikḗ'', "of machines") is the area of mathematics and physics concerned with the relationships between force, matter, and motion among physical objects. Forces applied to objects ...
and geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
involving the lever. In particular, in extant works attributed to Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scienti ...
, the moment is pointed out in phrasings like:
:"Commensurable
Two concepts or things are commensurable if they are measurable or comparable by a common standard.
Commensurability most commonly refers to commensurability (mathematics). It may also refer to:
* Commensurability (astronomy), whether two orbit ...
magnitudes ( ) and Bare equally balanced () if their distances o the center Γ, i.e., ΑΓ and ΓΒare inversely proportional () to their weights ()."
Moreover, in extant texts such as '' The Method of Mechanical Theorems'', moments are used to infer the center of gravity, area, and volume of geometric figures.
In 1269, William of Moerbeke
William of Moerbeke, O.P. ( nl, Willem van Moerbeke; la, Guillelmus de Morbeka; 1215–35 – 1286), was a prolific medieval translator of philosophical, medical, and scientific texts from Greek language into Latin, enabled by the period ...
translates various works of Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scienti ...
and Eutocious into Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power ...
. The term ῥοπή is transliterated
Transliteration is a type of conversion of a text from one script to another that involves swapping letters (thus ''trans-'' + '' liter-'') in predictable ways, such as Greek → , Cyrillic → , Greek → the digraph , Armenian → or ...
into ''ropen''.
Around 1450, Jacobus Cremonensis translates ῥοπή in similar texts into the Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power ...
term ''momentum'' ( "movement"). The same term is kept in a 1501 translation by Giorgio Valla, and subsequently by Francesco Maurolico, Federico Commandino, Guidobaldo del Monte, Adriaan van Roomen, Florence Rivault, Francesco Buonamici, Marin Mersenne, and Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He w ...
. That said, why was the word ''momentum'' chosen for the translation? One clue, according to Treccani, is that ''momento'' in Medieval Italy, the place the early translators lived, in a transferred sense meant both a "moment of time" and a "moment of weight" (a small amount of weight that turns the scale
Scale or scales may refer to:
Mathematics
* Scale (descriptive set theory), an object defined on a set of points
* Scale (ratio), the ratio of a linear dimension of a model to the corresponding dimension of the original
* Scale factor, a number ...
).
In 1554, Francesco Maurolico clarifies the Latin term ''momentum'' in the work ''Prologi sive sermones''. Here is a Latin to English translation as given by Marshall Clagett:
" ..equal weights at unequal distances do not weigh equally, but unequal weightsin 1586, Simon Stevin uses the Dutch term ''staltwicht'' ("parked weight") for momentum in '' De Beghinselen Der Weeghconst''. In 1632,t these unequal distances may T, or t, is the twentieth letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''tee'' (pronounced ), plural ''tees''. It is de ...weigh equally. For a weight suspended at a greater distance is heavier, as is obvious in a balance. Therefore, there exists a certain third kind of power or third difference of magnitude—one that differs from both body and weight—and this they call moment. Therefore, a body acquires weight from both quantity .e., sizeand quality .e., material but a weight receives its moment from the distance at which it is suspended. Therefore, when distances are reciprocally proportional to weights, the momentsf the weights F, or f, is the sixth letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''ef'' (pronounced ), and the plural is ''efs''. Hist ...are equal, asArchimedes Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scienti ...demonstrated in '' The Book on Equal Moments''. Therefore, weights or athermoments like other continuous quantities, are joined at some common terminus, that is, at something common to both of them like the center of weight, or at a point of equilibrium. Now the center of gravity in any weight is that point which, no matter how often or whenever the body is suspended, always inclines perpendicularly toward the universal center. In addition to body, weight, and moment, there is a certain fourth power, which can be called impetus or force.Aristotle Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical Greece, Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatet ...investigates it in ''On Mechanical Questions'', and it is completely different from hethree aforesaid owers or magnitudes ..
Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He w ...
publishes '' Dialogue Concerning the Two Chief World Systems'' and uses the Italian ''momento'' with many meanings, including the one of his predecessors.
In 1643, Thomas Salusbury translates some of Galilei's works into English. Salusbury translates Latin ''momentum'' and Italian ''momento'' into the English term ''moment''.
In 1765, the Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power ...
term ''momentum inertiae'' ( English: '' moment of inertia'') is used by Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
to refer to one of Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists ...
's quantities in '' Horologium Oscillatorium''. From page 166: ''"Definitio 7. 422. Momentum inertiae corporis respectu eujuspiam axis est summa omnium productorum, quae oriuntur, si singula corporis elementa per quadrata distantiarum suarum ab axe multiplicentur."'' (Definition 7. 422. A body's moment of inertia with respect to any axis is the sum of all of the products, which arise, if the individual elements of the body are multiplied by the square of their distances from the axis.) Huygens 1673 work involving finding the center of oscillation had been stimulated by Marin Mersenne, who suggested it to him in 1646.
In 1811, the French term ''moment d'une force'' ( English: ''moment of force'') with respect to a point and plane is used by Siméon Denis Poisson
Baron Siméon Denis Poisson FRS FRSE (; 21 June 1781 – 25 April 1840) was a French mathematician and physicist who worked on statistics, complex analysis, partial differential equations, the calculus of variations, analytical mechanics, electr ...
in ''Traité de mécanique''An English translation
appears in 1842. In 1884, the term ''
torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of t ...
'' is suggested by James Thomson in the context of measuring rotational forces of machines (with propeller
A propeller (colloquially often called a screw if on a ship or an airscrew if on an aircraft) is a device with a rotating hub and radiating blades that are set at a pitch to form a helical spiral which, when rotated, exerts linear thrust upon ...
s and rotors). Today, a dynamometer is used to measure the torque of machines.
In 1893, Karl Pearson uses the term ''n-th moment'' and in the context of curve-fitting scientific measurements. Pearson wrote in response to John Venn, who, some years earlier, observed a peculiar pattern involving meteorological data and asked for an explanation of its cause. In Pearson's response, this analogy is used: the mechanical "center of gravity" is the mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set.
For a data set, the '' ari ...
and the "distance" is the deviation from the mean. This later evolved into moments in mathematics. The analogy between the mechanical concept of a moment and the statistical function involving the sum of the th powers of deviations was noticed by several earlier, including Laplace, Kramp Kramp is a surname. Notable people with the surname include:
*Christian Kramp (1760–1826), French mathematician who worked primarily with factorials
*Daryl Kramp
Daryl Kramp (born June 14, 1947) is a Canadian politician. He served as the Conse ...
, Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
, Encke, Czuber, Quetelet, and De Forest.
See also
*Torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of t ...
(or ''moment of force''), see also the article couple (mechanics)
* Moment (mathematics)
* Mechanical equilibrium, applies when an object is balanced so that the sum of the clockwise moments about a pivot is equal to the sum of the anticlockwise moments about the same pivot
* Moment of inertia , analogous to mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different element ...
in discussions of rotational motion. It is a measure of an object's resistance to changes in its rotation rate
* Moment of momentum , the rotational analog of linear momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass ...
.
* Magnetic moment , a dipole moment measuring the strength and direction of a magnetic source.
* Electric dipole moment, a dipole moment measuring the charge difference and direction between two or more charges. For example, the electric dipole moment between a charge of –''q'' and ''q'' separated by a distance of d is
* Bending moment, a moment that results in the bending of a structural element
* First moment of area, a property of an object related to its resistance to shear stress
* Second moment of area, a property of an object related to its resistance to bending and deflection
* Polar moment of inertia, a property of an object related to its resistance to torsion
* Image moments, statistical properties of an image
* Seismic moment, quantity used to measure the size of an earthquake
* Plasma moments, fluid description of plasma in terms of density, velocity and pressure
* List of area moments of inertia
* List of moments of inertia
* Multipole expansion
* Spherical multipole moments
Notes
References
External links
*{{Commonscatinline, Moment (physics)A dictionary definition of moment. Length Physical quantities el:Ροπή sq:Momenti