
A hierarchy (from
Greek: , from , 'president of sacred rites') is an arrangement of items (objects, names, values, categories, etc.) that are represented as being "above", "below", or "at the same level as" one another. Hierarchy is an important concept in a wide variety of fields, such as
architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and construction, constructi ...
,
philosophy
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational an ...
,
design
A design is the concept or proposal for an object, process, or system. The word ''design'' refers to something that is or has been intentionally created by a thinking agent, and is sometimes used to refer to the inherent nature of something ...
,
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
,
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
,
organizational theory,
systems theory,
systematic biology, and the
social sciences
Social science (often rendered in the plural as the social sciences) is one of the branches of science, devoted to the study of society, societies and the Social relation, relationships among members within those societies. The term was former ...
(especially
political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, polit ...
).
A hierarchy can link entities either directly or indirectly, and either vertically or diagonally. The only direct links in a hierarchy, insofar as they are hierarchical, are to one's immediate superior or to one of one's
subordinates, although a system that is largely hierarchical can also incorporate alternative hierarchies. Hierarchical links can extend "vertically" upwards or downwards via multiple links in the same direction, following a
path. All parts of the hierarchy that are not linked vertically to one another nevertheless can be "horizontally" linked through a path by traveling up the hierarchy to find a common direct or indirect superior, and then down again. This is akin to two
co-workers or
colleagues; each reports to a common superior, but they have the same relative amount of authority. Organizational forms exist that are both alternative and complementary to hierarchy.
Heterarchy is one such form.
Nomenclature
Hierarchies have their own special vocabulary. These terms are easiest to understand when a hierarchy is diagrammed (see
below).
In an organizational context, the following terms are often used related to hierarchies:
[
* Object: one entity (e.g., a person, department or ]concept
A concept is an abstract idea that serves as a foundation for more concrete principles, thoughts, and beliefs.
Concepts play an important role in all aspects of cognition. As such, concepts are studied within such disciplines as linguistics, ...
or element of arrangement or member of a set)
* System
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
: the entire set of objects that are being arranged hierarchically (e.g., an administration)
* Dimension: another word for "system" from on-line analytical processing (e.g. cubes)
* Member: an (element or object) at any (level or rank) in a (class-system, taxonomy or dimension)
*Terms about Positioning
** Rank: the relative value, worth, complexity, power, importance, authority, level etc. of an object
** Level or Tier: a set of objects with the same rank OR importance
** Ordering: the arrangement of the (ranks or levels)
**Hierarchy: the arrangement of a particular set of members into (ranks or levels). Multiple hierarchies are possible per (dimension taxonomy or Classification-system), in which selected levels of the dimension are omitted to flatten the structure
*Terms about Placement
** Hierarch, the apex of the hierarchy, consisting of one single orphan (object or member) in the top level of a dimension. The root of an inverted-tree structure
** Member, a (member or node) in any level of a hierarchy in a dimension to which (superior and subordinate) members are attached
** Orphan, a member in any level of a dimension without a parent member. Often the apex of a disconnected branch. Orphans can be grafted back into the hierarchy by creating a relationship (interaction) with a parent in the immediately superior level
**Leaf
A leaf (: leaves) is a principal appendage of the plant stem, stem of a vascular plant, usually borne laterally above ground and specialized for photosynthesis. Leaves are collectively called foliage, as in "autumn foliage", while the leav ...
, a member in any level of a dimension without subordinates in the hierarchy
** Neighbour: a member adjacent to another member in the same (level or rank). Always a peer.
** Superior: a higher level or an object ranked at a higher level (A parent or an ancestor)
** Subordinate: a lower level or an object ranked at a lower level (A child or a descendant)
** Collection: all of the objects at one level (i.e. Peers)
** Peer: an object with the same rank (and therefore at the same level)
** Interaction: the relationship between an object and its direct superior or subordinate (i.e. a superior/inferior pair)
*** a direct interaction occurs when one object is on a level exactly one higher or one lower than the other (i.e., on a tree, the two objects have a line between them)
** Distance: the minimum number of connections between two objects, i.e., one less than the number of objects that need to be "crossed" to trace a path from one object to another
** Span: a qualitative description of the width of a level when diagrammed, i.e., the number of subordinates an object has
*Terms about Nature
** Attribute: a heritable characteristic of (members and their subordinates) in a level (e.g. ''hair-colour'')
** Attribute-value: the specific value of a heritable characteristic (e.g. ''Auburn'')
In a mathematical context (in graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
), the general terminology used is different.
Most hierarchies use a more specific vocabulary pertaining to their subject, but the idea behind them is the same. For example, with data structure
In computer science, a data structure is a data organization and storage format that is usually chosen for Efficiency, efficient Data access, access to data. More precisely, a data structure is a collection of data values, the relationships amo ...
s, objects are known as nodes, superiors are called parents
A parent is either the progenitor of a child or, in humans, it can refer to a caregiver or legal guardian, generally called an adoptive parent or step-parent. Parents who are progenitors are first-degree relatives and have 50% genetic meet. ...
and subordinates are called children. In a business setting, a superior is a supervisor/boss and a peer is a colleague.
Degree of branching
Degree of branching refers to the number of direct subordinates or children an object has (in graph theory, equivalent to the number of other vertices connected to via outgoing arcs, in a directed graph) a node has. Hierarchies can be categorized based on the "maximum degree", the highest degree present in the system as a whole. Categorization in this way yields two broad classes: ''linear'' and ''branching''.
In a linear hierarchy, the maximum degree is 1.[ In other words, all of the objects can be visualized in a line-up, and each object (excluding the top and bottom ones) has exactly one direct subordinate and one direct superior. This is referring to the ''objects'' and not the ''levels''; every hierarchy has this property with respect to levels, but normally each level can have an infinite number of objects.
In a branching hierarchy, one or more objects has a degree of 2 or more (and therefore the minimum degree is 2 or higher).][ For many people, the word "hierarchy" automatically evokes an image of a branching hierarchy.][ Branching hierarchies are present within numerous systems, including ]organization
An organization or organisation (English in the Commonwealth of Nations, Commonwealth English; American and British English spelling differences#-ise, -ize (-isation, -ization), see spelling differences) is an legal entity, entity—such as ...
s and classification schemes. The broad category of branching hierarchies can be further subdivided based on the degree.
A flat hierarchy (also known for companies as flat organization) is a branching hierarchy in which the maximum degree approaches infinity, i.e., that has a wide span.diamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of e ...
s and graphite are flat hierarchies of numerous carbon
Carbon () is a chemical element; it has chemical symbol, symbol C and atomic number 6. It is nonmetallic and tetravalence, tetravalent—meaning that its atoms are able to form up to four covalent bonds due to its valence shell exhibiting 4 ...
atoms that can be further decomposed into subatomic particles.
An overlapping hierarchy is a branching hierarchy in which at least one object has two parent objects.[ For example, a graduate student can have two co-supervisors to whom the student reports directly and equally, and who have the same level of authority within the ]university
A university () is an educational institution, institution of tertiary education and research which awards academic degrees in several Discipline (academia), academic disciplines. ''University'' is derived from the Latin phrase , which roughly ...
hierarchy (i.e., they have the same position or tenure status).
Etymology
Possibly the first use of the English word ''hierarchy'' cited by the ''Oxford English Dictionary
The ''Oxford English Dictionary'' (''OED'') is the principal historical dictionary of the English language, published by Oxford University Press (OUP), a University of Oxford publishing house. The dictionary, which published its first editio ...
'' was in 1881, when it was used in reference to the three orders of three angels as depicted by Pseudo-Dionysius the Areopagite (5th–6th centuries). Pseudo-Dionysius used the related Greek word (ἱεραρχία, ) both in reference to the celestial hierarchy and the ecclesiastical hierarchy. The Greek term ''hierarchia'' means 'rule of a high priest', from (ἱεράρχης, 'president of sacred rites, high-priest') and that from ''hiereus'' (ἱερεύς, 'priest') and ''arche'' (ἀρχή, 'first place or power, rule'). Dionysius is credited with first use of it as an abstract noun.
Since hierarchical churches, such as the Roman Catholic
The Catholic Church (), also known as the Roman Catholic Church, is the largest Christian church, with 1.27 to 1.41 billion baptized Catholics worldwide as of 2025. It is among the world's oldest and largest international institut ...
(see Catholic Church hierarchy) and Eastern Orthodox
Eastern Orthodoxy, otherwise known as Eastern Orthodox Christianity or Byzantine Christianity, is one of the three main Branches of Christianity, branches of Chalcedonian Christianity, alongside Catholic Church, Catholicism and Protestantism ...
churches, had tables of organization that were "hierarchical" in the modern sense of the word (traditionally with God
In monotheistic belief systems, God is usually viewed as the supreme being, creator, and principal object of faith. In polytheistic belief systems, a god is "a spirit or being believed to have created, or for controlling some part of the un ...
as the pinnacle or head of the hierarchy), the term came to refer to similar organizational methods in secular settings.
Representing hierarchies
A hierarchy is typically depicted as a pyramid, where the height of a level represents that level's status and width of a level represents the quantity of items at that level relative to the whole. For example, the few Directors of a company could be at the apex, and the base could be thousands of people who have no subordinates.
These pyramids are often diagrammed with a triangle diagram which serves to emphasize the size differences between the levels (but not all triangle/pyramid diagrams are hierarchical; for example, the 1992 USDA food guide pyramid). An example of a triangle diagram appears to the right.
Another common representation of a hierarchical scheme is as a tree diagram. Phylogenetic trees, charts showing the structure of , and playoff brackets in sports are often illustrated this way.
More recently, as computers have allowed the storage and navigation of ever larger data sets, various methods have been developed to represent hierarchies in a manner that makes more efficient use of the available space on a computer's screen. Examples include fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
maps, TreeMaps and Radial Trees.
Visual hierarchy
In the design field, mainly graphic design, successful layouts and formatting of the content on documents are heavily dependent on the rules of visual hierarchy. Visual hierarchy is also important for proper organization of files on computers.
An example of visually representing hierarchy is through nested clusters. Nested clusters represent hierarchical relationships using layers of information. The child element is within the parent element, such as in a Venn diagram. This structure is most effective in representing simple hierarchical relationships. For example, when directing someone to open a file on a computer desktop, one may first direct them towards the main folder, then the subfolders within the main folder. They will keep opening files within the folders until the designated file is located.
For more complicated hierarchies, the stair structure represents hierarchical relationships through the use of visual stacking. Visually imagine the top of a downward staircase beginning at the left and descending on the right. Child elements are towards the bottom of the stairs and parent elements are at the top. This structure represents hierarchical relationships through the use of visual stacking.
Informal representation
In plain English, a hierarchy can be thought of as a set in which:
Mathematical representation
Mathematically, in its most general form, a hierarchy is a partially ordered set or ''poset''.system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
in this case is the entire poset, which is constituted of elements. Within this system, each element shares a particular unambiguous property. Objects with the same property value are grouped together, and each of those resulting levels is referred to as a class.
"Hierarchy" is particularly used to refer to a poset in which the classes are organized in terms of increasing complexity.
Operations such as addition, subtraction, multiplication and division are often performed in a certain sequence or order. Usually, addition and subtraction are performed after multiplication and division has already been applied to a problem. The use of parentheses is also a representation of hierarchy, for they show which operation is to be done prior to the following ones. For example:
(2 + 5) × (7 - 4).
In this problem, typically one would multiply 5 by 7 first, based on the rules of mathematical hierarchy. But when the parentheses are placed, one will know to do the operations within the parentheses first before continuing on with the problem. These rules are largely dominant in algebraic problems, ones that include several steps to solve. The use of hierarchy in mathematics is beneficial to quickly and efficiently solve a problem without having to go through the process of slowly dissecting the problem. Most of these rules are now known as the proper way into solving certain equations.
Subtypes
Nested hierarchy
 A nested hierarchy or ''inclusion hierarchy'' is a hierarchical ordering of nested sets.
A nested hierarchy or ''inclusion hierarchy'' is a hierarchical ordering of nested sets.Linnaean taxonomy
Linnaean taxonomy can mean either of two related concepts:
# The particular form of biological classification (taxonomy) set up by Carl Linnaeus, as set forth in his ''Systema Naturae'' (1735) and subsequent works. In the taxonomy of Linnaeus th ...
(the version he laid out in the 10th edition of ''Systema Naturae
' (originally in Latin written ' with the Orthographic ligature, ligature æ) is one of the major works of the Sweden, Swedish botanist, zoologist and physician Carl Linnaeus (1707–1778) and introduced the Linnaean taxonomy. Although the syste ...
''), a human can be formulated as:
:
Taxonomies may change frequently (as seen in biological taxonomy), but the underlying concept of nested hierarchies is always the same.
In many programming taxonomies and syntax models (as well as fractals in mathematics), nested hierarchies, including Russian dolls, are also used to illustrate the properties of self-similarity and recursion
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in m ...
. Recursion itself is included as a subset of hierarchical programming, and recursive thinking can be synonymous with a form of hierarchical thinking and logic.
Containment hierarchy
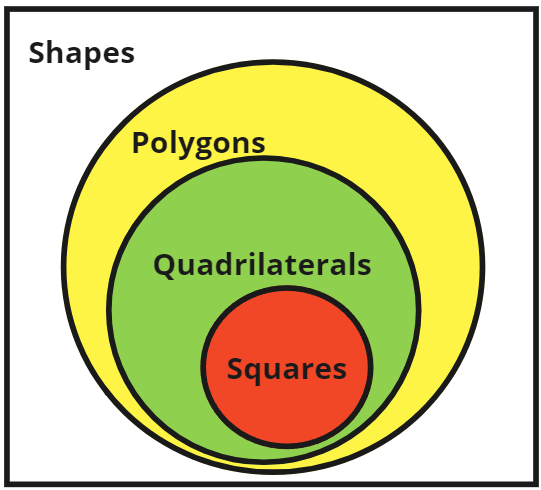 A containment hierarchy is a direct extrapolation of the nested hierarchy concept. All of the ordered sets are still nested, but every set must be " strict"—no two sets can be identical. The shapes example above can be modified to demonstrate this:
:
The notation means ''x'' is a subset of ''y'' but is not equal to ''y''.
A general example of a containment hierarchy is demonstrated in class inheritance in
A containment hierarchy is a direct extrapolation of the nested hierarchy concept. All of the ordered sets are still nested, but every set must be " strict"—no two sets can be identical. The shapes example above can be modified to demonstrate this:
:
The notation means ''x'' is a subset of ''y'' but is not equal to ''y''.
A general example of a containment hierarchy is demonstrated in class inheritance in object-oriented programming
Object-oriented programming (OOP) is a programming paradigm based on the concept of '' objects''. Objects can contain data (called fields, attributes or properties) and have actions they can perform (called procedures or methods and impl ...
.
Two types of containment hierarchies are the ''subsumptive'' containment hierarchy and the ''compositional'' containment hierarchy. A subsumptive hierarchy " subsumes" its children, and a compositional hierarchy is " composed" of its children. A hierarchy can also be both subsumptive ''and'' compositional.
Subsumptive containment hierarchy
A '' subsumptive'' containment hierarchy is a classification of object classes from the general to the specific. Other names for this type of hierarchy are "taxonomic hierarchy" and " IS-A hierarchy".concept
A concept is an abstract idea that serves as a foundation for more concrete principles, thoughts, and beliefs.
Concepts play an important role in all aspects of cognition. As such, concepts are studied within such disciplines as linguistics, ...
s".[ For example, with the Linnaean hierarchy outlined above, an entity name like ''Animalia'' is a way to group all the species that fit the conceptualization of an animal.
]
Compositional containment hierarchy
A ''compositional'' containment hierarchy is an ordering of the parts that make up a system—the system is "composed" of these parts.molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemi ...
s, which are composed of atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
s. In fact, the last two levels apply to all matter, at least at the macroscopic scale. Moreover, each of these levels inherit all the properties of their children.
In this particular example, there are also '' emergent properties''—functions that are not seen at the lower level (e.g., cognition
Cognition is the "mental action or process of acquiring knowledge and understanding through thought, experience, and the senses". It encompasses all aspects of intellectual functions and processes such as: perception, attention, thought, ...
is not a property of neurons but is of the brain
The brain is an organ (biology), organ that serves as the center of the nervous system in all vertebrate and most invertebrate animals. It consists of nervous tissue and is typically located in the head (cephalization), usually near organs for ...
)—and a scalar quality (molecules are bigger than atoms, cells are bigger than molecules, etc.). Both of these concepts commonly exist in compositional hierarchies, but they are not a required general property. These ''level hierarchies'' are characterized by bi-directional causation.[ ''Upward causation'' involves lower-level entities causing some property of a higher level entity; children entities may interact to yield parent entities, and parents are composed at least partly by their children. '' Downward causation'' refers to the effect that the incorporation of entity ''x'' into a higher-level entity can have on ''xs properties and interactions. Furthermore, the entities found at each level are '' autonomous''.
]
Contexts and applications
Kulish (2002) suggests that almost every system of organization which humans apply to the world is arranged hierarchically.nation
A nation is a type of social organization where a collective Identity (social science), identity, a national identity, has emerged from a combination of shared features across a given population, such as language, history, ethnicity, culture, t ...
has a government and that every government is hierarchical. Sociologists can analyse socioeconomic systems in terms of stratification into a social hierarchy (the social stratification of societies), and all systematic classification schemes ( taxonomies) are hierarchical. Most organized religions, regardless of their internal governance structures, operate as a hierarchy under deities
A deity or god is a supernatural being considered to be sacred and worthy of worship due to having authority over some aspect of the universe and/or life. The ''Oxford Dictionary of English'' defines ''deity'' as a God (male deity), god or god ...
and priesthoods. Many Christian denominations have an autocephalous ecclesiastical hierarchy of leadership
Leadership, is defined as the ability of an individual, group, or organization to "", influence, or guide other individuals, teams, or organizations.
"Leadership" is a contested term. Specialist literature debates various viewpoints on the co ...
. Families can be viewed as hierarchical structures in terms of cousinship (e.g., first cousin once removed, second cousin, etc.), ancestry (as depicted in a family tree) and inheritance
Inheritance is the practice of receiving private property, titles, debts, entitlements, privileges, rights, and obligations upon the death of an individual. The rules of inheritance differ among societies and have changed over time. Offi ...
( succession and heir
Inheritance is the practice of receiving private property, titles, debts, entitlements, privileges, rights, and obligations upon the death of an individual. The rules of inheritance differ among societies and have changed over time. Offi ...
ship). All the requisites of a well-rounded life and lifestyle can be organized using Maslow's hierarchy of human needs - according to Maslow's hierarchy of human needs. Learning
Learning is the process of acquiring new understanding, knowledge, behaviors, skills, value (personal and cultural), values, Attitude (psychology), attitudes, and preferences. The ability to learn is possessed by humans, non-human animals, and ...
steps often follow a hierarchical scheme—to master differential equations one must first learn calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
; to learn calculus one must first learn elementary algebra; and so on. Nature
Nature is an inherent character or constitution, particularly of the Ecosphere (planetary), ecosphere or the universe as a whole. In this general sense nature refers to the Scientific law, laws, elements and phenomenon, phenomena of the physic ...
offers hierarchical structures, as numerous schemes such as Linnaean taxonomy
Linnaean taxonomy can mean either of two related concepts:
# The particular form of biological classification (taxonomy) set up by Carl Linnaeus, as set forth in his ''Systema Naturae'' (1735) and subsequent works. In the taxonomy of Linnaeus th ...
, the organization of life, and biomass pyramids attempt to document.
While the above examples are often clearly depicted in a hierarchical form and are classic examples, hierarchies exist in numerous systems where this branching structure is not immediately apparent. For example, most postal-code systems are hierarchical. Using the Canadian postal code system as an example, the top level's binding concept, the "postal district", consists of 18 objects (letters). The next level down is the "zone", where the objects are the digits 0–9. This is an example of an overlapping hierarchy, because each of these 10 objects has 18 parents. The hierarchy continues downward to generate, in theory, 7,200,000 unique codes of the format ''A0A 0A0'' (the second and third letter positions allow 20 objects each). Most library classification systems are also hierarchical. The Dewey Decimal System is infinitely hierarchical because there is no finite bound on the number of digits can be used after the decimal point.
Organizations
Organization
An organization or organisation (English in the Commonwealth of Nations, Commonwealth English; American and British English spelling differences#-ise, -ize (-isation, -ization), see spelling differences) is an legal entity, entity—such as ...
s can be structured as a dominance hierarchy. In an organizational hierarchy, there is a single person or group with the most power or authority, and each subsequent level represents a lesser authority. Most organizations are structured in this manner, including governments, companies, armed forces
A military, also known collectively as armed forces, is a heavily armed, highly organized force primarily intended for warfare. Militaries are typically authorized and maintained by a sovereign state, with their members identifiable by a ...
, militia and organized religions. The units or persons within an organization may be depicted hierarchically in an organizational chart.
In a reverse hierarchy, the conceptual pyramid of authority is turned upside-down, so that the apex is at the bottom and the base is at the top. This mode represents the idea that members of the higher rankings are responsible for the members of the lower rankings.
Biology
Empirically, when we observe in nature a large proportion of the (complex) biological systems, they exhibit hierarchic structure. On theoretical grounds we could expect complex systems to be hierarchies in a world in which complexity had to evolve from simplicity. System
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
hierarchies analysis performed in the 1950s, laid the empirical foundations for a field that would become, from the 1980s, hierarchical ecology.
The theoretical foundations are summarized by thermodynamics
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed b ...
.
When biological systems are modeled as physical system
A physical system is a collection of physical objects under study. The collection differs from a set: all the objects must coexist and have some physical relationship.
In other words, it is a portion of the physical universe chosen for analys ...
s, in the most general abstraction, they are thermodynamic open systems that exhibit self-organised behavior, and the set/subset relations between dissipative structures can be characterized in a hierarchy.
Other hierarchical representations related to biology include ecological pyramids which illustrate energy flow or trophic levels in ecosystems, and taxonomic hierarchies, including the Linnean classification scheme and phylogenetic trees that reflect inferred patterns of evolutionary relationship among living and extinct species.
Computer-graphic imaging
CGI and computer-animation programs mostly use hierarchies for models. On a 3D model of a human
Humans (''Homo sapiens'') or modern humans are the most common and widespread species of primate, and the last surviving species of the genus ''Homo''. They are Hominidae, great apes characterized by their Prehistory of nakedness and clothing ...
for example, the chest is a parent
A parent is either the progenitor of a child or, in humans, it can refer to a caregiver or legal guardian, generally called an adoptive parent or step-parent. Parents who are progenitors are First-degree relative, first-degree relatives and have ...
of the upper left arm, which is a parent of the lower left arm, which is a parent of the hand
A hand is a prehensile, multi-fingered appendage located at the end of the forearm or forelimb of primates such as humans, chimpanzees, monkeys, and lemurs. A few other vertebrates such as the Koala#Characteristics, koala (which has two thumb#O ...
. This pattern is used in modeling and animation for almost everything built as a 3D digital model.
Linguistics
Many grammatical theories, such as phrase-structure grammar, involve hierarchy.
Direct–inverse languages such as Cree and Mapudungun distinguish subject and object on verb
A verb is a word that generally conveys an action (''bring'', ''read'', ''walk'', ''run'', ''learn''), an occurrence (''happen'', ''become''), or a state of being (''be'', ''exist'', ''stand''). In the usual description of English, the basic f ...
s not by different subject and object markers, but via a hierarchy of persons.
In this system, the three (or four with Algonquian languages) persons occur in a hierarchy of salience. To distinguish which is subject and which object, ''inverse markers'' are used if the object outranks the subject.
On the other hand, languages include a variety of phenomena that are not hierarchical. For example, the relationship between a pronoun and a prior noun-phrase to which it refers commonly crosses grammatical boundaries in non-hierarchical ways.
Music
The structure of a musical composition is often understood hierarchically (for example by Heinrich Schenker (1768–1835, see Schenkerian analysis), and in the (1985) Generative Theory of Tonal Music, by composer Fred Lerdahl and linguist Ray Jackendoff). The sum of all notes in a piece is understood to be an all-inclusive surface, which can be reduced to successively more sparse and more fundamental types of motion. The levels of structure that operate in Schenker's theory are the foreground, which is seen in all the details of the musical score; the middle ground, which is roughly a summary of an essential contrapuntal progression and voice-leading; and the background or Ursatz, which is one of only a few basic "long-range counterpoint" structures that are shared in the gamut of tonal music literature.
The pitches and form of tonal music are organized hierarchically, all pitches deriving their importance from their relationship to a tonic key, and secondary themes in other keys are brought back to the tonic in a recapitulation of the primary theme.
Examples of other applications
Information-based
* Library classification
** Dewey Decimal Classification
City planning-based
* Green transport hierarchy
* Roads
** Streets
* Settlement hierarchy
** As of 2010
** As of 2100 (estimate according to Doxiadis, 1968)
Linguistics-oriented
* Language family tree
* Levels of adequacy for evaluating grammars
* Direct–inverse languages
* Structural linguistics
** Parse tree
** Formal grammars
** Abstract syntax tree
* Evolution of basic color terminology in languages
Power- or authority-based
* Aristocratic hierarchies
** In Europe
Europe is a continent located entirely in the Northern Hemisphere and mostly in the Eastern Hemisphere. It is bordered by the Arctic Ocean to the north, the Atlantic Ocean to the west, the Mediterranean Sea to the south, and Asia to the east ...
** In China
China, officially the People's Republic of China (PRC), is a country in East Asia. With population of China, a population exceeding 1.4 billion, it is the list of countries by population (United Nations), second-most populous country after ...
* Ecclesiastical hierarchies
** Catholic Church hierarchy
** LDS Church hierarchy
** Kimbanguist Church hierarchy
** Raëlism Church hierarchy
** see also autocephaly
* Prussian three-class franchise
* Political party hierarchies
** Nazi Party (''pace'' overlapping fields[
Compare:
])
*** SS
*** Hierarchy of subdivisions within the Gau
** Communist Party of the Soviet Union
** Chinese Communist Party
* Chain of command
** Military ranks
** Military units
** U.S. Military Combatant Commands
* Intraspecial dominance
** Pecking order
* Social classes
** Caste system in India
** Hierarchical structure of Feudal Japan
** White racist hierarchy
** Hierarchy of Exclusion (Ender's Game)
Value-related
* Hierarchy of genres in art
* Evidence
Evidence for a proposition is what supports the proposition. It is usually understood as an indication that the proposition is truth, true. The exact definition and role of evidence vary across different fields. In epistemology, evidence is what J ...
* Human needs
* Precious substances
* Judicial hierarchy of social values
Perception-based
* Color wheel
** Primary colors
*** Secondary colors
**** Tertiary colors
History-oriented
* Three-age system
* Cyclic theory of civilization
** Oswald Spengler
** Arnold J. Toynbee
* Spiral dynamics
Science-focussed
* Hierarchy of organization within the Universe
* Star systems
* Biological classification
In biology, taxonomy () is the scientific study of naming, defining ( circumscribing) and classifying groups of biological organisms based on shared characteristics. Organisms are grouped into taxa (singular: taxon), and these groups are give ...
* Biological organization
* Phylogenetic tree
* Evolutionary development
* Hierarchy of ecological georegions
Technology-based
* Memory hierarchy
** Cache hierarchy
* Clusters
* Class constructs
* Data organization
** Hierarchical query
* Data storage
** Computer files
* Devices
* IP addresses
* Memory
Memory is the faculty of the mind by which data or information is encoded, stored, and retrieved when needed. It is the retention of information over time for the purpose of influencing future action. If past events could not be remembe ...
** Virtual memory allocation
* Networks
* Radio cells
* States (configurations)
* Web addresses
* Structure
** Data Structure
In computer science, a data structure is a data organization and storage format that is usually chosen for Efficiency, efficient Data access, access to data. More precisely, a data structure is a collection of data values, the relationships amo ...
* Inheritance (object-oriented programming)
Religion-related
* Levels of consciousness
** Chakras
** Great chain of being
** G.I. Gurdjieff
** Timothy Leary
* Levels of spiritual development
** In Theravada Buddhism
** In Mahayana Buddhism
* Ages in the evolution of society
** In Astrology
Astrology is a range of Divination, divinatory practices, recognized as pseudoscientific since the 18th century, that propose that information about human affairs and terrestrial events may be discerned by studying the apparent positions ...
** In Hellenism (the Ancient Greek Religion)
** Dispensations in Protestantism
** Dispensations in Mormonism
* Degrees of communion between various Christian churches
* UFO religions
** Command hierarchy of the ''Ashtar Galactic Command'' flying saucer fleet
* Deities
** In Japanese Buddhism
** In Theosophy
* Angels
** In Christianity
Christianity is an Abrahamic monotheistic religion, which states that Jesus in Christianity, Jesus is the Son of God (Christianity), Son of God and Resurrection of Jesus, rose from the dead after his Crucifixion of Jesus, crucifixion, whose ...
** In Islam
Islam is an Abrahamic religions, Abrahamic monotheistic religion based on the Quran, and the teachings of Muhammad. Adherents of Islam are called Muslims, who are estimated to number Islam by country, 2 billion worldwide and are the world ...
** In Judaism
Judaism () is an Abrahamic religions, Abrahamic, Monotheism, monotheistic, ethnic religion that comprises the collective spiritual, cultural, and legal traditions of the Jews, Jewish people. Religious Jews regard Judaism as their means of o ...
*** Kabbalistic
** In Zoroastrianism
Zoroastrianism ( ), also called Mazdayasnā () or Beh-dīn (), is an Iranian religions, Iranian religion centred on the Avesta and the teachings of Zoroaster, Zarathushtra Spitama, who is more commonly referred to by the Greek translation, ...
* Devils and Demons
** Devils
** Demons
* Hells
** In Catholicism (Nine Levels of Hell)
** In Buddhism (Sixteen Levels of Hell)
* Religions in society
* (organizational hierarchies are listed under )
Methods using hierarchy
Criticisms
In the work of diverse theorists such as William James (1842 to 1910), Michel Foucault (1926 to 1984) and Hayden White (1928 to 2018), important critiques of hierarchical epistemology
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowle ...
are advanced. James famously asserts in his work Radical Empiricism that clear distinctions of type and category are a constant but unwritten goal of scientific reasoning, so that when they are discovered, success is declared. But if aspects of the world are organized differently, involving inherent and intractable ambiguities, then scientific questions are often considered unresolved.
Feminists, Marxists, anarchists, communists, critical theorists and others, all of whom have multiple interpretations, criticize the hierarchies commonly found within human society, especially in social relationships. Hierarchies are present in all parts of society: in businesses, schools, families, etc. These relationships are often viewed as necessary. Entities that stand in hierarchical arrangements are animals, humans, plants, etc.
Ethics, behavioral psychology, philosophies of identity
 In
In ethics
Ethics is the philosophy, philosophical study of Morality, moral phenomena. Also called moral philosophy, it investigates Normativity, normative questions about what people ought to do or which behavior is morally right. Its main branches inclu ...
, various virtues are enumerated and sometimes organized hierarchically according to certain brands of virtue theory.
In some of these random examples, there is an asymmetry of 'compositional' significance between levels of structure, so that small parts of the whole hierarchical array depend, for their meaning, on their membership in larger parts. There is a hierarchy of activities in human life: productive activity serves or is guided by the moral life; the moral life is guided by practical reason; practical reason (used in moral and political life) serves contemplative reason (whereby we contemplate God). Practical reason sets aside time and resources for contemplative reason.
See also
Structure-related concepts
''(For example, in )''
* Is-a
** Hypernymy (and supertype)
** Hyponymy (and subtype)
* Has-a
** Holonymy
** Meronymy
Footnotes
Works cited
*
*
*
*
*
*
Further reading
*
*
*
*
*
*
*
*
*
** Also includes full copies of:
**
**
External links
*
{{Authority control
Patterns
Structure
Political culture
 A hierarchy (from Greek: , from , 'president of sacred rites') is an arrangement of items (objects, names, values, categories, etc.) that are represented as being "above", "below", or "at the same level as" one another. Hierarchy is an important concept in a wide variety of fields, such as
A hierarchy (from Greek: , from , 'president of sacred rites') is an arrangement of items (objects, names, values, categories, etc.) that are represented as being "above", "below", or "at the same level as" one another. Hierarchy is an important concept in a wide variety of fields, such as  A nested hierarchy or ''inclusion hierarchy'' is a hierarchical ordering of nested sets. The concept of nesting is exemplified in Russian matryoshka dolls. Each doll is encompassed by another doll, all the way to the outer doll. The outer doll holds all of the inner dolls, the next outer doll holds all the remaining inner dolls, and so on. Matryoshkas represent a nested hierarchy where each level contains only one object, i.e., there is only one of each size of doll; a generalized nested hierarchy allows for multiple objects within levels but with each object having only one parent at each level. The general concept is both demonstrated and mathematically formulated in the following example:
:
A square can always also be referred to as a quadrilateral, polygon or shape. In this way, it is a hierarchy. However, consider the set of polygons using this classification. A square can ''only'' be a quadrilateral; it can never be a triangle, hexagon, etc.
Nested hierarchies are the organizational schemes behind taxonomies and systematic classifications. For example, using the original
A nested hierarchy or ''inclusion hierarchy'' is a hierarchical ordering of nested sets. The concept of nesting is exemplified in Russian matryoshka dolls. Each doll is encompassed by another doll, all the way to the outer doll. The outer doll holds all of the inner dolls, the next outer doll holds all the remaining inner dolls, and so on. Matryoshkas represent a nested hierarchy where each level contains only one object, i.e., there is only one of each size of doll; a generalized nested hierarchy allows for multiple objects within levels but with each object having only one parent at each level. The general concept is both demonstrated and mathematically formulated in the following example:
:
A square can always also be referred to as a quadrilateral, polygon or shape. In this way, it is a hierarchy. However, consider the set of polygons using this classification. A square can ''only'' be a quadrilateral; it can never be a triangle, hexagon, etc.
Nested hierarchies are the organizational schemes behind taxonomies and systematic classifications. For example, using the original  A containment hierarchy is a direct extrapolation of the nested hierarchy concept. All of the ordered sets are still nested, but every set must be " strict"—no two sets can be identical. The shapes example above can be modified to demonstrate this:
:
The notation means ''x'' is a subset of ''y'' but is not equal to ''y''.
A general example of a containment hierarchy is demonstrated in class inheritance in
A containment hierarchy is a direct extrapolation of the nested hierarchy concept. All of the ordered sets are still nested, but every set must be " strict"—no two sets can be identical. The shapes example above can be modified to demonstrate this:
:
The notation means ''x'' is a subset of ''y'' but is not equal to ''y''.
A general example of a containment hierarchy is demonstrated in class inheritance in  In
In