Gradient Descent on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, gradient descent (also often called steepest descent) is a
 Gradient descent is based on the observation that if the multi-variable function is defined and differentiable in a neighborhood of a point , then decreases ''fastest'' if one goes from in the direction of the negative
Gradient descent is based on the observation that if the multi-variable function is defined and differentiable in a neighborhood of a point , then decreases ''fastest'' if one goes from in the direction of the negative
 Gradient descent can be used to solve a system of linear equations
:
reformulated as a quadratic minimization problem.
If the system matrix is real symmetric and positive-definite, an objective function is defined as the quadratic function, with minimization of
:
so that
:
For a general real matrix , linear least squares define
:
In traditional linear least squares for real and the
Gradient descent can be used to solve a system of linear equations
:
reformulated as a quadratic minimization problem.
If the system matrix is real symmetric and positive-definite, an objective function is defined as the quadratic function, with minimization of
:
so that
:
For a general real matrix , linear least squares define
:
In traditional linear least squares for real and the
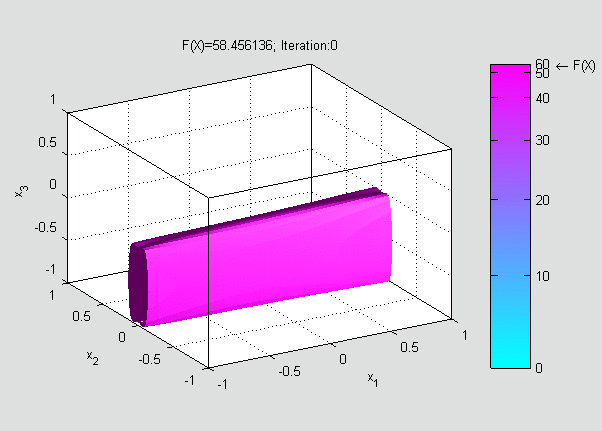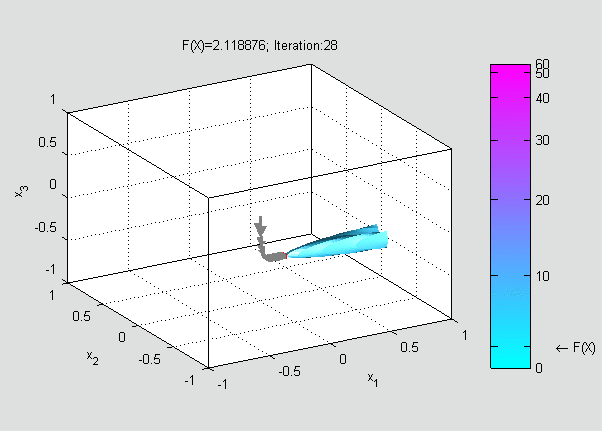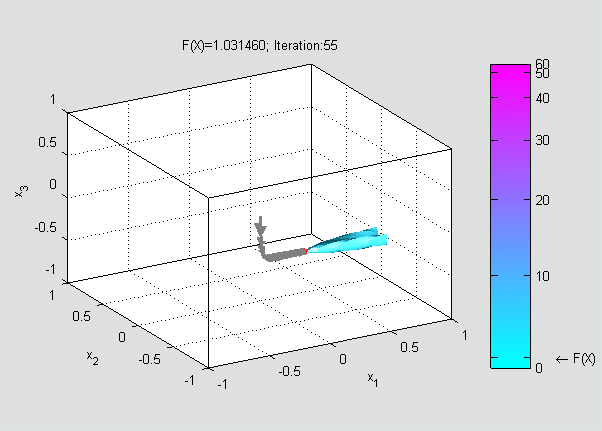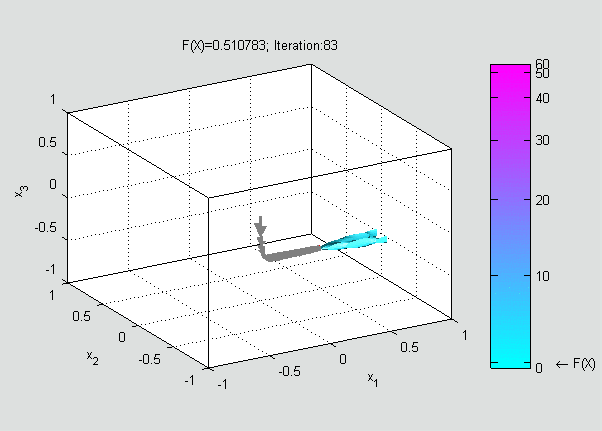 Now, a suitable must be found such that
:
This can be done with any of a variety of line search algorithms. One might also simply guess which gives
:
Evaluating the objective function at this value, yields
:
The decrease from to the next step's value of
:
is a sizable decrease in the objective function. Further steps would reduce its value further until an approximate solution to the system was found.
Now, a suitable must be found such that
:
This can be done with any of a variety of line search algorithms. One might also simply guess which gives
:
Evaluating the objective function at this value, yields
:
The decrease from to the next step's value of
:
is a sizable decrease in the objective function. Further steps would reduce its value further until an approximate solution to the system was found.
Using gradient descent in C++, Boost, Ublas for linear regression
Series of Khan Academy videos discusses gradient ascent
* Archived at ttps://ghostarchive.org/varchive/youtube/20211211/IHZwWFHWa-w Ghostarchiveand th
Wayback Machine
{{DEFAULTSORT:Gradient Descent Mathematical optimization First order methods Optimization algorithms and methods Gradient methods
first-order
In mathematics and other formal sciences, first-order or first order most often means either:
* "linear" (a polynomial of degree at most one), as in first-order approximation and other calculus uses, where it is contrasted with "polynomials of hig ...
iterative
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. ...
optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...
for finding a local minimum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given ran ...
of a differentiable function
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
. The idea is to take repeated steps in the opposite direction of the gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
(or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given ran ...
of that function; the procedure is then known as gradient ascent.
Gradient descent is generally attributed to Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. H ...
, who first suggested it in 1847. Jacques Hadamard
Jacques Salomon Hadamard (; 8 December 1865 – 17 October 1963) was a French mathematician who made major contributions in number theory, complex analysis, differential geometry and partial differential equations.
Biography
The son of a teac ...
independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944, with the method becoming increasingly well-studied and used in the following decades.
Description
gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
of at . It follows that, if
:
for a small enough step size or learning rate
In machine learning and statistics, the learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a loss function. Since it influences to what extent newly ...
, then . In other words, the term is subtracted from because we want to move against the gradient, toward the local minimum. With this observation in mind, one starts with a guess for a local minimum of , and considers the sequence such that
:
We have a monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
sequence
:
so, hopefully, the sequence converges to the desired local minimum. Note that the value of the ''step size'' is allowed to change at every iteration. With certain assumptions on the function (for example, convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
and Lipschitz Lipschitz, Lipshitz, or Lipchitz, is an Ashkenazi Jewish (Yiddish/German-Jewish) surname. The surname has many variants, including: Lifshitz ( Lifschitz), Lifshits, Lifshuts, Lefschetz; Lipschitz, Lipshitz, Lipshits, Lopshits, Lipschutz (Lip ...
) and particular choices of (e.g., chosen either via a line search that satisfies the Wolfe conditions, or the Barzilai–Borwein method shown as following),
:
convergence
Convergence may refer to:
Arts and media Literature
*''Convergence'' (book series), edited by Ruth Nanda Anshen
*Convergence (comics), "Convergence" (comics), two separate story lines published by DC Comics:
**A four-part crossover storyline that ...
to a local minimum can be guaranteed. When the function is convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
, all local minima are also global minima, so in this case gradient descent can converge to the global solution.
This process is illustrated in the adjacent picture. Here, is assumed to be defined on the plane, and that its graph has a bowl
A bowl is a typically round dish or container generally used for preparing, serving, or consuming food. The interior of a bowl is characteristically shaped like a spherical cap, with the edges and the bottom forming a seamless curve. This makes ...
shape. The blue curves are the contour line
A contour line (also isoline, isopleth, or isarithm) of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value. It is a plane section of the three-dimensional gr ...
s, that is, the regions on which the value of is constant. A red arrow originating at a point shows the direction of the negative gradient at that point. Note that the (negative) gradient at a point is orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''.
By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in ...
to the contour line going through that point. We see that gradient ''descent'' leads us to the bottom of the bowl, that is, to the point where the value of the function is minimal.
An analogy for understanding gradient descent
The basic intuition behind gradient descent can be illustrated by a hypothetical scenario. A person is stuck in the mountains and is trying to get down (i.e., trying to find the global minimum). There is heavy fog such that visibility is extremely low. Therefore, the path down the mountain is not visible, so they must use local information to find the minimum. They can use the method of gradient descent, which involves looking at the steepness of the hill at their current position, then proceeding in the direction with the steepest descent (i.e., downhill). If they were trying to find the top of the mountain (i.e., the maximum), then they would proceed in the direction of steepest ascent (i.e., uphill). Using this method, they would eventually find their way down the mountain or possibly get stuck in some hole (i.e., local minimum orsaddle point
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the functi ...
), like a mountain lake. However, assume also that the steepness of the hill is not immediately obvious with simple observation, but rather it requires a sophisticated instrument to measure, which the person happens to have at the moment. It takes quite some time to measure the steepness of the hill with the instrument, thus they should minimize their use of the instrument if they wanted to get down the mountain before sunset. The difficulty then is choosing the frequency at which they should measure the steepness of the hill so not to go off track.
In this analogy, the person represents the algorithm, and the path taken down the mountain represents the sequence of parameter settings that the algorithm will explore. The steepness of the hill represents the slope
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is use ...
of the function at that point. The instrument used to measure steepness is differentiation. The direction they choose to travel in aligns with the gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
of the function at that point. The amount of time they travel before taking another measurement is the step size.
Choosing the step size and descent direction
Since using a step size that is too small would slow convergence, and a too large would lead to divergence, finding a good setting of is an important practical problem. Philip Wolfe also advocated using "clever choices of the escentdirection" in practice. Whilst using a direction that deviates from the steepest descent direction may seem counter-intuitive, the idea is that the smaller slope may be compensated for by being sustained over a much longer distance. To reason about this mathematically, consider a direction and step size and consider the more general update: :. Finding good settings of and requires some thought. First of all, we would like the update direction to point downhill. Mathematically, letting denote the angle between and , this requires that To say more, we need more information about the objective function that we are optimising. Under the fairly weak assumption that is continuously differentiable, we may prove that: This inequality implies that the amount by which we can be sure the function is decreased depends on a trade off between the two terms in square brackets. The first term in square brackets measures the angle between the descent direction and the negative gradient. The second term measures how quickly the gradient changes along the descent direction. In principle inequality () could be optimized over and to choose an optimal step size and direction. The problem is that evaluating the second term in square brackets requires evaluating , and extra gradient evaluations are generally expensive and undesirable. Some ways around this problem are: * Forgo the benefits of a clever descent direction by setting , and use line search to find a suitable step-size , such as one that satisfies the Wolfe conditions. A more economic way of choosing learning rates is backtracking line search, a method that has both good theoretical guarantees and experimental results. Note that one does not need to choose to be the gradient; any direction that has positive intersection product with the gradient will result in a reduction of the function value (for a sufficiently small value of ). * Assuming that is twice-differentiable, use its Hessian to estimate Then choose and by optimising inequality (). * Assuming that isLipschitz Lipschitz, Lipshitz, or Lipchitz, is an Ashkenazi Jewish (Yiddish/German-Jewish) surname. The surname has many variants, including: Lifshitz ( Lifschitz), Lifshits, Lifshuts, Lefschetz; Lipschitz, Lipshitz, Lipshits, Lopshits, Lipschutz (Lip ...
, use its Lipschitz constant to bound Then choose and by optimising inequality ().
* Build a custom model of for . Then choose and by optimising inequality ().
* Under stronger assumptions on the function such as convexity
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope ...
, more advanced techniques may be possible.
Usually by following one of the recipes above, convergence
Convergence may refer to:
Arts and media Literature
*''Convergence'' (book series), edited by Ruth Nanda Anshen
*Convergence (comics), "Convergence" (comics), two separate story lines published by DC Comics:
**A four-part crossover storyline that ...
to a local minimum can be guaranteed. When the function is convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
, all local minima are also global minima, so in this case gradient descent can converge to the global solution.
Solution of a linear system
 Gradient descent can be used to solve a system of linear equations
:
reformulated as a quadratic minimization problem.
If the system matrix is real symmetric and positive-definite, an objective function is defined as the quadratic function, with minimization of
:
so that
:
For a general real matrix , linear least squares define
:
In traditional linear least squares for real and the
Gradient descent can be used to solve a system of linear equations
:
reformulated as a quadratic minimization problem.
If the system matrix is real symmetric and positive-definite, an objective function is defined as the quadratic function, with minimization of
:
so that
:
For a general real matrix , linear least squares define
:
In traditional linear least squares for real and the Euclidean norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...
is used, in which case
:
The line search minimization, finding the locally optimal step size on every iteration, can be performed analytically for quadratic functions, and explicit formulas for the locally optimal are known.
For example, for real symmetric and positive-definite matrix , a simple algorithm can be as follows,
:
To avoid multiplying by twice per iteration,
we note that implies , which gives the traditional algorithm,
:
The method is rarely used for solving linear equations, with the conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a c ...
being one of the most popular alternatives. The number of gradient descent iterations is commonly proportional to the spectral condition number
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the inpu ...
of the system matrix (the ratio of the maximum to minimum eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denote ...
of , while the convergence of conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a c ...
is typically determined by a square root of the condition number, i.e., is much faster. Both methods can benefit from preconditioning, where gradient descent may require less assumptions on the preconditioner.
Solution of a non-linear system
Gradient descent can also be used to solve a system of nonlinear equations. Below is an example that shows how to use the gradient descent to solve for three unknown variables, ''x''1, ''x''2, and ''x''3. This example shows one iteration of the gradient descent. Consider the nonlinear system of equations : Let us introduce the associated function : where : One might now define the objective function : which we will attempt to minimize. As an initial guess, let us use : We know that : where theJacobian matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variable ...
is given by
:
We calculate:
:
Thus
:
and
:
 Now, a suitable must be found such that
:
This can be done with any of a variety of line search algorithms. One might also simply guess which gives
:
Evaluating the objective function at this value, yields
:
The decrease from to the next step's value of
:
is a sizable decrease in the objective function. Further steps would reduce its value further until an approximate solution to the system was found.
Now, a suitable must be found such that
:
This can be done with any of a variety of line search algorithms. One might also simply guess which gives
:
Evaluating the objective function at this value, yields
:
The decrease from to the next step's value of
:
is a sizable decrease in the objective function. Further steps would reduce its value further until an approximate solution to the system was found.
Comments
Gradient descent works in spaces of any number of dimensions, even in infinite-dimensional ones. In the latter case, the search space is typically afunction space
In mathematics, a function space is a set of functions between two fixed sets. Often, the domain and/or codomain will have additional structure which is inherited by the function space. For example, the set of functions from any set into a vect ...
, and one calculates the Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on normed spaces. Named after Maurice Fréchet, it is commonly used to generalize the derivative of a real-valued function of a single real variable to the case of a vector-valued ...
of the functional to be minimized to determine the descent direction.
That gradient descent works in any number of dimensions (finite number at least) can be seen as a consequence of the Cauchy-Schwarz inequality. That article proves that the magnitude of the inner (dot) product of two vectors of any dimension is maximized when they are colinear. In the case of gradient descent, that would be when the vector of independent variable adjustments is proportional to the gradient vector of partial derivatives.
The gradient descent can take many iterations to compute a local minimum with a required accuracy
Accuracy and precision are two measures of '' observational error''.
''Accuracy'' is how close a given set of measurements ( observations or readings) are to their '' true value'', while ''precision'' is how close the measurements are to each o ...
, if the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
in different directions is very different for the given function. For such functions, preconditioning, which changes the geometry of the space to shape the function level sets like concentric circles, cures the slow convergence. Constructing and applying preconditioning can be computationally expensive, however.
The gradient descent can be combined with a line search, finding the locally optimal step size on every iteration. Performing the line search can be time-consuming. Conversely, using a fixed small can yield poor convergence.
Methods based on Newton's method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real- ...
and inversion of the Hessian using conjugate gradient
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an itera ...
techniques can be better alternatives. Generally, such methods converge in fewer iterations, but the cost of each iteration is higher. An example is the BFGS method which consists in calculating on every step a matrix by which the gradient vector is multiplied to go into a "better" direction, combined with a more sophisticated line search algorithm, to find the "best" value of For extremely large problems, where the computer-memory issues dominate, a limited-memory method such as L-BFGS should be used instead of BFGS or the steepest descent.
Gradient descent can be viewed as applying Euler's method for solving ordinary differential equations
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast ...
to a gradient flow. In turn, this equation may be derived as an optimal controller for the control system with given in feedback form .
Modifications
Gradient descent can converge to a local minimum and slow down in a neighborhood of asaddle point
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the functi ...
. Even for unconstrained quadratic minimization, gradient descent develops a zig-zag pattern of subsequent iterates as iterations progress, resulting in slow convergence. Multiple modifications of gradient descent have been proposed to address these deficiencies.
Fast gradient methods
Yurii Nesterov
Yurii Nesterov is a Russian mathematician, an internationally recognized expert in convex optimization, especially in the development of efficient algorithms and numerical optimization analysis. He is currently a professor at the University of Lo ...
has proposed a simple modification that enables faster convergence for convex problems and has been since further generalized. For unconstrained smooth problems the method is called the fast gradient method (FGM) or the accelerated gradient method (AGM). Specifically, if the differentiable function is convex and is Lipschitz Lipschitz, Lipshitz, or Lipchitz, is an Ashkenazi Jewish (Yiddish/German-Jewish) surname. The surname has many variants, including: Lifshitz ( Lifschitz), Lifshits, Lifshuts, Lefschetz; Lipschitz, Lipshitz, Lipshits, Lopshits, Lipschutz (Lip ...
, and it is not assumed that is strongly convex, then the error in the objective value generated at each step by the gradient descent method will be bounded by . Using the Nesterov acceleration technique, the error decreases at . It is known that the rate for the decrease of the cost function is optimal for first-order optimization methods. Nevertheless, there is the opportunity to improve the algorithm by reducing the constant factor. The optimized gradient method (OGM) reduces that constant by a factor of two and is an optimal first-order method for large-scale problems.
For constrained or non-smooth problems, Nesterov's FGM is called the fast proximal gradient method (FPGM), an acceleration of the proximal gradient method
Proximal gradient methods are a generalized form of projection used to solve non-differentiable convex optimization problems.
Many interesting problems can be formulated as convex optimization problems of the form
\operatorname\limits_ \sum_^n ...
.
Momentum or ''heavy ball'' method
Trying to break the zig-zag pattern of gradient descent, the ''momentum or heavy ball method'' uses a momentum term in analogy to a heavy ball sliding on the surface of values of the function being minimized, or to mass movement in Newtonian dynamics through aviscous
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the in ...
medium in a conservative force field. Gradient descent with momentum remembers the solution update at each iteration, and determines the next update as a linear combination of the gradient and the previous update. For unconstrained quadratic minimization, a theoretical convergence rate bound of the heavy ball method is asymptotically the same as that for the optimal conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a c ...
.
This technique is used in stochastic gradient descent
Stochastic gradient descent (often abbreviated SGD) is an iterative method for optimizing an objective function with suitable smoothness properties (e.g. differentiable or subdifferentiable). It can be regarded as a stochastic approximation of ...
and as an extension to the backpropagation
In machine learning, backpropagation (backprop, BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions gener ...
algorithms used to train artificial neural network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected unit ...
s. In the direction of updating, stochastic gradient descent adds a stochastic property. The weights can be used to calculate the derivatives.
Extensions
Gradient descent can be extended to handle constraints by including a projection onto the set of constraints. This method is only feasible when the projection is efficiently computable on a computer. Under suitable assumptions, this method converges. This method is a specific case of the forward-backward algorithm for monotone inclusions (which includesconvex programming
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization pro ...
and variational inequalities).
Gradient descent is a special case of mirror descent In mathematics, mirror descent is an iterative optimization algorithm for finding a local minimum of a differentiable function.
It generalizes algorithms such as gradient descent and multiplicative weights.
History
Mirror descent was origin ...
using the squared Euclidean distance as the given Bregman divergence.
See also
* Backtracking line search *Conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a c ...
* Stochastic gradient descent
Stochastic gradient descent (often abbreviated SGD) is an iterative method for optimizing an objective function with suitable smoothness properties (e.g. differentiable or subdifferentiable). It can be regarded as a stochastic approximation of ...
* Rprop
* Delta rule
In machine learning, the delta rule is a gradient descent learning rule for updating the weights of the inputs to artificial neurons in a single-layer neural network. It is a special case of the more general backpropagation algorithm. For a n ...
* Wolfe conditions
* Preconditioning
* Broyden–Fletcher–Goldfarb–Shanno algorithm
In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is an iterative method for solving unconstrained nonlinear optimization problems. Like the related Davidon–Fletcher–Powell method, BFGS determines the ...
* Davidon–Fletcher–Powell formula The Davidon–Fletcher–Powell formula (or DFP; named after William C. Davidon, Roger Fletcher, and Michael J. D. Powell) finds the solution to the secant equation that is closest to the current estimate and satisfies the curvature condition. It ...
* Nelder–Mead method
* Gauss–Newton algorithm
The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum ...
* Hill climbing
numerical analysis, hill climbing is a mathematical optimization technique which belongs to the family of local search. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solutio ...
* Quantum annealing
Quantum annealing (QA) is an optimization process for finding the global minimum of a given objective function over a given set of candidate solutions (candidate states), by a process using quantum fluctuations. Quantum annealing is used mainl ...
* Continuous Local Search
References
Further reading
* * *External links
Using gradient descent in C++, Boost, Ublas for linear regression
Series of Khan Academy videos discusses gradient ascent
* Archived at ttps://ghostarchive.org/varchive/youtube/20211211/IHZwWFHWa-w Ghostarchiveand th
Wayback Machine
{{DEFAULTSORT:Gradient Descent Mathematical optimization First order methods Optimization algorithms and methods Gradient methods