geometric series on:
[Wikipedia]
[Google]
[Amazon]
In
 When summing infinitely many terms, the geometric series can either be convergent or divergent. Convergence means there is a value after summing infinitely many terms, whereas divergence means no value after summing. The convergence of a geometric series can be described depending on the value of a common ratio, see . Grandi's series is an example of a divergent series that can be expressed as , where the initial term is and the common ratio is ; this is because it has three different values.
When summing infinitely many terms, the geometric series can either be convergent or divergent. Convergence means there is a value after summing infinitely many terms, whereas divergence means no value after summing. The convergence of a geometric series can be described depending on the value of a common ratio, see . Grandi's series is an example of a divergent series that can be expressed as , where the initial term is and the common ratio is ; this is because it has three different values.
 As approaches infinity, the absolute value of must be less than one for this sequence of partial sums to converge to a limit. When it does, the series converges absolutely. The infinite series then becomes
for .
This convergence result is widely applied to prove the convergence of other series as well, whenever those series's terms can be bounded from above by a suitable geometric series; that proof strategy is the basis for the
As approaches infinity, the absolute value of must be less than one for this sequence of partial sums to converge to a limit. When it does, the series converges absolutely. The infinite series then becomes
for .
This convergence result is widely applied to prove the convergence of other series as well, whenever those series's terms can be bounded from above by a suitable geometric series; that proof strategy is the basis for the
 In addition to his elegantly simple proof of the divergence of the harmonic series, Nicole Oresme proved that the arithmetico-geometric series known as Gabriel's Staircase,
In the diagram for his geometric proof, similar to the adjacent diagram, shows a two-dimensional geometric series. The first dimension is horizontal, in the bottom row, representing the geometric series with initial value and common ratio
The second dimension is vertical, where the bottom row is a new initial term and each subsequent row above it shrinks according to the same common ratio , making another geometric series with sum ,
This approach generalizes usefully to higher dimensions, and that generalization is described below in .
In addition to his elegantly simple proof of the divergence of the harmonic series, Nicole Oresme proved that the arithmetico-geometric series known as Gabriel's Staircase,
In the diagram for his geometric proof, similar to the adjacent diagram, shows a two-dimensional geometric series. The first dimension is horizontal, in the bottom row, representing the geometric series with initial value and common ratio
The second dimension is vertical, where the bottom row is a new initial term and each subsequent row above it shrinks according to the same common ratio , making another geometric series with sum ,
This approach generalizes usefully to higher dimensions, and that generalization is described below in .
 In addition to finding the area enclosed by a parabola and a line in
In addition to finding the area enclosed by a parabola and a line in
"Geometric Series"
by Michael Schreiber,
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a geometric series is a series
Series may refer to:
People with the name
* Caroline Series (born 1951), English mathematician, daughter of George Series
* George Series (1920–1995), English physicist
Arts, entertainment, and media
Music
* Series, the ordered sets used i ...
summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, the series is a geometric series with common ratio , which converges to the sum of . Each term in a geometric series is the geometric mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite collection of positive real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometri ...
of the term before it and the term after it, in the same way that each term of an arithmetic series
An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference from any succeeding term to its preceding term remains constant throughout the sequence. The constant difference is called common difference of that ...
is the arithmetic mean
In mathematics and statistics, the arithmetic mean ( ), arithmetic average, or just the ''mean'' or ''average'' is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results fr ...
of its neighbors.
While Greek philosopher Zeno's paradoxes
Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through the works of Plato, Aristotle, and later commentators like Simplicius of Cilicia. Zeno de ...
about time and motion (5th century BCE) have been interpreted as involving geometric series, such series were formally studied and applied a century or two later by Greek mathematicians, for example used by Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
to calculate the area inside a parabola (3rd century BCE). Today, geometric series are used in mathematical finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field.
In general, there exist two separate branches of finance that req ...
, calculating areas of fractals, and various computer science topics.
Though geometric series most commonly involve real or complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s, there are also important results and applications for matrix-valued geometric series, function-valued geometric series, adic number geometric series, and most generally geometric series of elements of abstract algebraic fields, ring
(The) Ring(s) may refer to:
* Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry
* To make a sound with a bell, and the sound made by a bell
Arts, entertainment, and media Film and TV
* ''The Ring'' (franchise), a ...
s, and semiring
In abstract algebra, a semiring is an algebraic structure. Semirings are a generalization of rings, dropping the requirement that each element must have an additive inverse. At the same time, semirings are a generalization of bounded distribu ...
s.
Definition and examples
The geometric series is aninfinite series
In mathematics, a series is, roughly speaking, an addition of infinitely many terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathemati ...
derived from a special type of sequence called a geometric progression
A geometric progression, also known as a geometric sequence, is a mathematical sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed number called the ''common ratio''. For example, the s ...
. This means that it is the sum of infinitely many terms of geometric progression: starting from the initial term , and the next one being the initial term multiplied by a constant number known as the common ratio . By multiplying each term with a common ratio continuously, the geometric series can be defined mathematically as
The sum of a finite initial segment of an infinite geometric series is called a finite geometric series, expressed as
When it is often called a growth rate or rate of expansion. When it is often called a decay rate or shrink rate, where the idea that it is a "rate" comes from interpreting as a sort of discrete time variable. When an application area has specialized vocabulary for specific types of growth, expansion, shrinkage, and decay, that vocabulary will also often be used to name parameters of geometric series. In economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
, for instance, rates of increase and decrease of price level
The general price level is a hypothetical measure of overall prices for some set of goods and services (the consumer basket), in an economy or monetary union during a given interval (generally one day), normalized relative to some base set. ...
s are called inflation
In economics, inflation is an increase in the average price of goods and services in terms of money. This increase is measured using a price index, typically a consumer price index (CPI). When the general price level rises, each unit of curre ...
rates and deflation
In economics, deflation is a decrease in the general price level of goods and services. Deflation occurs when the inflation rate falls below 0% and becomes negative. While inflation reduces the value of currency over time, deflation increases i ...
rates, while rates of increase in values
In ethics and social sciences, value denotes the degree of importance of some thing or action, with the aim of determining which actions are best to do or what way is best to live ( normative ethics), or to describe the significance of different a ...
of investment
Investment is traditionally defined as the "commitment of resources into something expected to gain value over time". If an investment involves money, then it can be defined as a "commitment of money to receive more money later". From a broade ...
s include rates of return and interest rate
An interest rate is the amount of interest due per period, as a proportion of the amount lent, deposited, or borrowed (called the principal sum). The total interest on an amount lent or borrowed depends on the principal sum, the interest rate, ...
s.
Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
numbers that have repeated patterns that continue forever can be interpreted as geometric series and thereby converted to expressions of the ratio of two integers. For example, the repeated decimal fraction can be written as the geometric series where the initial term is and the common ratio is .
Convergence of the series and its proof
The convergence of the infinite sequence of partial sums of the infinite geometric series depends on themagnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
of the common ratio alone:
* If , the terms of the series approach zero (becoming smaller and smaller in magnitude) and the sequence of partial sums converge to a limit value of .
* If , the terms of the series become larger and larger in magnitude and the partial sums of the terms also get larger and larger in magnitude, so the series diverges.
* If , the terms of the series become no larger or smaller in magnitude and the sequence of partial sums of the series does not converge. When , all the terms of the series are the same and the grow to infinity. When , the terms take two values and alternately, and therefore the sequence of partial sums of the terms oscillates between the two values and 0. One example can be found in Grandi's series. When and , the partial sums circulate periodically among the values , never converging to a limit. Generally when for any integer and with any , the partial sums of the series will circulate indefinitely with a period of , never converging to a limit.
The rate of convergence shows how the sequence quickly approaches its limit. In the case of the geometric series—the relevant sequence is and its limit is —the rate and order are found via
where represents the order of convergence. Using and choosing the order of convergence gives:
When the series converges, the rate of convergence gets slower as approaches . The pattern of convergence also depends on the sign
A sign is an object, quality, event, or entity whose presence or occurrence indicates the probable presence or occurrence of something else. A natural sign bears a causal relation to its object—for instance, thunder is a sign of storm, or me ...
or complex argument of the common ratio. If and then terms all share the same sign and the partial sums of the terms approach their eventual limit monotonically. If and , adjacent terms in the geometric series alternate between positive and negative, and the partial sums of the terms oscillate above and below their eventual limit . For complex and the converge in a spiraling pattern.
The convergence is proved as follows. The partial sum of the first terms of a geometric series, up to and including the term,
is given by the closed form
where is the common ratio. The case is merely a simple addition, a case of an arithmetic series
An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference from any succeeding term to its preceding term remains constant throughout the sequence. The constant difference is called common difference of that ...
. The formula for the partial sums with can be derived as follows:
for . As approaches 1, polynomial division or L'Hôpital's rule
L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form ...
recovers the case .
ratio test
In mathematics, the ratio test is a convergence tests, test (or "criterion") for the convergent series, convergence of a series (mathematics), series
:\sum_^\infty a_n,
where each term is a real number, real or complex number and is nonzero wh ...
and root test
In mathematics, the root test is a criterion for the convergence (a convergence test) of an infinite series. It depends on the quantity
:\limsup_\sqrt
where a_n are the terms of the series, and states that the series converges absolutely if t ...
for the convergence of infinite series.
Connection to the power series
Like the geometric series, apower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
has one parameter for a common variable raised to successive powers corresponding to the geometric series's , but it has additional parameters one for each term in the series, for the distinct coefficients of each , rather than just a single additional parameter for all terms, the common coefficient of in each term of a geometric series. The geometric series can therefore be considered a class of power series in which the sequence of coefficients satisfies for all and .
This special class of power series plays an important role in mathematics, for instance for the study of ordinary generating functions in combinatorics and the summation
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, pol ...
of divergent series in analysis. Many other power series can be written as transformations and combinations of geometric series, making the geometric series formula a convenient tool for calculating formulas for those power series as well.
As a power series, the geometric series has a radius of convergence
In mathematics, the radius of convergence of a power series is the radius of the largest Disk (mathematics), disk at the Power series, center of the series in which the series Convergent series, converges. It is either a non-negative real number o ...
of 1. This could be seen as a consequence of the Cauchy–Hadamard theorem
In mathematics, the Cauchy–Hadamard theorem is a result in complex analysis named after the French mathematicians Augustin Louis Cauchy and Jacques Hadamard, describing the radius of convergence of a power series. It was published in 1821 by C ...
and the fact that for any or as a consequence of the ratio test
In mathematics, the ratio test is a convergence tests, test (or "criterion") for the convergent series, convergence of a series (mathematics), series
:\sum_^\infty a_n,
where each term is a real number, real or complex number and is nonzero wh ...
for the convergence of infinite series, with implying convergence only for However, both the ratio test and the Cauchy–Hadamard theorem are proven using the geometric series formula as a logically prior result, so such reasoning would be subtly circular.
Background
2,500 years ago, Greek mathematicians believed that an infinitely long list of positive numbers must sum to infinity. Therefore,Zeno of Elea
Zeno of Elea (; ; ) was a pre-Socratic Greek philosopher from Elea, in Southern Italy (Magna Graecia). He was a student of Parmenides and one of the Eleatics. Zeno defended his instructor's belief in monism, the idea that only one single en ...
created a paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true or apparently true premises, leads to a seemingly self-contradictor ...
, demonstrating as follows: in order to walk from one place to another, one must first walk half the distance there, and then half of the remaining distance, and half of that remaining distance, and so on, covering infinitely many intervals before arriving. In doing so, he partitioned a fixed distance into an infinitely long list of halved remaining distances, each with a length greater than zero. Zeno's paradox revealed to the Greeks that their assumption about an infinitely long list of positive numbers needing to add up to infinity was incorrect.
Euclid's '' Elements'' has the distinction of being the world's oldest continuously used mathematical textbook, and it includes a demonstration of the sum of finite geometric series in Book IX, Proposition 35, illustrated in an adjacent figure.
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
in his ''The Quadrature of the Parabola
''Quadrature of the Parabola'' () is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regarding parabolas, culminating in two proofs showing t ...
'' used the sum of a geometric series to compute the area enclosed by a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
and a straight line. Archimedes' theorem states that the total area under the parabola is of the area of the blue triangle. His method was to dissect the area into infinite triangles as shown in the adjacent figure. He determined that each green triangle has the area of the blue triangle, each yellow triangle has the area of a green triangle, and so forth. Assuming that the blue triangle has area 1, then, the total area is the sum of the infinite series
Here the first term represents the area of the blue triangle, the second term is the area of the two green triangles, the third term is the area of the four yellow triangles, and so on. Simplifying the fractions gives
a geometric series with common ratio and its sum is:
:
 In addition to his elegantly simple proof of the divergence of the harmonic series, Nicole Oresme proved that the arithmetico-geometric series known as Gabriel's Staircase,
In the diagram for his geometric proof, similar to the adjacent diagram, shows a two-dimensional geometric series. The first dimension is horizontal, in the bottom row, representing the geometric series with initial value and common ratio
The second dimension is vertical, where the bottom row is a new initial term and each subsequent row above it shrinks according to the same common ratio , making another geometric series with sum ,
This approach generalizes usefully to higher dimensions, and that generalization is described below in .
In addition to his elegantly simple proof of the divergence of the harmonic series, Nicole Oresme proved that the arithmetico-geometric series known as Gabriel's Staircase,
In the diagram for his geometric proof, similar to the adjacent diagram, shows a two-dimensional geometric series. The first dimension is horizontal, in the bottom row, representing the geometric series with initial value and common ratio
The second dimension is vertical, where the bottom row is a new initial term and each subsequent row above it shrinks according to the same common ratio , making another geometric series with sum ,
This approach generalizes usefully to higher dimensions, and that generalization is described below in .
Applications
As mentioned above, the geometric series can be applied in the field ofeconomics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
. This leads to the common ratio of a geometric series that may refer to the rates of increase and decrease of price level
The general price level is a hypothetical measure of overall prices for some set of goods and services (the consumer basket), in an economy or monetary union during a given interval (generally one day), normalized relative to some base set. ...
s are called inflation
In economics, inflation is an increase in the average price of goods and services in terms of money. This increase is measured using a price index, typically a consumer price index (CPI). When the general price level rises, each unit of curre ...
rates and deflation
In economics, deflation is a decrease in the general price level of goods and services. Deflation occurs when the inflation rate falls below 0% and becomes negative. While inflation reduces the value of currency over time, deflation increases i ...
rates; in contrast, the rates of increase in values of investment
Investment is traditionally defined as the "commitment of resources into something expected to gain value over time". If an investment involves money, then it can be defined as a "commitment of money to receive more money later". From a broade ...
s include rates of return and interest rates
An interest rate is the amount of interest due per period, as a proportion of the amount lent, deposited, or borrowed (called the principal sum). The total interest on an amount lent or borrowed depends on the principal sum, the interest rate, ...
. More specifically in mathematical finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field.
In general, there exist two separate branches of finance that req ...
, geometric series can also be applied in time value of money
The time value of money refers to the fact that there is normally a greater benefit to receiving a sum of money now rather than an identical sum later. It may be seen as an implication of the later-developed concept of time preference.
The time ...
; that is to represent the present value
In economics and finance, present value (PV), also known as present discounted value (PDV), is the value of an expected income stream determined as of the date of valuation. The present value is usually less than the future value because money ha ...
s of perpetual annuities, sums of money to be paid each year indefinitely into the future. This sort of calculation is used to compute the annual percentage rate
The term annual percentage rate of charge (APR), corresponding sometimes to a nominal APR and sometimes to an effective APR (EAPR), is the interest rate for a whole year (annualized), rather than just a monthly fee/rate, as applied on a loan, mort ...
of a loan, such as a mortgage loan
A mortgage loan or simply mortgage (), in civil law (legal system), civil law jurisdictions known also as a hypothec loan, is a loan used either by purchasers of real property to raise funds to buy real estate, or by existing property owners t ...
. It can also be used to estimate the present value of expected stock dividends, or the terminal value of a financial asset
A financial asset is a non-physical asset whose value is derived from a contractual claim, such as deposit (finance), bank deposits, bond (finance), bonds, and participations in companies' share capital. Financial assets are usually more market li ...
assuming a stable growth rate. However, the assumption that interest rates are constant is generally incorrect and payments are unlikely to continue forever since the issuer of the perpetual annuity may lose its ability or end its commitment to make continued payments, so estimates like these are only heuristic guidelines for decision making
In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options. It could be either ra ...
rather than scientific predictions of actual current values.
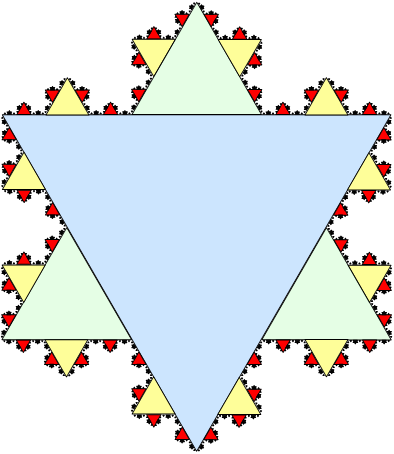
 In addition to finding the area enclosed by a parabola and a line in
In addition to finding the area enclosed by a parabola and a line in Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
' ''The Quadrature of the Parabola
''Quadrature of the Parabola'' () is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regarding parabolas, culminating in two proofs showing t ...
'', the geometric series may also be applied in finding the Koch snowflake
The Koch snowflake (also known as the Koch curve, Koch star, or Koch island) is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a Continuous Cur ...
's area described as the union of infinitely many equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
s (see figure). Each side of the green triangle is exactly the size of a side of the large blue triangle and therefore has exactly the area. Similarly, each yellow triangle has the area of a green triangle, and so forth. All of these triangles can be represented in terms of geometric series: the blue triangle's area is the first term, the three green triangles' area is the second term, the twelve yellow triangles' area is the third term, and so forth. Excluding the initial 1, this series has a common ratio , and by taking the blue triangle as a unit of area, the total area of the snowflake is:
Various topics in computer science may include the application of geometric series in the following:
* Algorithm analysis: analyzing the time complexity
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations ...
of recursive
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in m ...
algorithms (like divide-and-conquer) and in amortized analysis
In computer science, amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case ...
for operations with varying costs, such as dynamic array resizing.
* Data structures: analyzing the space and time complexities of operations in data structures like balanced binary search tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a Rooted tree, rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left ...
s and heaps.
* Computer graphics: crucial in rendering algorithms for anti-aliasing, for mipmap
In computer graphics, a mipmap (''mip'' being an acronym of the Latin phrase ''multum in parvo'', meaning "much in little") is a pre-calculated, optimized sequence of images, each of which has an image resolution which is a factor of two small ...
ping, and for generating fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
s, where the scale of detail varies geometrically.
* Networking and communication: modelling retransmission delays in exponential backoff
Exponential backoff is an algorithm that uses feedback to multiplicatively decrease the rate of some process, in order to gradually find an acceptable rate. These algorithms find usage in a wide range of systems and processes, with radio networ ...
algorithms and are used in data compression
In information theory, data compression, source coding, or bit-rate reduction is the process of encoding information using fewer bits than the original representation. Any particular compression is either lossy or lossless. Lossless compressi ...
and error-correcting codes
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The centra ...
for efficient communication.
* Probabilistic and randomized algorithms: analyzing random walk
In mathematics, a random walk, sometimes known as a drunkard's walk, is a stochastic process that describes a path that consists of a succession of random steps on some Space (mathematics), mathematical space.
An elementary example of a rand ...
s, Markov chain
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally ...
s, and geometric distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions:
* The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \;
* T ...
s, which are essential in probabilistic and randomized algorithm
A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performan ...
s.
Beyond real and complex numbers
While geometric series with real and complex number parameters and are most common, geometric series of more general terms such as functions,matrices
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the ...
, and adic numbers also find application. The mathematical operations used to express a geometric series given its parameters are simply addition and repeated multiplication, and so it is natural, in the context of modern algebra, to define geometric series with parameters from any ring
(The) Ring(s) may refer to:
* Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry
* To make a sound with a bell, and the sound made by a bell
Arts, entertainment, and media Film and TV
* ''The Ring'' (franchise), a ...
or field. Further generalization to geometric series with parameters from semiring
In abstract algebra, a semiring is an algebraic structure. Semirings are a generalization of rings, dropping the requirement that each element must have an additive inverse. At the same time, semirings are a generalization of bounded distribu ...
s is more unusual, but also has applications; for instance, in the study of fixed-point iteration of transformation functions, as in transformations of automata
An automaton (; : automata or automatons) is a relatively self-operating machine, or control mechanism designed to automatically follow a sequence of operations, or respond to predetermined instructions. Some automata, such as bellstrikers i ...
via rational series.
In order to analyze the convergence of these general geometric series, then on top of addition and multiplication, one must also have some metric of distance between partial sums of the series. This can introduce new subtleties into the questions of convergence, such as the distinctions between uniform convergence
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions (f_n) converges uniformly to a limiting function f on a set E as the function domain i ...
and pointwise convergence
In mathematics, pointwise convergence is one of Modes of convergence (annotated index), various senses in which a sequence of function (mathematics), functions can Limit (mathematics), converge to a particular function. It is weaker than uniform co ...
in series of functions, and can lead to strong contrasts with intuitions from the real numbers, such as in the convergence of the series with and to in the 2-adic numbers using the 2-adic absolute value as a convergence metric. In that case, the 2-adic absolute value of the common coefficient is , and while this is counterintuitive from the perspective of real number absolute value (where naturally), it is nonetheless well-justified in the context of p-adic analysis
In mathematics, ''p''-adic analysis is a branch of number theory that studies functions of ''p''-adic numbers. Along with the more classical fields of real and complex analysis, which deal, respectively, with functions on the real and complex ...
.
When the multiplication of the parameters is not commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a pr ...
, as it often is not for matrices or general physical operators, particularly in quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, then the standard way of writing the geometric series,
multiplying from the right, may need to be distinguished from the alternative
multiplying from the left, and also the symmetric
multiplying half on each side. These choices may correspond to important alternatives with different strengths and weaknesses in applications, as in the case of ordering the mutual interferences of drift and diffusion differently at infinitesimal temporal scales in Ito integration and Stratonovitch integration in stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes. This field was created an ...
.
References
* * Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987. * Courant, R. and Robbins, H. "The Geometric Progression." §1.2.3 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 13–14, 1996. * * . * James Stewart (2002). ''Calculus'', 5th ed., Brooks Cole. * Larson, Hostetler, and Edwards (2005). ''Calculus with Analytic Geometry'', 8th ed., Houghton Mifflin Company. * Pappas, T. "Perimeter, Area & the Infinite Series." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 134–135, 1989. * * Roger B. Nelsen (1997). ''Proofs without Words: Exercises in Visual Thinking'', The Mathematical Association of America.History and philosophy
* C. H. Edwards Jr. (1994). ''The Historical Development of the Calculus'', 3rd ed., Springer. . * Eli Maor (1991). ''To Infinity and Beyond: A Cultural History of the Infinite'', Princeton University Press. * Morr Lazerowitz (2000). ''The Structure of Metaphysics (International Library of Philosophy)'', Routledge.Economics
* Carl P. Simon and Lawrence Blume (1994). ''Mathematics for Economists'', W. W. Norton & Company. * Mike Rosser (2003). ''Basic Mathematics for Economists'', 2nd ed., Routledge.Biology
* Edward Batschelet (1992). ''Introduction to Mathematics for Life Scientists'', 3rd ed., Springer. * Richard F. Burton (1998). ''Biology by Numbers: An Encouragement to Quantitative Thinking'', Cambridge University Press.External links
* * * * *"Geometric Series"
by Michael Schreiber,
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an Open source, open-source collection of Interactive computing, interactive programmes called Demonstrations. It is hosted by Wolfram Research. At its launch, it contained 1300 demonstrations but has grown t ...
, 2007.
{{Authority control
Articles containing proofs
Ratios