gas on:
[Wikipedia]
[Google]
[Amazon]
 Gas is a
Gas is a
 There are many mathematical tools available for analyzing gas properties. Boyle's lab equipment allowed the use of just a simple calculation to obtain his analytical results. His results were possible because he was studying gases in relatively low pressure situations where they behaved in an "ideal" manner. These ideal relationships apply to safety calculations for a variety of flight conditions on the materials in use. However, the high technology equipment in use today was designed to help us safely explore the more exotic operating environments where the gases no longer behave in an "ideal" manner. As gases are subjected to extreme conditions, tools to interpret them become more complex, from the
There are many mathematical tools available for analyzing gas properties. Boyle's lab equipment allowed the use of just a simple calculation to obtain his analytical results. His results were possible because he was studying gases in relatively low pressure situations where they behaved in an "ideal" manner. These ideal relationships apply to safety calculations for a variety of flight conditions on the materials in use. However, the high technology equipment in use today was designed to help us safely explore the more exotic operating environments where the gases no longer behave in an "ideal" manner. As gases are subjected to extreme conditions, tools to interpret them become more complex, from the
 When describing a container of gas, the term
When describing a container of gas, the term
 If one could observe a gas under a powerful microscope, one would see a collection of particles without any definite shape or volume that are in more or less random motion. These gas particles only change direction when they collide with another particle or with the sides of the container. This microscopic view of gas is well-described by
If one could observe a gas under a powerful microscope, one would see a collection of particles without any definite shape or volume that are in more or less random motion. These gas particles only change direction when they collide with another particle or with the sides of the container. This microscopic view of gas is well-described by

 The intermolecular attractions and repulsions between two gas molecules depend on the distance between them. The combined attractions and repulsions are well-modelled by the Lennard-Jones potential, which is one of the most extensively studied of all interatomic potentials describing the
The intermolecular attractions and repulsions between two gas molecules depend on the distance between them. The combined attractions and repulsions are well-modelled by the Lennard-Jones potential, which is one of the most extensively studied of all interatomic potentials describing the
 Each one of the assumptions listed below adds to the complexity of the problem's solution. As the density of a gas increases with rising pressure, the intermolecular forces play a more substantial role in gas behavior which results in the ideal gas law no longer providing "reasonable" results. At the upper end of the engine temperature ranges (e.g. combustor sections – 1300 K), the complex fuel particles absorb internal energy by means of rotations and vibrations that cause their specific heats to vary from those of diatomic molecules and noble gases. At more than double that temperature, electronic excitation and dissociation of the gas particles begins to occur causing the pressure to adjust to a greater number of particles (transition from gas to plasma). Finally, all of the thermodynamic processes were presumed to describe uniform gases whose velocities varied according to a fixed distribution. Using a non-equilibrium situation implies the flow field must be characterized in some manner to enable a solution. One of the first attempts to expand the boundaries of the ideal gas law was to include coverage for different thermodynamic processes by adjusting the equation to read ''pVn = constant'' and then varying the ''n'' through different values such as the specific heat ratio, ''γ''.
Real gas effects include those adjustments made to account for a greater range of gas behavior:
* Compressibility effects (''Z'' allowed to vary from 1.0)
*Variable
Each one of the assumptions listed below adds to the complexity of the problem's solution. As the density of a gas increases with rising pressure, the intermolecular forces play a more substantial role in gas behavior which results in the ideal gas law no longer providing "reasonable" results. At the upper end of the engine temperature ranges (e.g. combustor sections – 1300 K), the complex fuel particles absorb internal energy by means of rotations and vibrations that cause their specific heats to vary from those of diatomic molecules and noble gases. At more than double that temperature, electronic excitation and dissociation of the gas particles begins to occur causing the pressure to adjust to a greater number of particles (transition from gas to plasma). Finally, all of the thermodynamic processes were presumed to describe uniform gases whose velocities varied according to a fixed distribution. Using a non-equilibrium situation implies the flow field must be characterized in some manner to enable a solution. One of the first attempts to expand the boundaries of the ideal gas law was to include coverage for different thermodynamic processes by adjusting the equation to read ''pVn = constant'' and then varying the ''n'' through different values such as the specific heat ratio, ''γ''.
Real gas effects include those adjustments made to account for a greater range of gas behavior:
* Compressibility effects (''Z'' allowed to vary from 1.0)
*Variable
 Boyle's law was perhaps the first expression of an equation of state. In 1662 Robert Boyle performed a series of experiments employing a J-shaped glass tube, which was sealed on one end. Mercury was added to the tube, trapping a fixed quantity of air in the short, sealed end of the tube. Then the volume of gas was carefully measured as additional mercury was added to the tube. The pressure of the gas could be determined by the difference between the mercury level in the short end of the tube and that in the long, open end. The image of Boyle's equipment shows some of the exotic tools used by Boyle during his study of gases.
Through these experiments, Boyle noted that the pressure exerted by a gas held at a constant temperature varies inversely with the volume of the gas. For example, if the volume is halved, the pressure is doubled; and if the volume is doubled, the pressure is halved. Given the inverse relationship between pressure and volume, the product of pressure (''P'') and volume (''V'') is a constant (''k'') for a given mass of confined gas as long as the temperature is constant. Stated as a formula, thus is:
:
Because the before and after volumes and pressures of the fixed amount of gas, where the before and after temperatures are the same both equal the constant ''k'', they can be related by the equation:
Boyle's law was perhaps the first expression of an equation of state. In 1662 Robert Boyle performed a series of experiments employing a J-shaped glass tube, which was sealed on one end. Mercury was added to the tube, trapping a fixed quantity of air in the short, sealed end of the tube. Then the volume of gas was carefully measured as additional mercury was added to the tube. The pressure of the gas could be determined by the difference between the mercury level in the short end of the tube and that in the long, open end. The image of Boyle's equipment shows some of the exotic tools used by Boyle during his study of gases.
Through these experiments, Boyle noted that the pressure exerted by a gas held at a constant temperature varies inversely with the volume of the gas. For example, if the volume is halved, the pressure is doubled; and if the volume is doubled, the pressure is halved. Given the inverse relationship between pressure and volume, the product of pressure (''P'') and volume (''V'') is a constant (''k'') for a given mass of confined gas as long as the temperature is constant. Stated as a formula, thus is:
:
Because the before and after volumes and pressures of the fixed amount of gas, where the before and after temperatures are the same both equal the constant ''k'', they can be related by the equation:
 In 1801,
In 1801,
 Thermodynamicists use this factor (''Z'') to alter the ideal gas equation to account for compressibility effects of real gases. This factor represents the ratio of actual to ideal specific volumes. It is sometimes referred to as a "fudge-factor" or correction to expand the useful range of the ideal gas law for design purposes. ''Usually'' this ''Z'' value is very close to unity. The compressibility factor image illustrates how Z varies over a range of very cold temperatures.
Thermodynamicists use this factor (''Z'') to alter the ideal gas equation to account for compressibility effects of real gases. This factor represents the ratio of actual to ideal specific volumes. It is sometimes referred to as a "fudge-factor" or correction to expand the useful range of the ideal gas law for design purposes. ''Usually'' this ''Z'' value is very close to unity. The compressibility factor image illustrates how Z varies over a range of very cold temperatures.
 Particles will, in effect, "stick" to the surface of an object moving through it. This layer of particles is called the boundary layer. At the surface of the object, it is essentially static due to the friction of the surface. The object, with its boundary layer is effectively the new shape of the object that the rest of the molecules "see" as the object approaches. This boundary layer can separate from the surface, essentially creating a new surface and completely changing the flow path. The classical example of this is a stalling airfoil. The delta wing image clearly shows the boundary layer thickening as the gas flows from right to left along the leading edge.
Particles will, in effect, "stick" to the surface of an object moving through it. This layer of particles is called the boundary layer. At the surface of the object, it is essentially static due to the friction of the surface. The object, with its boundary layer is effectively the new shape of the object that the rest of the molecules "see" as the object approaches. This boundary layer can separate from the surface, essentially creating a new surface and completely changing the flow path. The classical example of this is a stalling airfoil. The delta wing image clearly shows the boundary layer thickening as the gas flows from right to left along the leading edge.
 In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic, stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time. The satellite view of weather around Robinson Crusoe Islands illustrates one example.
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic, stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time. The satellite view of weather around Robinson Crusoe Islands illustrates one example.
Animated Gas Lab
Accessed February 2008. *Georgia State University
Accessed February 2008. *Antony Lewi
WordWeb
Accessed February 2008. *Northwestern Michigan Colleg
Accessed February 2008. * {{Authority control Gases *Gas Articles containing video clips
 Gas is a
Gas is a state of matter
In physics, a state of matter is one of the distinct forms in which matter can exist. Four states of matter are observable in everyday life: solid, liquid, gas, and Plasma (physics), plasma.
Different states are distinguished by the ways the ...
that has neither a fixed volume nor a fixed shape and is a compressible fluid. A ''pure gas'' is made up of individual atoms
Atoms are the basic particles of the chemical elements. An atom consists of a nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished from each other ...
(e.g. a noble gas
The noble gases (historically the inert gases, sometimes referred to as aerogens) are the members of Group (periodic table), group 18 of the periodic table: helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), radon (Rn) and, in some ...
like neon
Neon is a chemical element; it has symbol Ne and atomic number 10. It is the second noble gas in the periodic table. Neon is a colorless, odorless, inert monatomic gas under standard conditions, with approximately two-thirds the density of ...
) or molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemi ...
s of either a single type of atom ( elements such as oxygen
Oxygen is a chemical element; it has chemical symbol, symbol O and atomic number 8. It is a member of the chalcogen group (periodic table), group in the periodic table, a highly reactivity (chemistry), reactive nonmetal (chemistry), non ...
) or from different atoms ( compounds such as carbon dioxide
Carbon dioxide is a chemical compound with the chemical formula . It is made up of molecules that each have one carbon atom covalent bond, covalently double bonded to two oxygen atoms. It is found in a gas state at room temperature and at norma ...
). A ''gas mixture
In chemistry, a mixture is a material made up of two or more different chemical substances which can be separated by physical method. It is an impure substance made up of 2 or more elements or compounds mechanically mixed together in any proporti ...
'', such as air, contains a variety of pure gases. What distinguishes gases from liquids and solids is the vast separation of the individual gas particle
In the physical sciences, a particle (or corpuscle in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass.
They vary greatly in size or quantity, from s ...
s. This separation can make some gases invisible to the human observer.
The gaseous state of matter occurs between the liquid and plasma states, the latter of which provides the upper-temperature boundary for gases. Bounding the lower end of the temperature scale lie degenerative quantum gases which are gaining increasing attention.
High-density atomic gases super-cooled to very low temperatures are classified by their statistical behavior as either Bose gases or Fermi gases. For a comprehensive listing of these exotic states of matter, see list of states of matter.
Elemental gases
The onlychemical elements
A chemical element is a chemical substance whose atoms all have the same number of protons. The number of protons is called the atomic number of that element. For example, oxygen has an atomic number of 8: each oxygen atom has 8 protons in i ...
that are stable diatomic
Diatomic molecules () are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen () or oxygen (), then it is said to be homonuclear mol ...
homonuclear molecular gases at STP are hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
(H2), nitrogen
Nitrogen is a chemical element; it has Symbol (chemistry), symbol N and atomic number 7. Nitrogen is a Nonmetal (chemistry), nonmetal and the lightest member of pnictogen, group 15 of the periodic table, often called the Pnictogen, pnictogens. ...
(N2), oxygen
Oxygen is a chemical element; it has chemical symbol, symbol O and atomic number 8. It is a member of the chalcogen group (periodic table), group in the periodic table, a highly reactivity (chemistry), reactive nonmetal (chemistry), non ...
(O2), and two halogens
The halogens () are a group (periodic table), group in the periodic table consisting of six chemically related chemical element, elements: fluorine (F), chlorine (Cl), bromine (Br), iodine (I), and the radioactive elements astatine (At) and ten ...
: fluorine
Fluorine is a chemical element; it has Chemical symbol, symbol F and atomic number 9. It is the lightest halogen and exists at Standard temperature and pressure, standard conditions as pale yellow Diatomic molecule, diatomic gas. Fluorine is extre ...
(F2) and chlorine
Chlorine is a chemical element; it has Symbol (chemistry), symbol Cl and atomic number 17. The second-lightest of the halogens, it appears between fluorine and bromine in the periodic table and its properties are mostly intermediate between ...
(Cl2). When grouped with the monatomic
In physics and chemistry, "monatomic" is a combination of the words "mono" and "atomic", and means "single atom". It is usually applied to gases: a monatomic gas is a gas in which atoms are not bound to each other. Examples at standard conditions ...
noble gases
The noble gases (historically the inert gases, sometimes referred to as aerogens) are the members of group 18 of the periodic table: helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), radon (Rn) and, in some cases, oganesson (Og) ...
– helium
Helium (from ) is a chemical element; it has chemical symbol, symbol He and atomic number 2. It is a colorless, odorless, non-toxic, inert gas, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling point is ...
(He), neon
Neon is a chemical element; it has symbol Ne and atomic number 10. It is the second noble gas in the periodic table. Neon is a colorless, odorless, inert monatomic gas under standard conditions, with approximately two-thirds the density of ...
(Ne), argon
Argon is a chemical element; it has symbol Ar and atomic number 18. It is in group 18 of the periodic table and is a noble gas. Argon is the third most abundant gas in Earth's atmosphere, at 0.934% (9340 ppmv). It is more than twice as abu ...
(Ar), krypton
Krypton (from 'the hidden one') is a chemical element; it has symbol (chemistry), symbol Kr and atomic number 36. It is a colorless, odorless noble gas that occurs in trace element, trace amounts in the Earth's atmosphere, atmosphere and is of ...
(Kr), xenon
Xenon is a chemical element; it has symbol Xe and atomic number 54. It is a dense, colorless, odorless noble gas found in Earth's atmosphere in trace amounts. Although generally unreactive, it can undergo a few chemical reactions such as the ...
(Xe), and radon
Radon is a chemical element; it has symbol Rn and atomic number 86. It is a radioactive noble gas and is colorless and odorless. Of the three naturally occurring radon isotopes, only Rn has a sufficiently long half-life (3.825 days) for it to b ...
(Rn) – these gases are referred to as "elemental gases".
Etymology
The word ''gas'' was first used by the early 17th-century Flemish chemist Jan Baptist van Helmont. He identifiedcarbon dioxide
Carbon dioxide is a chemical compound with the chemical formula . It is made up of molecules that each have one carbon atom covalent bond, covalently double bonded to two oxygen atoms. It is found in a gas state at room temperature and at norma ...
, the first known gas other than air. Van Helmont's word appears to have been simply a phonetic transcription of the Ancient Greek
Ancient Greek (, ; ) includes the forms of the Greek language used in ancient Greece and the classical antiquity, ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Greek ...
word – the ''g'' in Dutch being pronounced like ''ch'' in "loch
''Loch'' ( ) is a word meaning "lake" or "inlet, sea inlet" in Scottish Gaelic, Scottish and Irish Gaelic, subsequently borrowed into English. In Irish contexts, it often appears in the anglicized form "lough". A small loch is sometimes calle ...
" (voiceless velar fricative, ) – in which case Van Helmont simply was following the established alchemical usage first attested in the works of Paracelsus
Paracelsus (; ; 1493 – 24 September 1541), born Theophrastus von Hohenheim (full name Philippus Aureolus Theophrastus Bombastus von Hohenheim), was a Swiss physician, alchemist, lay theologian, and philosopher of the German Renaissance.
H ...
. According to Paracelsus's terminology, ''chaos'' meant something like .
An alternative story is that Van Helmont's term was derived from "''gahst'' (or ''geist''), which signifies a ghost or spirit". That story is given no credence by the editors of the ''Oxford English Dictionary
The ''Oxford English Dictionary'' (''OED'') is the principal historical dictionary of the English language, published by Oxford University Press (OUP), a University of Oxford publishing house. The dictionary, which published its first editio ...
''. In contrast, the French-American historian Jacques Barzun
Jacques Martin Barzun (; November 30, 1907 – October 25, 2012) was a French-born American historian known for his studies of the history of ideas and cultural history. He wrote about a wide range of subjects, including baseball, mystery novels, ...
speculated that Van Helmont had borrowed the word from the German , meaning the froth resulting from fermentation
Fermentation is a type of anaerobic metabolism which harnesses the redox potential of the reactants to make adenosine triphosphate (ATP) and organic end products. Organic molecules, such as glucose or other sugars, are catabolized and reduce ...
.
Physical characteristics
Because most gases are difficult to observe directly, they are described through the use of four physical properties ormacroscopic
The macroscopic scale is the length scale on which objects or phenomena are large enough to be visible with the naked eye, without magnifying optical instruments. It is the opposite of microscopic.
Overview
When applied to physical phenome ...
characteristics: pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
, volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
, number of particles
In thermodynamics, the particle number (symbol ) of a thermodynamic system is the number of constituent particles in that system. The particle number is a fundamental thermodynamic property which is conjugate to the chemical potential. Unlike m ...
(chemists group them by moles) and temperature. These four characteristics were repeatedly observed by scientists such as Robert Boyle, Jacques Charles, John Dalton
John Dalton (; 5 or 6 September 1766 – 27 July 1844) was an English chemist, physicist and meteorologist. He introduced the atomic theory into chemistry. He also researched Color blindness, colour blindness; as a result, the umbrella term ...
, Joseph Gay-Lussac and Amedeo Avogadro for a variety of gases in various settings. Their detailed studies ultimately led to a mathematical relationship among these properties expressed by the ideal gas law (see section below).
Gas particles are widely separated from one another, and consequently, have weaker intermolecular bonds than liquids or solids. These intermolecular forces result from electrostatic interactions between gas particles. Like-charged areas of different gas particles repel, while oppositely charged regions of different gas particles attract one another; gases that contain permanently charged ions
An ion () is an atom or molecule with a net electrical charge. The charge of an electron is considered to be negative by convention and this charge is equal and opposite to the charge of a proton, which is considered to be positive by convent ...
are known as plasmas. Gaseous compounds with polar covalent bonds contain permanent charge imbalances and so experience relatively strong intermolecular forces, although the compound's net charge remains neutral. Transient, randomly induced charges exist across non-polar covalent bond
A covalent bond is a chemical bond that involves the sharing of electrons to form electron pairs between atoms. These electron pairs are known as shared pairs or bonding pairs. The stable balance of attractive and repulsive forces between atom ...
s of molecules and electrostatic interactions caused by them are referred to as Van der Waals force
In molecular physics and chemistry, the van der Waals force (sometimes van der Waals' force) is a distance-dependent interaction between atoms or molecules. Unlike ionic or covalent bonds, these attractions do not result from a chemical elec ...
s. The interaction of these intermolecular forces varies within a substance which determines many of the physical properties unique to each gas. A comparison of ''boiling points'' for compounds formed by ionic and covalent bonds leads us to this conclusion.
Compared to the other states of matter, gases have low density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
and viscosity
Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e ...
. Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
and temperature influence the particles within a certain volume. This variation in particle separation and speed is referred to as ''compressibility''. This particle separation and size influences optical properties of gases as can be found in the following list of refractive indices. Finally, gas particles spread apart or diffuse in order to homogeneously distribute themselves throughout any container.
Macroscopic view of gases
When observing gas, it is typical to specify a frame of reference or length scale. A larger length scale corresponds to amacroscopic
The macroscopic scale is the length scale on which objects or phenomena are large enough to be visible with the naked eye, without magnifying optical instruments. It is the opposite of microscopic.
Overview
When applied to physical phenome ...
or global point of view of the gas. This region (referred to as a volume) must be sufficient in size to contain a large sampling of gas particles. The resulting statistical analysis of this sample size produces the "average" behavior (i.e. velocity, temperature or pressure) of all the gas particles within the region. In contrast, a smaller length scale corresponds to a microscopic or particle point of view.
Macroscopically, the gas characteristics measured are either in terms of the gas particles themselves (velocity, pressure, or temperature) or their surroundings (volume). For example, Robert Boyle studied pneumatic chemistry for a small portion of his career. One of his experiments related the macroscopic
The macroscopic scale is the length scale on which objects or phenomena are large enough to be visible with the naked eye, without magnifying optical instruments. It is the opposite of microscopic.
Overview
When applied to physical phenome ...
properties of pressure and volume of a gas. His experiment used a J-tube manometer
Pressure measurement is the measurement of an applied force by a fluid (liquid or gas) on a surface. Pressure is typically measured in units of force per unit of surface area. Many techniques have been developed for the measurement of pressu ...
which looks like a test tube
A test tube, also known as a culture tube or sample tube, is a common piece of laboratory glassware consisting of a finger-like length of glass or clear plastic tubing, open at the top and closed at the bottom.
Test tubes are usually placed in s ...
in the shape of the letter J. Boyle trapped an inert gas in the closed end of the test tube with a column of mercury, thereby making the number of particles and the temperature constant. He observed that when the pressure was increased in the gas, by adding more mercury to the column, the trapped gas' volume decreased (this is known as an inverse relationship). Furthermore, when Boyle multiplied the pressure and volume of each observation, the product was constant. This relationship held for every gas that Boyle observed leading to the law, (PV=k), named to honor his work in this field.
 There are many mathematical tools available for analyzing gas properties. Boyle's lab equipment allowed the use of just a simple calculation to obtain his analytical results. His results were possible because he was studying gases in relatively low pressure situations where they behaved in an "ideal" manner. These ideal relationships apply to safety calculations for a variety of flight conditions on the materials in use. However, the high technology equipment in use today was designed to help us safely explore the more exotic operating environments where the gases no longer behave in an "ideal" manner. As gases are subjected to extreme conditions, tools to interpret them become more complex, from the
There are many mathematical tools available for analyzing gas properties. Boyle's lab equipment allowed the use of just a simple calculation to obtain his analytical results. His results were possible because he was studying gases in relatively low pressure situations where they behaved in an "ideal" manner. These ideal relationships apply to safety calculations for a variety of flight conditions on the materials in use. However, the high technology equipment in use today was designed to help us safely explore the more exotic operating environments where the gases no longer behave in an "ideal" manner. As gases are subjected to extreme conditions, tools to interpret them become more complex, from the Euler equations
In mathematics and physics, many topics are eponym, named in honor of Swiss mathematician Leonhard Euler (1707–1783), who made many important discoveries and innovations. Many of these items named after Euler include their own unique function, e ...
for inviscid flow to the Navier–Stokes equations
The Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician Georg ...
that fully account for viscous effects. This advanced math, including statistics and multivariable calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables ('' mult ...
, adapted to the conditions of the gas system in question, makes it possible to solve such complex dynamic situations as space vehicle reentry. An example is the analysis of the space shuttle reentry pictured to ensure the material properties under this loading condition are appropriate. In this flight situation, the gas is no longer behaving ideally.
Pressure
The symbol used to represent pressure in equations is "p" or "P" with SI units of pascals.pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
(or absolute pressure) refers to the average force per unit area that the gas exerts on the surface of the container. Within this volume, it is sometimes easier to visualize the gas particles moving in straight lines until they collide with the container (see diagram at top). The force imparted by a gas particle into the container during this collision is the change in momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
of the particle. During a collision only the normal component of velocity changes. A particle traveling parallel to the wall does not change its momentum. Therefore, the average force on a surface must be the average change in linear momentum from all of these gas particle collisions.
Pressure is the sum of all the normal components of force exerted by the particles impacting the walls of the container divided by the surface area of the wall.
Temperature
The symbol used to represent ''temperature'' in equations is ''T'' with SI units ofkelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By de ...
s.
The speed of a gas particle is proportional to its absolute temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion.
Thermodynamic temperature is typically expres ...
. The volume of the balloon in the video shrinks when the trapped gas particles slow down with the addition of extremely cold nitrogen. The temperature of any physical system
A physical system is a collection of physical objects under study. The collection differs from a set: all the objects must coexist and have some physical relationship.
In other words, it is a portion of the physical universe chosen for analys ...
is related to the motions of the particles (molecules and atoms) which make up the assystem. In statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
, temperature is the measure of the average kinetic energy stored in a molecule (also known as the thermal energy). The methods of storing this energy are dictated by the degrees of freedom
In many scientific fields, the degrees of freedom of a system is the number of parameters of the system that may vary independently. For example, a point in the plane has two degrees of freedom for translation: its two coordinates; a non-infinite ...
of the molecule itself ( energy modes). Thermal (kinetic) energy added to a gas or liquid (an endothermic
An endothermic process is a chemical or physical process that absorbs heat from its surroundings. In terms of thermodynamics, it is a thermodynamic process with an increase in the enthalpy (or internal energy ) of the system.Oxtoby, D. W; Gillis, ...
process) produces translational, rotational, and vibrational motion. In contrast, a solid can only increase its internal energy by exciting additional vibrational modes, as the crystal lattice structure prevents both translational and rotational motion. These heated gas molecules have a greater speed range (wider distribution of speeds) with a higher average or ''mean'' speed. The variance of this distribution is due to the speeds of individual particles constantly varying, due to repeated collisions with other particles. The speed range can be described by the Maxwell–Boltzmann distribution. Use of this distribution implies ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
es near thermodynamic equilibrium for the system of particles being considered.
Specific volume
The symbol used to represent specific volume in equations is "v" with SI units of cubic meters per kilogram. The symbol used to represent volume in equations is "V" with SI units of cubic meters. When performing a thermodynamic analysis, it is typical to speak ofintensive and extensive properties
Physical or chemical properties of materials and systems can often be categorized as being either intensive or extensive, according to how the property changes when the size (or extent) of the system changes.
The terms "intensive and extensiv ...
. Properties which depend on the amount of gas (either by mass or volume) are called ''extensive'' properties, while properties that do not depend on the amount of gas are called intensive properties. Specific volume is an example of an intensive property because it is the ratio of volume occupied by a ''unit of mass'' of a gas that is identical throughout a system at equilibrium. 1000 atoms a gas occupy the same space as any other 1000 atoms for any given temperature and pressure. This concept is easier to visualize for solids such as iron which are incompressible compared to gases. However, volume itself --- not specific --- is an extensive property.
Density
The symbol used to represent density in equations is ρ (rho) with SI units of kilograms per cubic meter. This term is the reciprocal of specific volume. Since gas molecules can move freely within a container, their mass is normally characterized by density. Density is the amount of mass per unit volume of a substance, or the inverse of specific volume. For gases, the density can vary over a wide range because the particles are free to move closer together when constrained by pressure or volume. This variation of density is referred to as compressibility. Like pressure and temperature, density is a state variable of a gas and the change in density during any process is governed by the laws of thermodynamics. For a static gas, the density is the same throughout the entire container. Density is therefore a scalar quantity. It can be shown by kinetic theory that the density is inversely proportional to the size of the container in which a fixed mass of gas is confined. In this case of a fixed mass, the density decreases as the volume increases.Microscopic view of gases
statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
, but it can be described by many different theories. The ''kinetic theory of gases'', which makes the assumption that these collisions are perfectly elastic
Elastic is a word often used to describe or identify certain types of elastomer, Elastic (notion), elastic used in garments or stretch fabric, stretchable fabrics.
Elastic may also refer to:
Alternative name
* Rubber band, ring-shaped band of rub ...
, does not account for intermolecular forces of attraction and repulsion.
Kinetic theory of gases
Kinetic theory provides insight into the macroscopic properties of gases by considering their molecular composition and motion. Starting with the definitions ofmomentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
and kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
, one can use the conservation of momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
and geometric relationships of a cube to relate macroscopic system properties of temperature and pressure to the microscopic property of kinetic energy per molecule. The theory provides averaged values for these two properties.
The ''kinetic theory of gases'' can help explain how the system (the collection of gas particles being considered) responds to changes in temperature, with a corresponding change in ''kinetic energy''.
For example: Imagine you have a sealed container of a fixed-size (a ''constant'' volume), containing a fixed-number of gas particles; starting from absolute zero
Absolute zero is the lowest possible temperature, a state at which a system's internal energy, and in ideal cases entropy, reach their minimum values. The absolute zero is defined as 0 K on the Kelvin scale, equivalent to −273.15 ° ...
(the theoretical temperature at which atoms or molecules have no thermal energy, i.e. are not moving or vibrating), you begin to add energy to the system by heating the container, so that energy transfers to the particles inside. Once their internal energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accoun ...
is above zero-point energy
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly Quantum fluctuation, fluctuate in their lowest energy state as described by the Heisen ...
, meaning their ''kinetic'' energy (also known as ''thermal'' energy) is non-zero, the gas particles will begin to move around the container. As the box is further heated (as more energy is added), the individual particles increase their average speed as the system's total internal energy increases. The higher average-speed of all the particles leads to a greater rate at which collisions happen (i.e. greater number of collisions per unit of time), between particles and the container, as well as between the particles themselves.
The ''macro''scopic, measurable quantity of ''pressure,'' is the direct result of these ''micro''scopic particle collisions with the surface, over which, individual molecules exert a small force, each contributing to the total force applied within a specific area. (''Read .'')
Likewise, the macroscopically measurable quantity of ''temperature'', is a quantification of the overall amount of ''motion, or kinetic energy'' that the particles exhibit. (''Read .'')
Thermal motion and statistical mechanics
In the ''kinetic theory of gases'', kinetic energy is assumed to purely consist of linear translations according to a speed distribution of ''particles'' in the system. However, in ''real gases'' and other real substances, the motions which define the kinetic energy of a system (which collectively determine the temperature), are much more complex than simple lineartranslation
Translation is the communication of the semantics, meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The English la ...
due to the more complex structure of molecules, compared to single atoms which act similarly to point-masses. In real thermodynamic systems, quantum phenomena play a large role in determining thermal motions. The random, thermal motions (kinetic energy) in molecules is a combination of a finite set of possible motions including translation, rotation, and vibration
Vibration () is a mechanical phenomenon whereby oscillations occur about an equilibrium point. Vibration may be deterministic if the oscillations can be characterised precisely (e.g. the periodic motion of a pendulum), or random if the os ...
. This finite range of possible motions, along with the finite set of molecules in the system, leads to a finite number of '' microstates'' within the system; we call the set of all microstates an '' ensemble.'' Specific to atomic or molecular systems, we could potentially have three different kinds of ensemble, depending on the situation: microcanonical ensemble
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it canno ...
, canonical ensemble, or grand canonical ensemble
In statistical mechanics, the grand canonical ensemble (also known as the macrocanonical ensemble) is the statistical ensemble that is used to represent the possible states of a mechanical system of particles that are in thermodynamic equilibri ...
. Specific combinations of microstates within an ensemble are how we truly define ''macrostate'' of the system (temperature, pressure, energy, etc.). In order to do that, we must first count all microstates though use of a '' partition function.'' The use of statistical mechanics and the partition function is an important tool throughout all of physical chemistry, because it is the key to connection between the microscopic states of a system and the macroscopic variables which we can measure, such as temperature, pressure, heat capacity, internal energy, enthalpy, and entropy, just to name a few. (''Read'': Partition function Meaning and significance)
Using the partition function to find the energy of a molecule, or system of molecules, can sometimes be approximated by the Equipartition theorem
In classical physics, classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energy, energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, ...
, which greatly-simplifies calculation. However, this method assumes all molecular degrees of freedom
In many scientific fields, the degrees of freedom of a system is the number of parameters of the system that may vary independently. For example, a point in the plane has two degrees of freedom for translation: its two coordinates; a non-infinite ...
are equally populated, and therefore equally utilized for storing energy within the molecule. It would imply that internal energy changes linearly with temperature, which is not the case. This ignores the fact that heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity is a ...
changes with temperature, due to certain degrees of freedom being unreachable (a.k.a. "frozen out") at lower temperatures. As internal energy of molecules increases, so does the ability to store energy within additional degrees of freedom. As more degrees of freedom become available to hold energy, this causes the molar heat capacity of the substance to increase.
Brownian motion
Brownian motion is the mathematical model used to describe the random movement of particles suspended in a fluid. The gas particle animation, using pink and green particles, illustrates how this behavior results in the spreading out of gases (entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
). These events are also described by particle theory.
Since it is at the limit of (or beyond) current technology to observe individual gas particles (atoms or molecules), only theoretical calculations give suggestions about how they move, but their motion is different from Brownian motion because Brownian motion involves a smooth drag due to the frictional force of many gas molecules, punctuated by violent collisions of an individual (or several) gas molecule(s) with the particle. The particle (generally consisting of millions or billions of atoms) thus moves in a jagged course, yet not so jagged as would be expected if an individual gas molecule were examined.
Intermolecular forces - the primary difference between ''Real'' and ''Ideal'' gases
Forces between two or more molecules or atoms, either attractive or repulsive, are called ''intermolecular forces''. Intermolecular forces are experienced by molecules when they are within physical proximity of one another. These forces are very important for properly modeling molecular systems, as to accurately predict the microscopic behavior of molecules in ''any'' system, and therefore, are necessary for accurately predicting the physical properties of gases (and liquids) across wide variations in physical conditions. Arising from the study ofphysical chemistry
Physical chemistry is the study of macroscopic and microscopic phenomena in chemical systems in terms of the principles, practices, and concepts of physics such as motion, energy, force, time, thermodynamics, quantum chemistry, statistical mech ...
, one of the most prominent intermolecular forces throughout physics, are ''van der Waals force
In molecular physics and chemistry, the van der Waals force (sometimes van der Waals' force) is a distance-dependent interaction between atoms or molecules. Unlike ionic or covalent bonds, these attractions do not result from a chemical elec ...
s''. Van der Waals forces play a key role in determining nearly all physical properties of fluids such as viscosity
Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e ...
, flow rate, and gas dynamics (see physical characteristics section). The van der Waals interactions between gas molecules, is the reason why modeling a "real gas" is more mathematically difficult than an "''ideal'' gas". Ignoring these proximity-dependent forces allows a real gas to be treated like an ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
, which greatly simplifies calculation.
 The intermolecular attractions and repulsions between two gas molecules depend on the distance between them. The combined attractions and repulsions are well-modelled by the Lennard-Jones potential, which is one of the most extensively studied of all interatomic potentials describing the
The intermolecular attractions and repulsions between two gas molecules depend on the distance between them. The combined attractions and repulsions are well-modelled by the Lennard-Jones potential, which is one of the most extensively studied of all interatomic potentials describing the potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
of molecular systems. Due to the general applicability and importance, the Lennard-Jones model system is often referred to as 'Lennard-Jonesium'. The Lennard-Jones potential between molecules can be broken down into two separate components: a long-distance attraction due to the London dispersion force, and a short-range repulsion due to electron-electron exchange interaction (which is related to the Pauli exclusion principle).
When two molecules are relatively distant (meaning they have a high ''potential'' energy), they experience a weak attracting force, causing them to move toward each other, lowering their potential energy. However, if the molecules are ''too far'' away, then they would not experience attractive force of any significance. Additionally, if the molecules get ''too close'' then they will collide, and experience a ''very high'' repulsive force (modelled by Hard spheres) which is a ''much stronger force'' than the attractions, so that any attraction due to proximity is disregarded.
As two molecules approach each other, from a distance that is ''neither'' too-far, ''nor'' too-close, their attraction increases as the magnitude of their potential energy increases (becoming more negative), and lowers their total internal energy. The attraction causing the molecules to get closer, can only happen if the molecules remain in proximity for the duration of time it takes to physically ''move'' closer. Therefore, the attractive forces are strongest when the molecules move at ''low speeds''. This means that the attraction between molecules is ''significant'' when gas temperatures is ''low''. However, if you were to isothermally compress this cold gas into a small volume, ''forcing'' the molecules into close proximity, and raising the pressure, the repulsions will begin to dominate over the attractions, as the rate at which collisions are happening will increase significantly. Therefore, at low temperatures, and low pressures, ''attraction'' is the dominant intermolecular interaction.
If two molecules are moving at high speeds, in arbitrary directions, along non-intersecting paths, then they will not spend enough time in proximity to be affected by the attractive London-dispersion force. If the two molecules collide, they are moving too fast and their kinetic energy will be much greater than any attractive potential energy, so they will only experience repulsion upon colliding. Thus, attractions between molecules can be neglected at ''high temperatures'' due to high speeds. At high temperatures, and high pressures, ''repulsion'' is the dominant intermolecular interaction.
Accounting for the above stated effects which cause these attractions and repulsions, real gases, delineate from the ''ideal gas'' model by the following generalization:
* At low temperatures, and low pressures, the volume occupied by a real gas, is ''less than'' the volume predicted by the ideal gas law.
* At high temperatures, and high pressures, the volume occupied by a real gas, is ''greater than'' the volume predicted by the ideal gas law.
Mathematical models
An ''equation of state'' (for gases) is a mathematical model used to roughly describe or predict the state properties of a gas. At present, there is no single equation of state that accurately predicts the properties of all gases under all conditions. Therefore, a number of much more accurate equations of state have been developed for gases in specific temperature and pressure ranges. The "gas models" that are most widely discussed are "perfect gas", "ideal gas" and "real gas". Each of these models has its own set of assumptions to facilitate the analysis of a given thermodynamic system. Each successive model expands the temperature range of coverage to which it applies.Ideal and perfect gas
Theequation of state
In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most mo ...
for an ideal or perfect gas is the ideal gas law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stat ...
and reads
:
where ''P'' is the pressure, ''V'' is the volume, ''n'' is amount of gas (in mol units), ''R'' is the universal gas constant, 8.314 J/(mol K), and ''T'' is the temperature. Written this way, it is sometimes called the "chemist's version", since it emphasizes the number of molecules ''n''. It can also be written as
:
where is the specific gas constant for a particular gas, in units J/(kg K), and ρ = m/V is density. This notation is the "gas dynamicist's" version, which is more practical in modeling of gas flows involving acceleration without chemical reactions.
The ideal gas law does not make an assumption about the heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity is a ...
of a gas. In the most general case, the specific heat is a function of both temperature and pressure. If the pressure-dependence is neglected (and possibly the temperature-dependence as well) in a particular application, sometimes the gas is said to be a perfect gas
In physics, engineering, and physical chemistry, a perfect gas is a theoretical gas model that differs from real gases in specific ways that makes certain calculations easier to handle. In all perfect gas models, intermolecular forces are neglecte ...
, although the exact assumptions may vary depending on the author and/or field of science.
For an ideal gas, the ideal gas law applies without restrictions on the specific heat. An ideal gas is a simplified "real gas" with the assumption that the compressibility factor
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas ...
''Z'' is set to 1 meaning that this pneumatic ratio remains constant. A compressibility factor of one also requires the four state variables to follow the ideal gas law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stat ...
.
This approximation is more suitable for applications in engineering although simpler models can be used to produce a "ball-park" range as to where the real solution should lie. An example where the "ideal gas approximation" would be suitable would be inside a combustion chamber
A combustion chamber is part of an internal combustion engine in which the air–fuel ratio, fuel/air mix is burned. For steam engines, the term has also been used for an extension of the Firebox (steam engine), firebox which is used to allow a mo ...
of a jet engine
A jet engine is a type of reaction engine, discharging a fast-moving jet (fluid), jet of heated gas (usually air) that generates thrust by jet propulsion. While this broad definition may include Rocket engine, rocket, Pump-jet, water jet, and ...
. It may also be useful to keep the elementary reactions and chemical dissociations for calculating emissions.
Real gas
 Each one of the assumptions listed below adds to the complexity of the problem's solution. As the density of a gas increases with rising pressure, the intermolecular forces play a more substantial role in gas behavior which results in the ideal gas law no longer providing "reasonable" results. At the upper end of the engine temperature ranges (e.g. combustor sections – 1300 K), the complex fuel particles absorb internal energy by means of rotations and vibrations that cause their specific heats to vary from those of diatomic molecules and noble gases. At more than double that temperature, electronic excitation and dissociation of the gas particles begins to occur causing the pressure to adjust to a greater number of particles (transition from gas to plasma). Finally, all of the thermodynamic processes were presumed to describe uniform gases whose velocities varied according to a fixed distribution. Using a non-equilibrium situation implies the flow field must be characterized in some manner to enable a solution. One of the first attempts to expand the boundaries of the ideal gas law was to include coverage for different thermodynamic processes by adjusting the equation to read ''pVn = constant'' and then varying the ''n'' through different values such as the specific heat ratio, ''γ''.
Real gas effects include those adjustments made to account for a greater range of gas behavior:
* Compressibility effects (''Z'' allowed to vary from 1.0)
*Variable
Each one of the assumptions listed below adds to the complexity of the problem's solution. As the density of a gas increases with rising pressure, the intermolecular forces play a more substantial role in gas behavior which results in the ideal gas law no longer providing "reasonable" results. At the upper end of the engine temperature ranges (e.g. combustor sections – 1300 K), the complex fuel particles absorb internal energy by means of rotations and vibrations that cause their specific heats to vary from those of diatomic molecules and noble gases. At more than double that temperature, electronic excitation and dissociation of the gas particles begins to occur causing the pressure to adjust to a greater number of particles (transition from gas to plasma). Finally, all of the thermodynamic processes were presumed to describe uniform gases whose velocities varied according to a fixed distribution. Using a non-equilibrium situation implies the flow field must be characterized in some manner to enable a solution. One of the first attempts to expand the boundaries of the ideal gas law was to include coverage for different thermodynamic processes by adjusting the equation to read ''pVn = constant'' and then varying the ''n'' through different values such as the specific heat ratio, ''γ''.
Real gas effects include those adjustments made to account for a greater range of gas behavior:
* Compressibility effects (''Z'' allowed to vary from 1.0)
*Variable heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity is a ...
(specific heats vary with temperature)
*Van der Waals forces (related to compressibility, can substitute other equations of state)
* Non-equilibrium thermodynamic effects
*Issues with molecular dissociation and elementary reaction
An elementary reaction is a chemical reaction in which one or more chemical species react directly to form Product (chemistry), products in a single reaction step and with a single transition state. In practice, a reaction is assumed to be element ...
s with variable composition.
For most applications, such a detailed analysis is excessive. Examples where real gas effects would have a significant impact would be on the Space Shuttle
The Space Shuttle is a retired, partially reusable launch system, reusable low Earth orbital spacecraft system operated from 1981 to 2011 by the U.S. National Aeronautics and Space Administration (NASA) as part of the Space Shuttle program. ...
re-entry where extremely high temperatures and pressures were present or the gases produced during geological events as in the image of the 1990 eruption of Mount Redoubt.
Permanent gas
Permanent gas is a term used for a gas which has a critical temperature below the range of normal human-habitable temperatures and therefore cannot be liquefied by pressure within this range. Historically such gases were thought to be impossible to liquefy and would therefore permanently remain in the gaseous state. The term is relevant to ambient temperature storage and transport of gases at high pressure.Historical research
Boyle's law
 Boyle's law was perhaps the first expression of an equation of state. In 1662 Robert Boyle performed a series of experiments employing a J-shaped glass tube, which was sealed on one end. Mercury was added to the tube, trapping a fixed quantity of air in the short, sealed end of the tube. Then the volume of gas was carefully measured as additional mercury was added to the tube. The pressure of the gas could be determined by the difference between the mercury level in the short end of the tube and that in the long, open end. The image of Boyle's equipment shows some of the exotic tools used by Boyle during his study of gases.
Through these experiments, Boyle noted that the pressure exerted by a gas held at a constant temperature varies inversely with the volume of the gas. For example, if the volume is halved, the pressure is doubled; and if the volume is doubled, the pressure is halved. Given the inverse relationship between pressure and volume, the product of pressure (''P'') and volume (''V'') is a constant (''k'') for a given mass of confined gas as long as the temperature is constant. Stated as a formula, thus is:
:
Because the before and after volumes and pressures of the fixed amount of gas, where the before and after temperatures are the same both equal the constant ''k'', they can be related by the equation:
Boyle's law was perhaps the first expression of an equation of state. In 1662 Robert Boyle performed a series of experiments employing a J-shaped glass tube, which was sealed on one end. Mercury was added to the tube, trapping a fixed quantity of air in the short, sealed end of the tube. Then the volume of gas was carefully measured as additional mercury was added to the tube. The pressure of the gas could be determined by the difference between the mercury level in the short end of the tube and that in the long, open end. The image of Boyle's equipment shows some of the exotic tools used by Boyle during his study of gases.
Through these experiments, Boyle noted that the pressure exerted by a gas held at a constant temperature varies inversely with the volume of the gas. For example, if the volume is halved, the pressure is doubled; and if the volume is doubled, the pressure is halved. Given the inverse relationship between pressure and volume, the product of pressure (''P'') and volume (''V'') is a constant (''k'') for a given mass of confined gas as long as the temperature is constant. Stated as a formula, thus is:
:
Because the before and after volumes and pressures of the fixed amount of gas, where the before and after temperatures are the same both equal the constant ''k'', they can be related by the equation:
Charles's law
In 1787, the French physicist and balloon pioneer, Jacques Charles, found that oxygen, nitrogen, hydrogen, carbon dioxide, and air expand to the same extent over the same 80 kelvin interval. He noted that, for an ideal gas at constant pressure, the volume is directly proportional to its temperature: :Gay-Lussac's law
In 1802, Joseph Louis Gay-Lussac published results of similar, though more extensive experiments. Gay-Lussac credited Charles' earlier work by naming the law in his honor. Gay-Lussac himself is credited with the law describing pressure, which he found in 1809. It states that the pressure exerted on a container's sides by an ideal gas is proportional to its temperature. :Avogadro's law
In 1811, Amedeo Avogadro verified that equal volumes of pure gases contain the same number of particles. His theory was not generally accepted until 1858 when another Italian chemist Stanislao Cannizzaro was able to explain non-ideal exceptions. For his work with gases a century prior, the physical constant that bears his name (theAvogadro constant
The Avogadro constant, commonly denoted or , is an SI defining constant with an exact value of when expressed in reciprocal moles.
It defines the ratio of the number of constituent particles to the amount of substance in a sample, where th ...
) is the number of atoms per mole of elemental carbon-12 (). This specific number of gas particles, at standard temperature and pressure (ideal gas law) occupies 22.40 liters, which is referred to as the molar volume
In chemistry and related fields, the molar volume, symbol ''V''m, or \tilde V of a substance is the ratio of the volume (''V'') occupied by a substance to the amount of substance (''n''), usually at a given temperature and pressure. It is also eq ...
.
Avogadro's law states that the volume occupied by an ideal gas is proportional to the amount of substance
In chemistry, the amount of substance (symbol ) in a given sample of matter is defined as a ratio () between the particle number, number of elementary entities () and the Avogadro constant (). The unit of amount of substance in the International ...
in the volume. This gives rise to the molar volume
In chemistry and related fields, the molar volume, symbol ''V''m, or \tilde V of a substance is the ratio of the volume (''V'') occupied by a substance to the amount of substance (''n''), usually at a given temperature and pressure. It is also eq ...
of a gas, which at STP is 22.4 dm3/mol (liters per mole). The relation is given by
where ''n'' is the amount of substance of gas (the number of molecules divided by the Avogadro constant
The Avogadro constant, commonly denoted or , is an SI defining constant with an exact value of when expressed in reciprocal moles.
It defines the ratio of the number of constituent particles to the amount of substance in a sample, where th ...
).
Dalton's law
 In 1801,
In 1801, John Dalton
John Dalton (; 5 or 6 September 1766 – 27 July 1844) was an English chemist, physicist and meteorologist. He introduced the atomic theory into chemistry. He also researched Color blindness, colour blindness; as a result, the umbrella term ...
published the law of partial pressures from his work with ideal gas law relationship: The pressure of a mixture of non reactive gases is equal to the sum of the pressures of all of the constituent gases alone. Mathematically, this can be represented for ''n'' species as:
: Pressuretotal = Pressure1 + Pressure2 + ... + Pressure''n''
The image of Dalton's journal depicts symbology he used as shorthand to record the path he followed. Among his key journal observations upon mixing unreactive "elastic fluids" (gases) were the following:
*Unlike liquids, heavier gases did not drift to the bottom upon mixing.
*Gas particle identity played no role in determining final pressure (they behaved as if their size was negligible).
Special topics
Compressibility
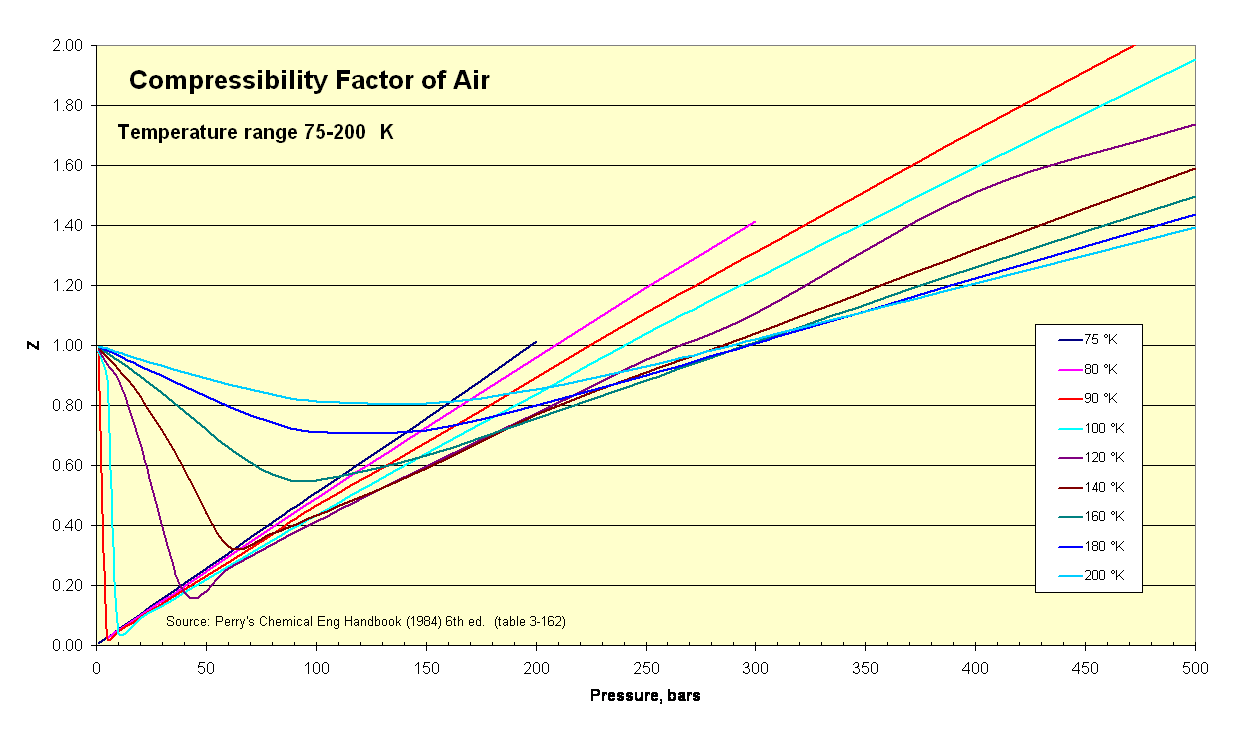
 Thermodynamicists use this factor (''Z'') to alter the ideal gas equation to account for compressibility effects of real gases. This factor represents the ratio of actual to ideal specific volumes. It is sometimes referred to as a "fudge-factor" or correction to expand the useful range of the ideal gas law for design purposes. ''Usually'' this ''Z'' value is very close to unity. The compressibility factor image illustrates how Z varies over a range of very cold temperatures.
Thermodynamicists use this factor (''Z'') to alter the ideal gas equation to account for compressibility effects of real gases. This factor represents the ratio of actual to ideal specific volumes. It is sometimes referred to as a "fudge-factor" or correction to expand the useful range of the ideal gas law for design purposes. ''Usually'' this ''Z'' value is very close to unity. The compressibility factor image illustrates how Z varies over a range of very cold temperatures.
Boundary layer
 Particles will, in effect, "stick" to the surface of an object moving through it. This layer of particles is called the boundary layer. At the surface of the object, it is essentially static due to the friction of the surface. The object, with its boundary layer is effectively the new shape of the object that the rest of the molecules "see" as the object approaches. This boundary layer can separate from the surface, essentially creating a new surface and completely changing the flow path. The classical example of this is a stalling airfoil. The delta wing image clearly shows the boundary layer thickening as the gas flows from right to left along the leading edge.
Particles will, in effect, "stick" to the surface of an object moving through it. This layer of particles is called the boundary layer. At the surface of the object, it is essentially static due to the friction of the surface. The object, with its boundary layer is effectively the new shape of the object that the rest of the molecules "see" as the object approaches. This boundary layer can separate from the surface, essentially creating a new surface and completely changing the flow path. The classical example of this is a stalling airfoil. The delta wing image clearly shows the boundary layer thickening as the gas flows from right to left along the leading edge.
Turbulence
 In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic, stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time. The satellite view of weather around Robinson Crusoe Islands illustrates one example.
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic, stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time. The satellite view of weather around Robinson Crusoe Islands illustrates one example.
Viscosity
Viscosity, a physical property, is a measure of how well adjacent molecules stick to one another. A solid can withstand a shearing force due to the strength of these sticky intermolecular forces. A fluid will continuously deform when subjected to a similar load. While a gas has a lower value of viscosity than a liquid, it is still an observable property. If gases had no viscosity, then they would not stick to the surface of a wing and form a boundary layer. A study of the delta wing in the Schlieren image reveals that the gas particles stick to one another (see Boundary layer section).Reynolds number
In fluid mechanics, the Reynolds number is the ratio of inertial forces (''vsρ'') which dominate a turbulent flow, to viscous forces (''μ/L'') which is proportional to viscosity. It is one of the most important dimensionless numbers in fluid dynamics and is used, usually along with other dimensionless numbers, to provide a criterion for determining dynamic similitude. As such, the Reynolds number provides the link between modeling results (design) and the full-scale actual conditions. It can also be used to characterize the flow.Maximum entropy principle
As the total number of degrees of freedom approaches infinity, the system will be found in themacrostate
In statistical mechanics, a microstate is a specific configuration of a system that describes the precise positions and momenta of all the individual particles or components that make up the system. Each microstate has a certain probability of ...
that corresponds to the highest multiplicity. In order to illustrate this principle, observe the skin temperature of a frozen metal bar. Using a thermal image of the skin temperature, note the temperature distribution on the surface. This initial observation of temperature represents a " microstate". At some future time, a second observation of the skin temperature produces a second microstate. By continuing this observation process, it is possible to produce a series of microstates that illustrate the thermal history of the bar's surface. Characterization of this historical series of microstates is possible by choosing the macrostate that successfully classifies them all into a single grouping.
Thermodynamic equilibrium
When energy transfer ceases from a system, this condition is referred to as thermodynamic equilibrium. Usually, this condition implies the system and surroundings are at the same temperature so that heat no longer transfers between them. It also implies that external forces are balanced (volume does not change), and all chemical reactions within the system are complete. The timeline varies for these events depending on the system in question. A container of ice allowed to melt at room temperature takes hours, while in semiconductors the heat transfer that occurs in the device transition from an on to off state could be on the order of a few nanoseconds.See also
*Greenhouse gas
Greenhouse gases (GHGs) are the gases in the atmosphere that raise the surface temperature of planets such as the Earth. Unlike other gases, greenhouse gases absorb the radiations that a planet emits, resulting in the greenhouse effect. T ...
* Landfill gas utilization
* List of gases
*Natural gas
Natural gas (also fossil gas, methane gas, and gas) is a naturally occurring compound of gaseous hydrocarbons, primarily methane (95%), small amounts of higher alkanes, and traces of carbon dioxide and nitrogen, hydrogen sulfide and helium ...
*Volcanic gas
Volcanic gases are gases given off by active (or, at times, by dormant) volcanoes. These include gases trapped in cavities (Vesicular texture, vesicles) in volcanic rocks, dissolved or dissociated gases in magma and lava, or gases emanating from ...
* Breathing gas
*Wind
Wind is the natural movement of atmosphere of Earth, air or other gases relative to a planetary surface, planet's surface. Winds occur on a range of scales, from thunderstorm flows lasting tens of minutes, to local breezes generated by heatin ...
Notes
References
* * *Further reading
*Philip Hill and Carl Peterson. ''Mechanics and Thermodynamics of Propulsion: Second Edition'' Addison-Wesley, 1992. *National Aeronautics and Space Administration (NASA)Animated Gas Lab
Accessed February 2008. *Georgia State University
Accessed February 2008. *Antony Lewi
WordWeb
Accessed February 2008. *Northwestern Michigan Colleg
Accessed February 2008. * {{Authority control Gases *Gas Articles containing video clips