Fixed-point iteration on:
[Wikipedia]
[Google]
[Amazon]
In
 * The fixed-point iteration converges to the unique fixed point of the function for any starting point This example does satisfy (at the latest after the first iteration step) the assumptions of the
* The fixed-point iteration converges to the unique fixed point of the function for any starting point This example does satisfy (at the latest after the first iteration step) the assumptions of the
 An ''attracting fixed point'' of a function ''f'' is a fixed point ''x''fix of ''f'' such that for any value of ''x'' in the domain that is close enough to ''x''fix, the fixed-point iteration sequence
:
converges to ''x''fix.
The natural cosine function ("natural" means in
An ''attracting fixed point'' of a function ''f'' is a fixed point ''x''fix of ''f'' such that for any value of ''x'' in the domain that is close enough to ''x''fix, the fixed-point iteration sequence
:
converges to ''x''fix.
The natural cosine function ("natural" means in
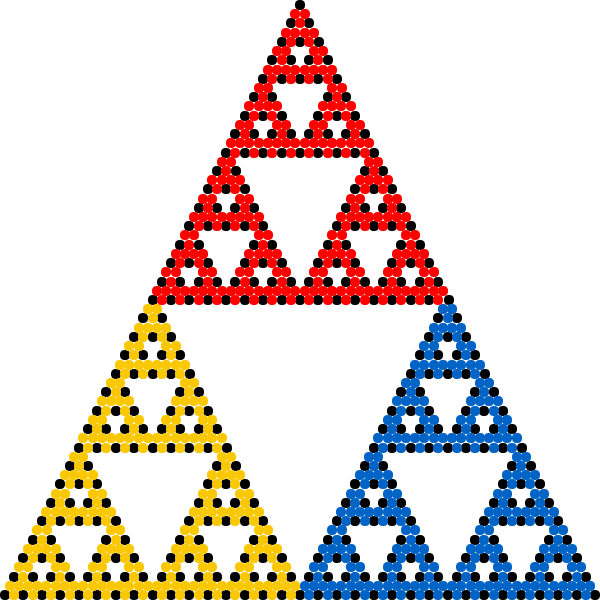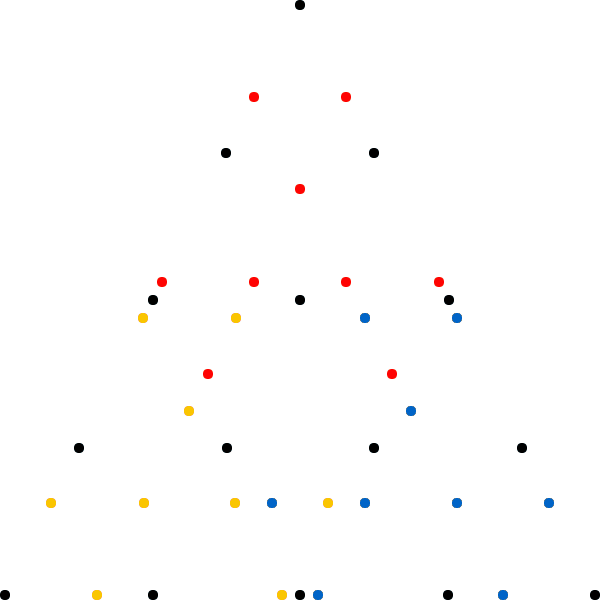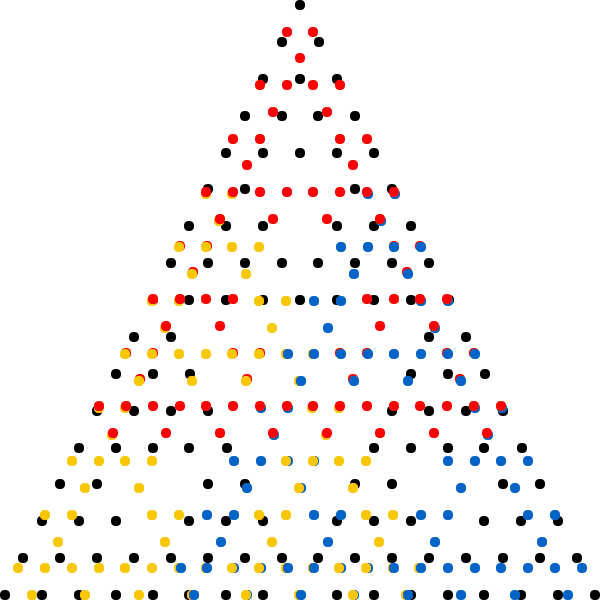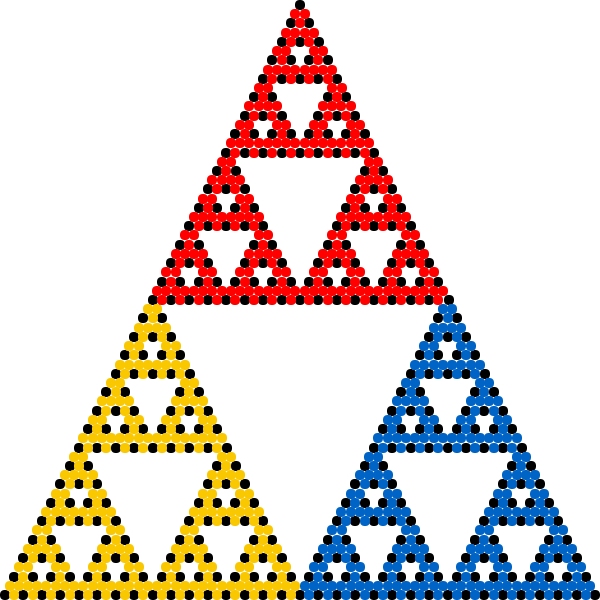 The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point ''x''0, successive iterations are formed as ''x''''k''+1 = ''f''''r''(''x''''k''), where ''f''''r'' is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a fractal such as the Sierpinski triangle by repeating the iterative process a large number of times. More mathematically, the iterations converge to the fixed point of the IFS. Whenever ''x''0 belongs to the attractor of the IFS, all iterations ''x''''k'' stay inside the attractor and, with probability 1, form a
The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point ''x''0, successive iterations are formed as ''x''''k''+1 = ''f''''r''(''x''''k''), where ''f''''r'' is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a fractal such as the Sierpinski triangle by repeating the iterative process a large number of times. More mathematically, the iterations converge to the fixed point of the IFS. Whenever ''x''0 belongs to the attractor of the IFS, all iterations ''x''''k'' stay inside the attractor and, with probability 1, form a
Fixed-point algorithms onlineFixed-point iteration online calculator (Mathematical Assistant on Web)
{{DEFAULTSORT:Fixed-Point Iteration Root-finding algorithms Iterative methods
numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods ...
, fixed-point iteration is a method of computing fixed points of a function.
More specifically, given a function defined on the real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s with real values and given a point in the domain of , the fixed-point iteration is
:
which gives rise to the sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is calle ...
of iterated function
In mathematics, an iterated function is a function (that is, a function from some set to itself) which is obtained by composing another function with itself a certain number of times. The process of repeatedly applying the same function is ...
applications which is hoped to converge
Converge may refer to:
* Converge (band), American hardcore punk band
* Converge (Baptist denomination), American national evangelical Baptist body
* Limit (mathematics)
* Converge ICT, internet service provider in the Philippines
*CONVERGE CFD s ...
to a point . If is continuous, then one can prove that the obtained is a fixed point of , i.e.,
:
More generally, the function can be defined on any metric space
In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general set ...
with values in that same space.
Examples
* A first simple and useful example is the Babylonian method for computing thesquare root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
of ''a''>0, which consists in taking , i.e. the mean value of ''x'' and ''a/x'', to approach the limit (from whatever starting point ). This is a special case of Newton's method quoted below.
Banach fixed-point theorem
In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem) is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certa ...
. Hence, the error after n steps satisfies (where we can take , if we start from .) When the error is less than a multiple of for some constant ''q'', we say that we have linear convergence
In numerical analysis, the order of convergence and the rate of convergence of a convergent sequence are quantities that represent how quickly the sequence approaches its limit. A sequence (x_n) that converges to x^* is said to have ''order of co ...
. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
* The requirement that ''f'' is continuous is important, as the following example shows. The iteration converges to 0 for all values of . However, 0 is ''not'' a fixed point of the function as this function is ''not'' continuous at , and in fact has no fixed points.
Attracting fixed points
radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s, not degrees or other units) has exactly one fixed point, and that fixed point is attracting. In this case, "close enough" is not a stringent criterion at all—to demonstrate this, start with ''any'' real number and repeatedly press the ''cos'' key on a calculator (checking first that the calculator is in "radians" mode). It eventually converges to the Dottie number
The Dottie number is the unique real fixed point of the cosine function.
In mathematics, the Dottie number is a constant that is the unique real root of the equation
: \cos x = x ,
where the argument of \cos is in radians. The decimal expan ...
(about 0.739085133), which is a fixed point. That is where the graph of the cosine function intersects the line .
Not all fixed points are attracting. For example, 0 is a fixed point of the function ''f''(''x'') = 2''x'', but iteration of this function for any value other than zero rapidly diverges. We say that the fixed point of is repelling.
An attracting fixed point is said to be a ''stable fixed point'' if it is also Lyapunov stable
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. T ...
.
A fixed point is said to be a ''neutrally stable fixed point'' if it is Lyapunov stable
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. T ...
but not attracting. The center of a linear homogeneous differential equation of the second order is an example of a neutrally stable fixed point.
Multiple attracting points can be collected in an ''attracting fixed set''.
Banach fixed-point theorem
TheBanach fixed-point theorem
In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem) is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certa ...
gives a sufficient condition for the existence of attracting fixed points. A contraction mapping In mathematics, a contraction mapping, or contraction or contractor, on a metric space (''M'', ''d'') is a function ''f'' from ''M'' to itself, with the property that there is some real number 0 \leq k < 1 such that for all ''x'' and ...
function defined on a complete metric space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in .
Intuitively, a space is complete if there are no "points missing" from it (inside or at the bou ...
has precisely one fixed point, and the fixed-point iteration is attracted towards that fixed point for any initial guess in the domain of the function. Common special cases are that (1) is defined on the real line with real values and is Lipschitz continuous
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there e ...
with Lipschitz constant , and (2) the function ''f'' is continuously differentiable in an open neighbourhood of a fixed point ''x''fix, and .
Although there are other fixed-point theorems
In mathematics, a fixed-point theorem is a result saying that a function ''F'' will have at least one fixed point (a point ''x'' for which ''F''(''x'') = ''x''), under some conditions on ''F'' that can be stated in general terms. Some authors cla ...
, this one in particular is very useful because not all fixed-points are attractive. When constructing a fixed-point iteration, it is very important to make sure it converges to the fixed point. We can usually use the Banach fixed-point theorem to show that the fixed point is attractive.
Attractors
Attracting fixed points are a special case of a wider mathematical concept ofattractor
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain ...
s. Fixed-point iterations are a discrete dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in ...
on one variable. Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. ...
studies dynamical systems and classifies various behaviors such as attracting fixed points, periodic orbits
In mathematics, specifically in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. It can be understood as the subset of phase space covered by the trajectory of the dynami ...
, or strange attractors. An example system is the logistic map.
Iterative methods
In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the n-th approximation is derived from the previous ones. Convergent fixed-point iterations are mathematically rigorous formalizations of iterative methods.Iterative method examples
Convergence acceleration
The speed of convergence of the iteration sequence can be increased by using a convergence acceleration method such as Anderson acceleration andAitken's delta-squared process
In numerical analysis, Aitken's delta-squared process or Aitken extrapolation is a series acceleration method, used for accelerating the rate of convergence of a sequence. It is named after Alexander Aitken, who introduced this method in 1926.Alexa ...
. The application of Aitken's method to fixed-point iteration is known as Steffensen's method, and it can be shown that Steffensen's method yields a rate of convergence that is at least quadratic.
Chaos game
 The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point ''x''0, successive iterations are formed as ''x''''k''+1 = ''f''''r''(''x''''k''), where ''f''''r'' is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a fractal such as the Sierpinski triangle by repeating the iterative process a large number of times. More mathematically, the iterations converge to the fixed point of the IFS. Whenever ''x''0 belongs to the attractor of the IFS, all iterations ''x''''k'' stay inside the attractor and, with probability 1, form a
The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point ''x''0, successive iterations are formed as ''x''''k''+1 = ''f''''r''(''x''''k''), where ''f''''r'' is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a fractal such as the Sierpinski triangle by repeating the iterative process a large number of times. More mathematically, the iterations converge to the fixed point of the IFS. Whenever ''x''0 belongs to the attractor of the IFS, all iterations ''x''''k'' stay inside the attractor and, with probability 1, form a dense set
In topology and related areas of mathematics, a subset ''A'' of a topological space ''X'' is said to be dense in ''X'' if every point of ''X'' either belongs to ''A'' or else is arbitrarily "close" to a member of ''A'' — for instance, the ra ...
in the latter.
See also
* Fixed-point combinator * Cobweb plot * Markov chain *Infinite compositions of analytic functions
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the ...
* Convergence and fixed point
References
Further reading
* * * * * *External links
Fixed-point algorithms online
{{DEFAULTSORT:Fixed-Point Iteration Root-finding algorithms Iterative methods