Extrinsic Curvature on:
[Wikipedia]
[Google]
[Amazon]
In
 Historically, the curvature of a differentiable curve was defined through the
Historically, the curvature of a differentiable curve was defined through the
 The expression of the curvature In terms of arc-length parametrization is essentially the first Frenet–Serret formula
:
where the primes refer to the derivatives with respect to the arc length , and is the normal unit vector in the direction of .
As planar curves have zero torsion, the second Frenet–Serret formula provides the relation
:
For a general parametrization by a parameter , one needs expressions involving derivatives with respect to . As these are obtained by multiplying by the derivatives with respect to , one has, for any proper parametrization
:
The expression of the curvature In terms of arc-length parametrization is essentially the first Frenet–Serret formula
:
where the primes refer to the derivatives with respect to the arc length , and is the normal unit vector in the direction of .
As planar curves have zero torsion, the second Frenet–Serret formula provides the relation
:
For a general parametrization by a parameter , one needs expressions involving derivatives with respect to . As these are obtained by multiplying by the derivatives with respect to , one has, for any proper parametrization
:
 A ''curvature comb'' can be used to represent graphically the curvature of every point on a curve. If is a parametrised curve its comb is defined as the parametrized curve
:
where are the curvature and normal vector and is a scaling factor (to be chosen as to enhance the graphical representation).
A ''curvature comb'' can be used to represent graphically the curvature of every point on a curve. If is a parametrised curve its comb is defined as the parametrized curve
:
where are the curvature and normal vector and is a scaling factor (to be chosen as to enhance the graphical representation).
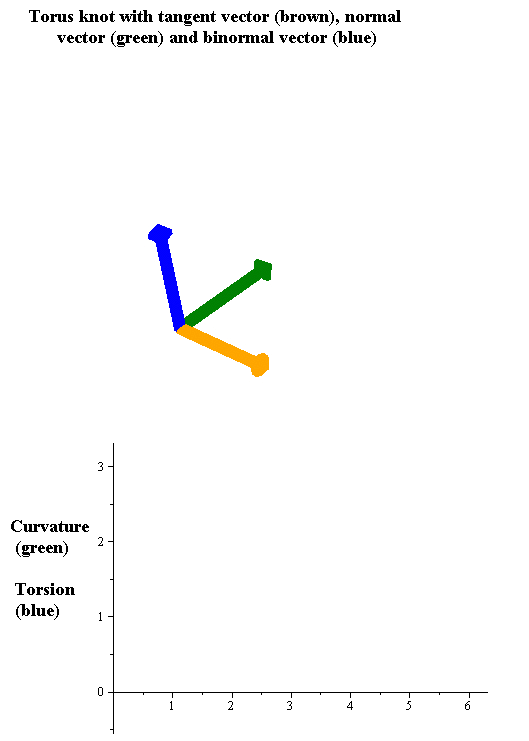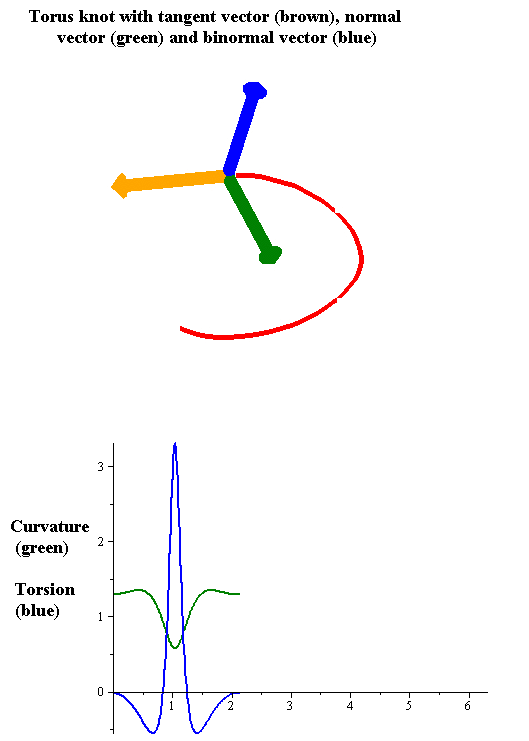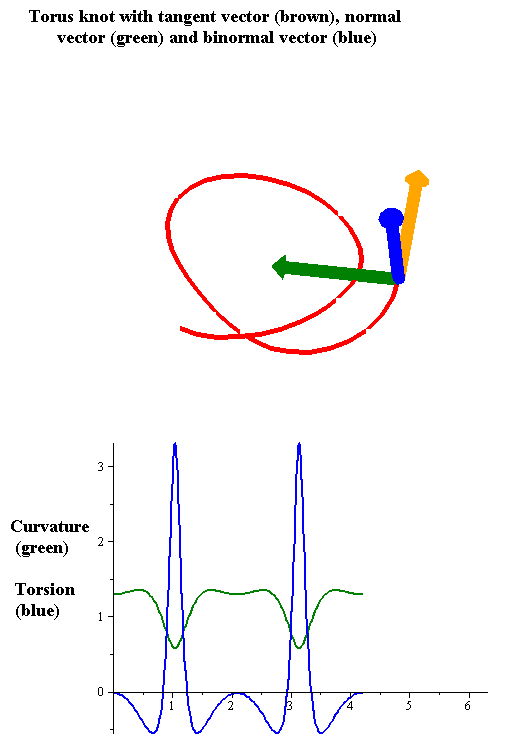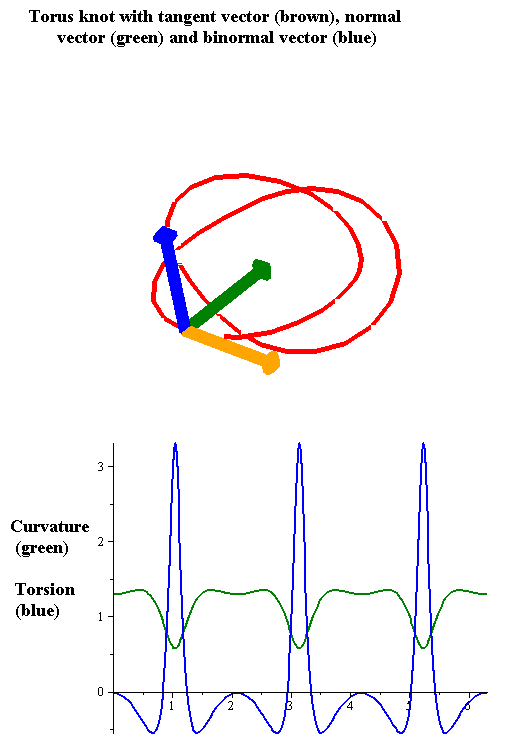 As in the case of curves in two dimensions, the curvature of a regular
As in the case of curves in two dimensions, the curvature of a regular
 All curves on the surface with the same tangent vector at a given point will have the same normal curvature, which is the same as the curvature of the curve obtained by intersecting the surface with the plane containing and . Taking all possible tangent vectors, the maximum and minimum values of the normal curvature at a point are called the principal curvatures, and , and the directions of the corresponding tangent vectors are called principal normal directions.
All curves on the surface with the same tangent vector at a given point will have the same normal curvature, which is the same as the curvature of the curve obtained by intersecting the surface with the plane containing and . Taking all possible tangent vectors, the maximum and minimum values of the normal curvature at a point are called the principal curvatures, and , and the directions of the corresponding tangent vectors are called principal normal directions.
 The mathematical notion of ''curvature'' is also defined in much more general contexts. Many of these generalizations emphasize different aspects of the curvature as it is understood in lower dimensions.
One such generalization is kinematic. The curvature of a curve can naturally be considered as a kinematic quantity, representing the force felt by a certain observer moving along the curve; analogously, curvature in higher dimensions can be regarded as a kind of
The mathematical notion of ''curvature'' is also defined in much more general contexts. Many of these generalizations emphasize different aspects of the curvature as it is understood in lower dimensions.
One such generalization is kinematic. The curvature of a curve can naturally be considered as a kinematic quantity, representing the force felt by a certain observer moving along the curve; analogously, curvature in higher dimensions can be regarded as a kind of
The Feynman Lectures on Physics Vol. II Ch. 42: Curved Space
at MathPages {{Authority control Multivariable calculus Articles containing video clips
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, curvature is any of several strongly related concepts in geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
. Intuitively, the curvature is the amount by which a curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
deviates from being a straight line
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segmen ...
, or a surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
deviates from being a plane.
For curves, the canonical example is that of a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
, which has a curvature equal to the reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
of its radius
In classical geometry, a radius (plural, : radii) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', ...
. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve i ...
, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
.
For surfaces (and, more generally for higher-dimensional manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a n ...
s), that are embedded in a Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or manifold. This leads to the concepts of ''maximal curvature'', ''minimal curvature'', and ''mean curvature''.
For Riemannian manifold
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g'p'' on the tangent space ...
s (of dimension at least two) that are not necessarily embedded in a Euclidean space, one can define the curvature ''intrinsically'', that is without referring to an external space. See Curvature of Riemannian manifolds for the definition, which is done in terms of lengths of curves traced on the manifold, and expressed, using linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as:
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as:
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrice ...
, by the Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. ...
.
History
In ''Tractatus de configurationibus qualitatum et motuum,'' the 14th-century philosopher and mathematicianNicole Oresme
Nicole Oresme (; c. 1320–1325 – 11 July 1382), also known as Nicolas Oresme, Nicholas Oresme, or Nicolas d'Oresme, was a French philosopher of the later Middle Ages. He wrote influential works on economics, mathematics, physics, astrology an ...
introduces the concept of curvature as a measure of departure from straightness; for circles he has the curvature as being inversely proportional to the radius; and he attempts to extend this idea to other curves as a continuously varying magnitude.
The curvature of a differentiable curve was originally defined through osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve i ...
s. In this setting, Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. H ...
showed that the center of curvature is the intersection point of two infinitely close normal lines to the curve.
Plane curves
Intuitively, the curvature describes for any part of a curve how much the curve direction changes over a small distance travelled (e.g. angle in ), so it is a measure of theinstantaneous rate of change
In physics and the philosophy of science, instant refers to an infinitesimal interval in time, whose passage is instantaneous. In ordinary speech, an instant has been defined as "a point or very short space of time," a notion deriving from its ...
of ''direction'' of a point that moves on the curve: the larger the curvature, the larger this rate of change. In other words, the curvature measures how fast the unit tangent vector to the curve rotates (fast in terms of curve position). In fact, it can be proved that this instantaneous rate of change is exactly the curvature. More precisely, suppose that the point is moving on the curve at a constant speed of one unit, that is, the position of the point is a function of the parameter , which may be thought as the time or as the arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
from a given origin. Let be a unit tangent vector
Unit may refer to:
Arts and entertainment
* UNIT, a fictional military organization in the science fiction television series ''Doctor Who''
* Unit of action, a discrete piece of action (or beat) in a theatrical presentation
Music
* ''Unit'' (al ...
of the curve at , which is also the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
of with respect to . Then, the derivative of with respect to is a vector that is normal to the curve and whose length is the curvature.
For being meaningful, the definition of the curvature and its different characterizations require that the curve is continuously differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
near , for having a tangent that varies continuously; it requires also that the curve is twice differentiable at , for insuring the existence of the involved limits, and of the derivative of .
The characterization of the curvature in terms of the derivative of the unit tangent vector is probably less intuitive than the definition in terms of the osculating circle, but formulas for computing the curvature are easier to deduce. Therefore, and also because of its use in kinematics
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move. Kinematics, as a fiel ...
, this characterization is often given as a definition of the curvature.
Osculating circle
osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve i ...
, which is the circle that best approximates the curve at a point. More precisely, given a point on a curve, every other point of the curve defines a circle (or sometimes a line) passing through and tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
to the curve at . The osculating circle is the limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
, if it exists, of this circle when tends to . Then the ''center'' and the ''radius of curvature'' of the curve at are the center and the radius of the osculating circle. The curvature is the reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
of radius of curvature. That is, the curvature is
:
where is the radius of curvature (the whole circle has this curvature, it can be read as turn over the length ).
This definition is difficult to manipulate and to express in formulas. Therefore, other equivalent definitions have been introduced.
In terms of arc-length parametrization
Every differentiable curve can be parametrized with respect toarc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
. In the case of a plane curve, this means the existence of a parametrization , where and are real-valued differentiable functions whose derivatives satisfy
:
This means that the tangent vector
:
has a norm equal to one and is thus a unit tangent vector
Unit may refer to:
Arts and entertainment
* UNIT, a fictional military organization in the science fiction television series ''Doctor Who''
* Unit of action, a discrete piece of action (or beat) in a theatrical presentation
Music
* ''Unit'' (al ...
.
If the curve is twice differentiable, that is, if the second derivatives of and exist, then the derivative of exists. This vector is normal to the curve, its norm is the curvature , and it is oriented toward the center of curvature. That is,
:
Moreover, as the radius of curvature is
:
and the center of curvature is on the normal to the curve, the center of curvature is the point
:
If is the unit normal vector obtained from by a counterclockwise rotation of , then
:
with . The real number is called the oriented curvature or signed curvature. It depends on both the orientation of the plane (definition of counterclockwise), and the orientation of the curve provided by the parametrization. In fact, the change of variable
Change or Changing may refer to:
Alteration
* Impermanence, a difference in a state of affairs at different points in time
* Menopause, also referred to as "the change", the permanent cessation of the menstrual period
* Metamorphosis, or change, ...
provides another arc-length parametrization, and changes the sign of .
In terms of a general parametrization
Let be a properparametric representation
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric o ...
of a twice differentiable plane curve. Here ''proper'' means that on the domain
Domain may refer to:
Mathematics
*Domain of a function, the set of input values for which the (total) function is defined
** Domain of definition of a partial function
** Natural domain of a partial function
**Domain of holomorphy of a function
* ...
of definition of the parametrization, the derivative
is defined, differentiable and nowhere equal to the zero vector.
With such a parametrization, the signed curvature is
:
where primes refer to derivatives with respect to . The curvature is thus
:
These can be expressed in a coordinate-free way as
:
These formulas can be derived from the special case of arc-length parametrization in the following way. The above condition on the parametrisation imply that the arc length is a differentiable monotonic function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
of the parameter , and conversely that is a monotonic function of . Moreover, by changing, if needed, to , one may suppose that these functions are increasing and have a positive derivative. Using notation of the preceding section and the chain rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , ...
, one has
:
and thus, by taking the norm of both sides
:
where the prime denotes differentiation with respect to .
The curvature is the norm of the derivative of with respect to .
By using the above formula and the chain rule this derivative and its norm can be expressed in terms of and only, with the arc-length parameter completely eliminated, giving the above formulas for the curvature.
Graph of a function
Thegraph of a function
In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subs ...
, is a special case of a parametrized curve, of the form
:
As the first and second derivatives of are 1 and 0, previous formulas simplify to
:
for the curvature, and to
:
for the signed curvature.
In the general case of a curve, the sign of the signed curvature is somewhat arbitrary, as it depends on the orientation of the curve. In the case of the graph of a function, there is a natural orientation by increasing values of . This makes significant the sign of the signed curvature.
The sign of the signed curvature is the same as the sign of the second derivative of . If it is positive then the graph has an upward concavity, and, if it is negative the graph has a downward concavity. It is zero, then one has an inflection point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case ...
or an undulation point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of ...
.
When the slope
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is use ...
of the graph (that is the derivative of the function) is small, the signed curvature is well approximated by the second derivative. More precisely, using big O notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund L ...
, one has
:
It is common in physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which ...
and engineering
Engineering is the use of scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more speciali ...
to approximate the curvature with the second derivative, for example, in beam theory
Beam may refer to:
Streams of particles or energy
*Light beam, or beam of light, a directional projection of light energy
**Laser beam
*Particle beam, a stream of charged or neutral particles
**Charged particle beam, a spatially localized grou ...
or for deriving the wave equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and ...
of a string under tension, and other applications where small slopes are involved. This often allows systems that are otherwise nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many oth ...
to be treated approximately as linear.
Polar coordinates
If a curve is defined inpolar coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to th ...
by the radius expressed as a function of the polar angle, that is is a function of , then its curvature is
:
where the prime refers to differentiation with respect to .
This results from the formula for general parametrizations, by considering the parametrization
:
Implicit curve
For a curve defined by animplicit equation
In mathematics, an implicit equation is a relation of the form R(x_1, \dots, x_n) = 0, where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is x^2 + y^2 - 1 = 0.
An implicit func ...
with partial derivatives
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Pa ...
denoted , , , , ,
the curvature is given by
:
The signed curvature is not defined, as it depends on an orientation of the curve that is not provided by the implicit equation. Also, changing into does not change the curve, but changes the sign of the numerator if the absolute value is omitted in the preceding formula.
A point of the curve where is a singular point
Singularity or singular point may refer to:
Science, technology, and mathematics Mathematics
* Mathematical singularity, a point at which a given mathematical object is not defined or not "well-behaved", for example infinite or not differentiab ...
, which means that the curve is not differentiable at this point, and thus that the curvature is not defined (most often, the point is either a crossing point or a cusp
A cusp is the most pointed end of a curve. It often refers to cusp (anatomy), a pointed structure on a tooth.
Cusp or CUSP may also refer to:
Mathematics
* Cusp (singularity), a singular point of a curve
* Cusp catastrophe, a branch of bifurc ...
).
Above formula for the curvature can be derived from the expression of the curvature of the graph of a function by using the implicit function theorem and the fact that, on such a curve, one has
:
Examples
It can be useful to verify on simple examples that the different formulas given in the preceding sections give the same result.Circle
A common parametrization of acircle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
of radius is . The formula for the curvature gives
:
It follows, as expected, that the radius of curvature is the radius of the circle, and that the center of curvature is the center of the circle.
The circle is a rare case where the arc-length parametrization is easy to compute, as it is
:
It is an arc-length parametrization, since the norm of
:
is equal to one. This parametrization gives the same value for the curvature, as it amounts to division by in both the numerator and the denominator in the preceding formula.
The same circle can also be defined by the implicit equation with . Then, the formula for the curvature in this case gives
:
Parabola
Consider theparabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descri ...
.
It is the graph of a function, with derivative , and second derivative . So, the signed curvature is
:
It has the sign of for all values of . This means that, if , the concavity is upward directed everywhere; if , the concavity is downward directed; for , the curvature is zero everywhere, confirming that the parabola degenerates into a line in this case.
The (unsigned) curvature is maximal for , that is at the stationary point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" in ...
(zero derivative) of the function, which is the vertex
Vertex, vertices or vertexes may refer to:
Science and technology Mathematics and computer science
*Vertex (geometry), a point where two or more curves, lines, or edges meet
*Vertex (computer graphics), a data structure that describes the position ...
of the parabola.
Consider the parametrization . The first derivative of is , and the second derivative is zero. Substituting into the formula for general parametrizations gives exactly the same result as above, with replaced by . If we use primes for derivatives with respect to the parameter .
The same parabola can also be defined by the implicit equation with . As , and , one obtains exactly the same value for the (unsigned) curvature. However, the signed curvature is meaningless here, as is a valid implicit equation for the same parabola, which gives the opposite sign for the curvature.
Frenet–Serret formulas for plane curves
Curvature comb
 A ''curvature comb'' can be used to represent graphically the curvature of every point on a curve. If is a parametrised curve its comb is defined as the parametrized curve
:
where are the curvature and normal vector and is a scaling factor (to be chosen as to enhance the graphical representation).
A ''curvature comb'' can be used to represent graphically the curvature of every point on a curve. If is a parametrised curve its comb is defined as the parametrized curve
:
where are the curvature and normal vector and is a scaling factor (to be chosen as to enhance the graphical representation).
Space curves
 As in the case of curves in two dimensions, the curvature of a regular
As in the case of curves in two dimensions, the curvature of a regular space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
in three dimensions (and higher) is the magnitude of the acceleration of a particle moving with unit speed along a curve. Thus if is the arc-length parametrization of then the unit tangent vector is given by
:
and the curvature is the magnitude of the acceleration:
:
The direction of the acceleration is the unit normal vector , which is defined by
:
The plane containing the two vectors and is the osculating plane {{Unreferenced, date=May 2019, bot=noref (GreenC bot)
In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a secon ...
to the curve at . The curvature has the following geometrical interpretation. There exists a circle in the osculating plane tangent to whose Taylor series to second order at the point of contact agrees with that of . This is the osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve i ...
to the curve. The radius of the circle is called the radius of curvature, and the curvature is the reciprocal of the radius of curvature:
:
The tangent, curvature, and normal vector together describe the second-order behavior of a curve near a point. In three dimensions, the third-order behavior of a curve is described by a related notion of torsion, which measures the extent to which a curve tends to move as a helical path in space. The torsion and curvature are related by the Frenet–Serret formulas
In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a differentiable curve in three-dimensional Euclidean space \mathbb^, or the geometric properties of the curve itself irrespective ...
(in three dimensions) and their generalization (in higher dimensions).
General expressions
For a parametrically-defined space curve in three dimensions given in Cartesian coordinates by , the curvature is : where the prime denotes differentiation with respect to the parameter . This can be expressed independently of the coordinate system by means of the formula : where × denotes the vector cross product. This last formula is valid for the curvature of curves in a Euclidean space of any dimension: :Curvature from arc and chord length
Given two points and on , let be the arc length of the portion of the curve between and and let denote the length of the line segment from to . The curvature of at is given by the limit : where the limit is taken as the point approaches on . The denominator can equally well be taken to be . The formula is valid in any dimension. Furthermore, by considering the limit independently on either side of , this definition of the curvature can sometimes accommodate a singularity at . The formula follows by verifying it for the osculating circle.Surfaces
The curvature of curves drawn on asurface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
is the main tool for the defining and studying the curvature of the surface.
Curves on surfaces
For a curve drawn on a surface (embedded in three-dimensionalEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
), several curvatures are defined, which relates the direction of curvature to the surface's unit normal vector
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve ...
, including the:
* normal curvature In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non- umbilic point of ...
*geodesic curvature In Riemannian geometry, the geodesic curvature k_g of a curve \gamma measures how far the curve is from being a geodesic. For example, for 1D curves on a 2D surface embedded in 3D space, it is the curvature of the curve projected onto the surface's ...
*geodesic torsion In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a s ...
Any non-singular curve on a smooth surface has its tangent vector contained in the tangent plane of the surface. The normal curvature, , is the curvature of the curve projected onto the plane containing the curve's tangent and the surface normal ; the geodesic curvature, , is the curvature of the curve projected onto the surface's tangent plane; and the geodesic torsion (or relative torsion), , measures the rate of change of the surface normal around the curve's tangent.
Let the curve be arc-length parametrized, and let so that form an orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space ''V'' with finite dimension is a basis for V whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other. For examp ...
, called the Darboux frame. The above quantities are related by:
:
Principal curvature
Normal sections
Curvature can be evaluated along surface normal sections, similar to above (see for example theEarth radius of curvature
Earth radius (denoted as ''R''🜨 or R_E) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly (equatorial radius, den ...
).
Developable surfaces
Some curved surfaces, such as those made from a smooth sheet of paper, can be flattened down into the plane without distorting their intrinsic features in any way. Such developable surfaces have zero Gaussian curvature (see below).Gaussian curvature
In contrast to curves, which do not have intrinsic curvature, but do have extrinsic curvature (they only have a curvature given an embedding), surfaces can have intrinsic curvature, independent of an embedding. TheGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a surface at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
The Gaussian radius of curvature is the reciprocal of .
...
, named after Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
, is equal to the product of the principal curvatures, . It has a dimension of length−2 and is positive for sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the c ...
s, negative for one-sheet hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by def ...
s and zero for planes and cylinders
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an in ...
. It determines whether a surface is locally convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
(when it is positive) or locally saddle-shaped (when it is negative).
Gaussian curvature is an ''intrinsic'' property of the surface, meaning it does not depend on the particular embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.
When some object X is said to be embedded in another object Y, the embedding is g ...
of the surface; intuitively, this means that ants living on the surface could determine the Gaussian curvature. For example, an ant living on a sphere could measure the sum of the interior angles of a triangle and determine that it was greater than 180 degrees, implying that the space it inhabited had positive curvature. On the other hand, an ant living on a cylinder would not detect any such departure from Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
; in particular the ant could not detect that the two surfaces have different mean curvatures (see below), which is a purely extrinsic type of curvature.
Formally, Gaussian curvature only depends on the Riemannian metric
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g'p'' on the tangent space '' ...
of the surface. This is Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
's celebrated Theorema Egregium, which he found while concerned with geographic surveys and mapmaking.
An intrinsic definition of the Gaussian curvature at a point is the following: imagine an ant which is tied to with a short thread of length . It runs around while the thread is completely stretched and measures the length of one complete trip around . If the surface were flat, the ant would find . On curved surfaces, the formula for will be different, and the Gaussian curvature at the point can be computed by the Bertrand–Diguet–Puiseux theorem
In the mathematics, mathematical study of the differential geometry of surfaces, the Bertrand–Diguet–Puiseux theorem expresses the Gaussian curvature of a surface in terms of the circumference of a geodesic circle, or the area of a geodesic dis ...
as
:
The integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
of the Gaussian curvature over the whole surface is closely related to the surface's Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological spac ...
; see the Gauss–Bonnet theorem.
The discrete analog of curvature, corresponding to curvature being concentrated at a point and particularly useful for polyhedra
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on ...
, is the (angular) defect; the analog for the Gauss–Bonnet theorem is Descartes' theorem on total angular defect.
Because (Gaussian) curvature can be defined without reference to an embedding space, it is not necessary that a surface be embedded in a higher-dimensional space in order to be curved. Such an intrinsically curved two-dimensional surface is a simple example of a Riemannian manifold
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g'p'' on the tangent space ...
.
Mean curvature
The mean curvature is an ''extrinsic'' measure of curvature equal to half the sum of theprincipal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how the surface bends b ...
s, . It has a dimension of length−1. Mean curvature is closely related to the first variation of surface area
The surface area of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of ...
. In particular, a minimal surface
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below).
The term "minimal surface" is used because these surfaces originally arose as surfaces tha ...
such as a soap film
Soap films are thin layers of liquid (usually water-based) surrounded by air. For example, if two soap bubbles come into contact, they merge and a thin film is created in between. Thus, foams are composed of a network of films connected by Platea ...
has mean curvature zero and a soap bubble
A soap bubble is an extremely thin film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds before bursting, either on their own or on contact wi ...
has constant mean curvature. Unlike Gauss curvature, the mean curvature is extrinsic and depends on the embedding, for instance, a cylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an ...
and a plane are locally isometric but the mean curvature of a plane is zero while that of a cylinder is nonzero.
Second fundamental form
The intrinsic and extrinsic curvature of a surface can be combined in the second fundamental form. This is aquadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial). For example,
:4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong to ...
in the tangent plane to the surface at a point whose value at a particular tangent vector to the surface is the normal component of the acceleration of a curve along the surface tangent to ; that is, it is the normal curvature to a curve tangent to (see above). Symbolically,
:
where is the unit normal to the surface. For unit tangent vectors , the second fundamental form assumes the maximum value and minimum value , which occur in the principal directions and , respectively. Thus, by the principal axis theorem
In the mathematical fields of geometry and linear algebra, a principal axis is a certain line in a Euclidean space associated with an ellipsoid or hyperboloid, generalizing the major and minor axes of an ellipse or hyperbola. The principal axis t ...
, the second fundamental form is
:
Thus the second fundamental form encodes both the intrinsic and extrinsic curvatures.
Shape operator
An encapsulation of surface curvature can be found in the shape operator, , which is aself-adjoint
In mathematics, and more specifically in abstract algebra, an element ''x'' of a *-algebra is self-adjoint if x^*=x. A self-adjoint element is also Hermitian, though the reverse doesn't necessarily hold.
A collection ''C'' of elements of a st ...
linear operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a Map (mathematics), mapping V \to W between two vect ...
from the tangent plane to itself (specifically, the differential of the Gauss map).
For a surface with tangent vectors and normal , the shape operator can be expressed compactly in index summation notation as
:
(Compare the alternative expression of curvature for a plane curve.)
The Weingarten equations The Weingarten equations give the expansion of the derivative of the unit normal vector to a surface in terms of the first derivatives of the position vector of a point on the surface. These formulas were established in 1861 by the German mathematic ...
give the value of in terms of the coefficients of the first and second fundamental forms as
:
The principal curvatures are the eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denote ...
of the shape operator, the principal curvature directions are its eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted ...
, the Gauss curvature is its determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if a ...
, and the mean curvature is half its trace.
Curvature of space
By extension of the former argument, a space of three or more dimensions can be intrinsically curved. The curvature is ''intrinsic'' in the sense that it is a property defined at every point in the space, rather than a property defined with respect to a larger space that contains it. In general, a curved space may or may not be conceived as being embedded in a higher-dimensional ambient space; if not then its curvature can only be defined intrinsically. After the discovery of the intrinsic definition of curvature, which is closely connected withnon-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean g ...
, many mathematicians and scientists questioned whether ordinary physical space might be curved, although the success of Euclidean geometry up to that time meant that the radius of curvature must be astronomically large. In the theory of general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
, which describes gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
and cosmology
Cosmology () is a branch of physics and metaphysics dealing with the nature of the universe. The term ''cosmology'' was first used in English in 1656 in Thomas Blount's ''Glossographia'', and in 1731 taken up in Latin by German philosopher ...
, the idea is slightly generalised to the "curvature of spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differ ...
"; in relativity theory spacetime is a pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the ...
. Once a time coordinate is defined, the three-dimensional space corresponding to a particular time is generally a curved Riemannian manifold; but since the time coordinate choice is largely arbitrary, it is the underlying spacetime curvature that is physically significant.
Although an arbitrarily curved space is very complex to describe, the curvature of a space which is locally isotropic
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describ ...
and homogeneous
Homogeneity and heterogeneity are concepts often used in the sciences and statistics relating to the uniformity of a substance or organism. A material or image that is homogeneous is uniform in composition or character (i.e. color, shape, siz ...
is described by a single Gaussian curvature, as for a surface; mathematically these are strong conditions, but they correspond to reasonable physical assumptions (all points and all directions are indistinguishable). A positive curvature corresponds to the inverse square radius of curvature; an example is a sphere or hypersphere
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, call ...
. An example of negatively curved space is hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
. A space or space-time with zero curvature is called flat. For example, Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
is an example of a flat space, and Minkowski space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the iner ...
is an example of a flat spacetime. There are other examples of flat geometries in both settings, though. A torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.
If the axis of revolution does n ...
or a cylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an ...
can both be given flat metrics, but differ in their topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ...
. Other topologies are also possible for curved space. See also shape of the universe
The shape of the universe, in physical cosmology, is the local and global geometry of the universe. The local features of the geometry of the universe are primarily described by its curvature, whereas the topology of the universe describes ge ...
.
Generalizations
tidal force
The tidal force is a gravitational effect that stretches a body along the line towards the center of mass of another body due to a gradient (difference in strength) in gravitational field from the other body; it is responsible for diverse phenomen ...
(this is one way of thinking of the sectional curvature In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature ''K''(σ''p'') depends on a two-dimensional linear subspace σ''p'' of the tangent space at a p ...
). This generalization of curvature depends on how nearby test particles diverge or converge when they are allowed to move freely in the space; see Jacobi field.
Another broad generalization of curvature comes from the study of parallel transport
In geometry, parallel transport (or parallel translation) is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection (a covariant derivative or connection on the tangent b ...
on a surface. For instance, if a vector is moved around a loop on the surface of a sphere keeping parallel throughout the motion, then the final position of the vector may not be the same as the initial position of the vector. This phenomenon is known as holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geomet ...
. Various generalizations capture in an abstract form this idea of curvature as a measure of holonomy; see curvature form. A closely related notion of curvature comes from gauge theory
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations ( Lie grou ...
in physics, where the curvature represents a field and a vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a ''scalar potential'', which is a scalar field whose gradient is a given vector field.
Formally, given a vector field v, a ''vecto ...
for the field is a quantity that is in general path-dependent: it may change if an observer moves around a loop.
Two more generalizations of curvature are the scalar curvature
In the mathematical field of Riemannian geometry, the scalar curvature (or the Ricci scalar) is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geome ...
and Ricci curvature. In a curved surface such as the sphere, the area of a disc on the surface differs from the area of a disc of the same radius in flat space. This difference (in a suitable limit) is measured by the scalar curvature. The difference in area of a sector of the disc is measured by the Ricci curvature. Each of the scalar curvature and Ricci curvature are defined in analogous ways in three and higher dimensions. They are particularly important in relativity theory, where they both appear on the side of Einstein's field equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Einstein in 1915 in the for ...
that represents the geometry of spacetime (the other side of which represents the presence of matter and energy). These generalizations of curvature underlie, for instance, the notion that curvature can be a property of a measure; see curvature of a measure
In mathematics, the curvature of a measure defined on the Euclidean plane R2 is a quantification of how much the measure's "distribution of mass" is "curved". It is related to notions of curvature in geometry. In the form presented below, the con ...
.
Another generalization of curvature relies on the ability to compare a curved space with another space that has ''constant'' curvature. Often this is done with triangles in the spaces. The notion of a triangle makes senses in metric space
In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setti ...
s, and this gives rise to spaces.
See also
* Curvature form for the appropriate notion of curvature forvector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every p ...
s and principal bundle
In mathematics, a principal bundle is a mathematical object that formalizes some of the essential features of the Cartesian product X \times G of a space X with a group G. In the same way as with the Cartesian product, a principal bundle P is equi ...
s with connection
* Curvature of a measure
In mathematics, the curvature of a measure defined on the Euclidean plane R2 is a quantification of how much the measure's "distribution of mass" is "curved". It is related to notions of curvature in geometry. In the form presented below, the con ...
for a notion of curvature in measure theory
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many simila ...
* Curvature of parametric surfaces
* Curvature of Riemannian manifolds for generalizations of Gauss curvature to higher-dimensional Riemannian manifold
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g'p'' on the tangent space ...
s
* Curvature vector and geodesic curvature In Riemannian geometry, the geodesic curvature k_g of a curve \gamma measures how far the curve is from being a geodesic. For example, for 1D curves on a 2D surface embedded in 3D space, it is the curvature of the curve projected onto the surface's ...
for appropriate notions of curvature of ''curves in'' Riemannian manifolds, of any dimension
* Degree of curvature
* Differential geometry of curves
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus.
Many specific curves have been thoroughly investigated using the ...
for a full treatment of curves embedded in a Euclidean space of arbitrary dimension
* Dioptre
A dioptre (British spelling) or diopter (American spelling) is a unit of measurement with dimension of reciprocal length, equivalent to one reciprocal metre, 1 dioptre = 1 m−1. It is normally used to express the optical power of a lens or ...
, a measurement of curvature used in optics
* Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the resultant shape will be the evolute of that cur ...
, the locus of the centers of curvature of a given curve
* Fundamental theorem of curves
* Gauss–Bonnet theorem for an elementary application of curvature
* Gauss map for more geometric properties of Gauss curvature
* Gauss's principle of least constraint, an expression of the Principle of Least Action
The stationary-action principle – also known as the principle of least action – is a variational principle that, when applied to the '' action'' of a mechanical system, yields the equations of motion for that system. The principle states tha ...
* Mean curvature at one point on a surface
* Minimum railway curve radius
The minimum railway curve radius is the shortest allowable design radius for the centerline of railway tracks under a particular set of conditions. It has an important bearing on construction costs and operating costs and, in combination with ...
* Radius of curvature
* Second fundamental form for the extrinsic curvature of hypersurfaces in general
* Sinuosity
Sinuosity, sinuosity index, or sinuosity coefficient of a continuously differentiable curve having at least one inflection point is the ratio of the curvilinear length (along the curve) and the Euclidean distance (straight line) between the en ...
* Torsion of a curve
Notes
References
* * * () * () *External links
The Feynman Lectures on Physics Vol. II Ch. 42: Curved Space
at MathPages {{Authority control Multivariable calculus Articles containing video clips