cubic polynomial on:
[Wikipedia]
[Google]
[Amazon]
In
 The graph of a cubic function is a cubic curve, though many cubic curves are not graphs of functions.
Although cubic functions depend on four parameters, their graph can have only very few shapes. In fact, the graph of a cubic function is always similar to the graph of a function of the form
:
This similarity can be built as the composition of
The graph of a cubic function is a cubic curve, though many cubic curves are not graphs of functions.
Although cubic functions depend on four parameters, their graph can have only very few shapes. In fact, the graph of a cubic function is always similar to the graph of a function of the form
:
This similarity can be built as the composition of
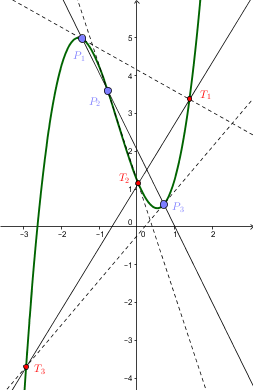 The tangent lines to the graph of a cubic function at three collinear points intercept the cubic again at collinear points. This can be seen as follows.
As this property is invariant under a rigid motion, one may suppose that the function has the form
:
If is a real number, then the tangent to the graph of at the point is the line
:.
So, the intersection point between this line and the graph of can be obtained solving the equation , that is
:
which can be rewritten
:
and factorized as
:
So, the tangent intercepts the cubic at
:
So, the function that maps a point of the graph to the other point where the tangent intercepts the graph is
:
This is an
The tangent lines to the graph of a cubic function at three collinear points intercept the cubic again at collinear points. This can be seen as follows.
As this property is invariant under a rigid motion, one may suppose that the function has the form
:
If is a real number, then the tangent to the graph of at the point is the line
:.
So, the intersection point between this line and the graph of can be obtained solving the equation , that is
:
which can be rewritten
:
and factorized as
:
So, the tangent intercepts the cubic at
:
So, the function that maps a point of the graph to the other point where the tangent intercepts the graph is
:
This is an
History of quadratic, cubic and quartic equations
on
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a cubic function is a function of the form
where the coefficients , , , and are complex numbers, and the variable takes real values, and . In other words, it is both a polynomial function
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An exa ...
of degree three, and a real function. In particular, the domain
Domain may refer to:
Mathematics
*Domain of a function, the set of input values for which the (total) function is defined
** Domain of definition of a partial function
** Natural domain of a partial function
**Domain of holomorphy of a function
* ...
and the codomain are the set of the real numbers.
Setting produces a cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of th ...
of the form
:
whose solutions are called roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
of the function.
A cubic function has either one or three real roots (which may not be distinct); all odd-degree polynomials have at least one real root.
The graph of a cubic function always has a single inflection point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case ...
. It may have two critical points, a local minimum and a local maximum. Otherwise, a cubic function is monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
. The graph of a cubic function is symmetric with respect to its inflection point; that is, it is invariant under a rotation of a half turn around this point. Up to Two mathematical objects ''a'' and ''b'' are called equal up to an equivalence relation ''R''
* if ''a'' and ''b'' are related by ''R'', that is,
* if ''aRb'' holds, that is,
* if the equivalence classes of ''a'' and ''b'' with respect to ''R'' ...
an affine transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More generall ...
, there are only three possible graphs for cubic functions.
Cubic functions are fundamental for cubic interpolation
In numerical analysis, a cubic Hermite spline or cubic Hermite interpolator is a spline where each piece is a third-degree polynomial specified in Hermite form, that is, by its values and first derivatives at the end points of the correspondin ...
.
History
Critical and inflection points
The critical points of a cubic function are itsstationary point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" in ...
s, that is the points where the slope of the function is zero. Thus the critical points of a cubic function defined by
:,
occur at values of such that the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
:
of the cubic function is zero.
The solutions of this equation are the -values of the critical points and are given, using the quadratic formula
In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, ...
, by
:
The sign of the expression inside the square root determines the number of critical points. If it is positive, then there are two critical points, one is a local maximum, and the other is a local minimum. If , then there is only one critical point, which is an inflection point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case ...
. If , then there are no (real) critical points. In the two latter cases, that is, if is nonpositive, the cubic function is strictly monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
. See the figure for an example of the case .
The inflection point of a function is where that function changes concavity
In calculus, the second derivative, or the second order derivative, of a function is the derivative of the derivative of . Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, ...
. An inflection point occurs when the second derivative
In calculus, the second derivative, or the second order derivative, of a function is the derivative of the derivative of . Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, ...
is zero, and the third derivative is nonzero. Thus a cubic function has always a single inflection point, which occurs at
:
Classification
translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. The English language draws a terminological distinction (which does not exist in every language) between ''transla ...
s parallel to the coordinates axes, a homothecy (uniform scaling
In affine geometry, uniform scaling (or isotropic scaling) is a linear transformation that enlarges (increases) or shrinks (diminishes) objects by a ''scale factor'' that is the same in all directions. The result of uniform scaling is similar ...
), and, possibly, a reflection (mirror image
A mirror image (in a plane mirror) is a reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical effect it results from reflection off from substance ...
) with respect to the -axis. A further non-uniform scaling can transform the graph into the graph of one among the three cubic functions
:
This means that there are only three graphs of cubic functions up to Two mathematical objects ''a'' and ''b'' are called equal up to an equivalence relation ''R''
* if ''a'' and ''b'' are related by ''R'', that is,
* if ''aRb'' holds, that is,
* if the equivalence classes of ''a'' and ''b'' with respect to ''R'' ...
an affine transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More generall ...
.
The above geometric transformation
In mathematics, a geometric transformation is any bijection of a set to itself (or to another such set) with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often b ...
s can be built in the following way, when starting from a general cubic function
Firstly, if , the change of variable
Change or Changing may refer to:
Alteration
* Impermanence, a difference in a state of affairs at different points in time
* Menopause, also referred to as "the change", the permanent cessation of the menstrual period
* Metamorphosis, or change, ...
allows supposing . After this change of variable, the new graph is the mirror image of the previous one, with respect of the -axis.
Then, the change of variable provides a function of the form
:
This corresponds to a translation parallel to the -axis.
The change of variable corresponds to a translation with respect to the -axis, and gives a function of the form
:
The change of variable corresponds to a uniform scaling, and give, after multiplication by a function of the form
:
which is the simplest form that can be obtained by a similarity.
Then, if , the non-uniform scaling gives, after division by
:
where has the value 1 or –1, depending on the sign of . If one defines the latter form of the function applies to all cases (with and ).
Symmetry
For a cubic function of the form the inflection point is thus the origin. As such a function is anodd function
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power se ...
, its graph is symmetric with respect to the inflection point, and invariant under a rotation of a half turn around the inflection point. As these properties are invariant by similarity, the following is true for all cubic functions.
''The graph of a cubic function is symmetric with respect to its inflection point, and is invariant under a rotation of a half turn around the inflection point.''
Collinearities
 The tangent lines to the graph of a cubic function at three collinear points intercept the cubic again at collinear points. This can be seen as follows.
As this property is invariant under a rigid motion, one may suppose that the function has the form
:
If is a real number, then the tangent to the graph of at the point is the line
:.
So, the intersection point between this line and the graph of can be obtained solving the equation , that is
:
which can be rewritten
:
and factorized as
:
So, the tangent intercepts the cubic at
:
So, the function that maps a point of the graph to the other point where the tangent intercepts the graph is
:
This is an
The tangent lines to the graph of a cubic function at three collinear points intercept the cubic again at collinear points. This can be seen as follows.
As this property is invariant under a rigid motion, one may suppose that the function has the form
:
If is a real number, then the tangent to the graph of at the point is the line
:.
So, the intersection point between this line and the graph of can be obtained solving the equation , that is
:
which can be rewritten
:
and factorized as
:
So, the tangent intercepts the cubic at
:
So, the function that maps a point of the graph to the other point where the tangent intercepts the graph is
:
This is an affine transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More generall ...
that transforms collinear points into collinear points. This proves the claimed result.
Cubic interpolation
Given the values of a function and its derivative at two points, there is exactly one cubic function that has the same four values, which is called a cubic Hermite spline. There are two standard ways for using this fact. Firstly, if one knows, for example by physical measurement, the values of a function and its derivative at some sampling points, one can ''interpolate'' the function with a continuously differentiable function, which is apiecewise
In mathematics, a piecewise-defined function (also called a piecewise function, a hybrid function, or definition by cases) is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. P ...
cubic function.
If the value of a function is known at several points, cubic interpolation
In numerical analysis, a cubic Hermite spline or cubic Hermite interpolator is a spline where each piece is a third-degree polynomial specified in Hermite form, that is, by its values and first derivatives at the end points of the correspondin ...
consists in approximating the function by a continuously differentiable function, which is piecewise
In mathematics, a piecewise-defined function (also called a piecewise function, a hybrid function, or definition by cases) is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. P ...
cubic. For having a uniquely defined interpolation, two more constraints must be added, such as the values of the derivatives at the endpoints, or a zero curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
at the endpoints.
Reference
External links
*History of quadratic, cubic and quartic equations
on
MacTutor archive
The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland. It contains detailed biographies on many historical and contemporary mathemati ...
.
{{DEFAULTSORT:Cubic Function
Calculus
Polynomial functions