adder (electronics) on:
[Wikipedia]
[Google]
[Amazon]
An adder, or summer, is a
File:Halfadder.gif, Half adder in action.
File:half Adder.svg, Schematic of half adder implemented with one XOR gate and one
File:Fulladder.gif, Full adder in action.
File:Full-adder logic diagram.svg, Schematic of full adder implemented with two XOR gates, two

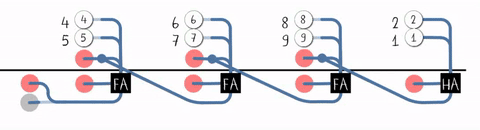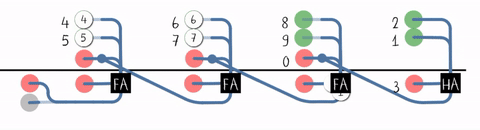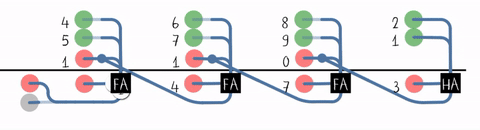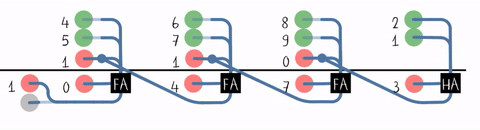 It is possible to create a logical circuit using multiple full adders to add ''N''-bit numbers. Each full adder inputs a , which is the of the previous adder. This kind of adder is called a ripple-carry adder (RCA), since each carry bit "ripples" to the next full adder. The first (and only the first) full adder may be replaced by a half adder (under the assumption that ).
The layout of a ripple-carry adder is simple, which allows fast design time; however, the ripple-carry adder is relatively slow, since each full adder must wait for the carry bit to be calculated from the previous full adder. The gate delay can easily be calculated by inspection of the full adder circuit. Each full adder requires three levels of logic. In a 32-bit ripple-carry adder, there are 32 full adders, so the critical path (worst case) delay is 3 (from input to of first adder) + 31 × 2 (for carry propagation in latter adders) = 65 gate delays.
The general equation for the worst-case delay for a ''n''-bit carry-ripple adder, accounting for both the sum and carry bits, is:
:
A design with alternating carry polarities and optimized AND-OR-Invert gates can be about twice as fast.
It is possible to create a logical circuit using multiple full adders to add ''N''-bit numbers. Each full adder inputs a , which is the of the previous adder. This kind of adder is called a ripple-carry adder (RCA), since each carry bit "ripples" to the next full adder. The first (and only the first) full adder may be replaced by a half adder (under the assumption that ).
The layout of a ripple-carry adder is simple, which allows fast design time; however, the ripple-carry adder is relatively slow, since each full adder must wait for the carry bit to be calculated from the previous full adder. The gate delay can easily be calculated by inspection of the full adder circuit. Each full adder requires three levels of logic. In a 32-bit ripple-carry adder, there are 32 full adders, so the critical path (worst case) delay is 3 (from input to of first adder) + 31 × 2 (for carry propagation in latter adders) = 65 gate delays.
The general equation for the worst-case delay for a ''n''-bit carry-ripple adder, accounting for both the sum and carry bits, is:
:
A design with alternating carry polarities and optimized AND-OR-Invert gates can be about twice as fast.

 To reduce the computation time, Weinberger and Smith invented a faster way to add two binary numbers by using carry-lookahead adders (CLA). They introduced two signals ( and ) for each bit position, based on whether a carry is propagated through from a less significant bit position (at least one input is a 1), generated in that bit position (both inputs are 1), or killed in that bit position (both inputs are 0). In most cases, is simply the sum output of a half adder and is the carry output of the same adder. After and are generated, the carries for every bit position are created.
Mere derivation of Weinberger-Smith CLA recurrence, are: Brent–Kung adder (BKA), and the Kogge–Stone adder (KSA).
This was shown in Oklobdzija and Zeydel paper in IEEE Journal of Solid-State Circuits.
Some other multi-bit adder architectures break the adder into blocks. It is possible to vary the length of these blocks based on the
To reduce the computation time, Weinberger and Smith invented a faster way to add two binary numbers by using carry-lookahead adders (CLA). They introduced two signals ( and ) for each bit position, based on whether a carry is propagated through from a less significant bit position (at least one input is a 1), generated in that bit position (both inputs are 1), or killed in that bit position (both inputs are 0). In most cases, is simply the sum output of a half adder and is the carry output of the same adder. After and are generated, the carries for every bit position are created.
Mere derivation of Weinberger-Smith CLA recurrence, are: Brent–Kung adder (BKA), and the Kogge–Stone adder (KSA).
This was shown in Oklobdzija and Zeydel paper in IEEE Journal of Solid-State Circuits.
Some other multi-bit adder architectures break the adder into blocks. It is possible to vary the length of these blocks based on the
 Using only the Toffoli and CNOT quantum logic gates, it is possible to produce quantum full- and half-adders. The same circuits can also be implemented in classical reversible computation, as both CNOT and Toffoli are also classical
Using only the Toffoli and CNOT quantum logic gates, it is possible to produce quantum full- and half-adders. The same circuits can also be implemented in classical reversible computation, as both CNOT and Toffoli are also classical
8-bit Full Adder and Subtractor
a demonstration of an interactive Full Adder built in JavaScript solely for learning purposes. * * {{DEFAULTSORT:Adder (Electronics) Binary arithmetic Adders (electronics)
digital circuit
In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematica ...
that performs addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
of numbers. In many computer
A computer is a machine that can be Computer programming, programmed to automatically Execution (computing), carry out sequences of arithmetic or logical operations (''computation''). Modern digital electronic computers can perform generic set ...
s and other kinds of processors, adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate address
An address is a collection of information, presented in a mostly fixed format, used to give the location of a building, apartment, or other structure or a plot of land, generally using border, political boundaries and street names as references, ...
es, table indices, increment and decrement operators and similar operations.
Although adders can be constructed for many number representations, such as binary-coded decimal or excess-3, the most common adders operate on binary number
A binary number is a number expressed in the Radix, base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may ...
s.
In cases where two's complement
Two's complement is the most common method of representing signed (positive, negative, and zero) integers on computers, and more generally, fixed point binary values. Two's complement uses the binary digit with the ''greatest'' value as the ''s ...
or ones' complement
The ones' complement of a binary number is the value obtained by inverting (flipping) all the bits in the Binary number, binary representation of the number. The name "ones' complement" refers to the fact that such an inverted value, if added t ...
is being used to represent negative number
In mathematics, a negative number is the opposite (mathematics), opposite of a positive real number. Equivalently, a negative number is a real number that is inequality (mathematics), less than 0, zero. Negative numbers are often used to represe ...
s, it is trivial to modify an adder into an adder–subtractor.
Other signed number representations
In computing, signed number representations are required to encode negative numbers in binary number systems.
In mathematics, negative numbers in any base are represented by prefixing them with a minus sign ("−"). However, in RAM or CPU reg ...
require more logic around the basic adder.
History
George Stibitz
George Robert Stibitz (April 30, 1904 – January 31, 1995) was an American researcher at Bell Labs who is internationally recognized as one of the fathers of the modern digital computer. He was known for his work in the 1930s and 1940s on the r ...
invented the 2-bit binary adder (the Model K) in 1937.
Binary adders
Half adder
The half adder adds two single binary digits and . It has two outputs, sum () and carry (). The carry signal represents an overflow into the next digit of a multi-digit addition. The value of the sum is . The simplest half-adder design, pictured on the right, incorporates an XOR gate for and anAND gate
The AND gate is a basic digital logic gate that implements the logical conjunction (∧) from mathematical logic AND gates behave according to their truth table. A HIGH output (1) results only if all the inputs to the AND gate are HIGH (1). If a ...
for . The Boolean logic for the sum (in this case ) will be whereas for the carry () will be . With the addition of an OR gate to combine their carry outputs, two half adders can be combined to make a full adder.
The truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arg ...
for the half adder is:
:
Various half adder digital logic circuits:
AND gate
The AND gate is a basic digital logic gate that implements the logical conjunction (∧) from mathematical logic AND gates behave according to their truth table. A HIGH output (1) results only if all the inputs to the AND gate are HIGH (1). If a ...
.
File:Half adder using NAND gates only.jpg, Schematic of half adder implemented with five NAND gates.
File:1-bit half-adder.svg, Schematic symbol for a 1-bit half adder.
Full adder
A full adder adds binary numbers and accounts for values carried in as well as out. A one-bit full-adder adds three one-bit numbers, often written as , , and ; and are the operands, and is a bit carried in from the previous less-significant stage. The circuit produces a two-bit output. Output carry and sum are typically represented by the signals and , where the sum equals . The full adder is usually a component in a cascade of adders, which add 8, 16, 32, etc. bit binary numbers. A full adder can be implemented in many different ways such as with a customtransistor
A transistor is a semiconductor device used to Electronic amplifier, amplify or electronic switch, switch electrical signals and electric power, power. It is one of the basic building blocks of modern electronics. It is composed of semicondu ...
-level circuit or composed of other gates. The most common implementation is with:
:
:
The above expressions for and can be derived from using a Karnaugh map
A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of ...
to simplify the truth table.
In this implementation, the final OR gate before the carry-out output may be replaced by an XOR gate without altering the resulting logic. This is because when A and B are both 1, the term is always 0, and hence can only be 0. Thus, the inputs to the final OR gate can never be both 1 (this is the only combination for which the OR and XOR outputs differ).
Due to the functional completeness
In Mathematical logic, logic, a functionally complete set of logical connectives or Boolean function, Boolean operators is one that can be used to express all possible truth tables by combining members of the Set (mathematics), set into a Boolean ...
property of the NAND and NOR gates, a full adder can also be implemented using nine NAND gates, or nine NOR gates.
Using only two types of gates is convenient if the circuit is being implemented using simple integrated circuit
An integrated circuit (IC), also known as a microchip or simply chip, is a set of electronic circuits, consisting of various electronic components (such as transistors, resistors, and capacitors) and their interconnections. These components a ...
chips which contain only one gate type per chip.
A full adder can also be constructed from two half adders by connecting and to the input of one half adder, then taking its sum-output as one of the inputs to the second half adder and as its other input, and finally the carry outputs from the two half-adders are connected to an OR gate. The sum-output from the second half adder is the final sum output () of the full adder and the output from the OR gate is the final carry output (). The critical path of a full adder runs through both XOR gates and ends at the sum bit . Assumed that an XOR gate takes 1 delays to complete, the delay imposed by the critical path of a full adder is equal to:
:
The critical path of a carry runs through one XOR gate in adder and through 2 gates (AND and OR) in carry-block and therefore, if AND or OR gates take 1 delay to complete, has a delay of:
:
The truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arg ...
for the full adder is:
:
Inverting all inputs of a full adder also inverts all of its outputs, which can be used in the design of fast ripple-carry adders, because there is no need to invert the carry.
Various full adder digital logic circuits:
AND gate
The AND gate is a basic digital logic gate that implements the logical conjunction (∧) from mathematical logic AND gates behave according to their truth table. A HIGH output (1) results only if all the inputs to the AND gate are HIGH (1). If a ...
s, one OR gate.
File:Full Adder using NAND gates.svg, Schematic of full adder implemented with nine NAND gates.
File:Full Adder using NOR gates.svg, Schematic of full adder implemented with nine NOR gates.
File:Inverting full adder CMOS 24T.svg, Full adder with inverted outputs with single-transistor carry propagation delay in CMOS
File:1-bit full-adder.svg, Schematic symbol for a 1-bit full adder with ''C''in and ''C''out drawn on sides of block to emphasize their use in a multi-bit adder
Adders supporting multiple bits
Ripple-carry adder
 It is possible to create a logical circuit using multiple full adders to add ''N''-bit numbers. Each full adder inputs a , which is the of the previous adder. This kind of adder is called a ripple-carry adder (RCA), since each carry bit "ripples" to the next full adder. The first (and only the first) full adder may be replaced by a half adder (under the assumption that ).
The layout of a ripple-carry adder is simple, which allows fast design time; however, the ripple-carry adder is relatively slow, since each full adder must wait for the carry bit to be calculated from the previous full adder. The gate delay can easily be calculated by inspection of the full adder circuit. Each full adder requires three levels of logic. In a 32-bit ripple-carry adder, there are 32 full adders, so the critical path (worst case) delay is 3 (from input to of first adder) + 31 × 2 (for carry propagation in latter adders) = 65 gate delays.
The general equation for the worst-case delay for a ''n''-bit carry-ripple adder, accounting for both the sum and carry bits, is:
:
A design with alternating carry polarities and optimized AND-OR-Invert gates can be about twice as fast.
It is possible to create a logical circuit using multiple full adders to add ''N''-bit numbers. Each full adder inputs a , which is the of the previous adder. This kind of adder is called a ripple-carry adder (RCA), since each carry bit "ripples" to the next full adder. The first (and only the first) full adder may be replaced by a half adder (under the assumption that ).
The layout of a ripple-carry adder is simple, which allows fast design time; however, the ripple-carry adder is relatively slow, since each full adder must wait for the carry bit to be calculated from the previous full adder. The gate delay can easily be calculated by inspection of the full adder circuit. Each full adder requires three levels of logic. In a 32-bit ripple-carry adder, there are 32 full adders, so the critical path (worst case) delay is 3 (from input to of first adder) + 31 × 2 (for carry propagation in latter adders) = 65 gate delays.
The general equation for the worst-case delay for a ''n''-bit carry-ripple adder, accounting for both the sum and carry bits, is:
:
A design with alternating carry polarities and optimized AND-OR-Invert gates can be about twice as fast.
Carry-lookahead adder (Weinberger and Smith, 1958)
propagation delay
Propagation delay is the time duration taken for a signal to reach its destination, for example in the electromagnetic field, a wire, speed of sound, gas, fluid or seismic wave, solid body.
Physics
* An electromagnetic wave travelling through ...
of the circuits to optimize computation time. These block based adders include the carry-skip (or carry-bypass) adder which will determine and values for each block rather than each bit, and the carry-select adder which pre-generates the sum and carry values for either possible carry input (0 or 1) to the block, using multiplexers to select the appropriate result ''when'' the carry bit is known.
By combining multiple carry-lookahead adders, even larger adders can be created. This can be used at multiple levels to make even larger adders. For example, the following adder is a 64-bit adder that uses four 16-bit CLAs with two levels of lookahead carry units.
Other adder designs include the carry-select adder, conditional sum adder, carry-skip adder, and carry-complete adder.
Carry-save adders
If an adding circuit is to compute the sum of three or more numbers, it can be advantageous to not propagate the carry result. Instead, three-input adders are used, generating two results: a sum and a carry. The sum and the carry may be fed into two inputs of the subsequent 3-number adder without having to wait for propagation of a carry signal. After all stages of addition, however, a conventional adder (such as the ripple-carry or the lookahead) must be used to combine the final sum and carry results.3:2 compressors
A full adder can be viewed as a ''3:2 lossy compressor'': it sums three one-bit inputs and returns the result as a single two-bit number; that is, it maps 8 input values to 4 output values. (the term "compressor" instead of "counter" was introduced in)Thus, for example, a binary input of 101 results in an output of (decimal number 2). The carry-out represents bit one of the result, while the sum represents bit zero. Likewise, a half adder can be used as a ''2:2 lossy compressor'', compressing four possible inputs into three possible outputs. Such compressors can be used to speed up the summation of three or more addends. If the number of addends is exactly three, the layout is known as the carry-save adder. If the number of addends is four or more, more than one layer of compressors is necessary, and there are various possible designs for the circuit: the most common are Dadda and Wallace trees. This kind of circuit is most notably used in multiplier circuits, which is why these circuits are also known as Dadda and Wallace multipliers.Quantum adders
 Using only the Toffoli and CNOT quantum logic gates, it is possible to produce quantum full- and half-adders. The same circuits can also be implemented in classical reversible computation, as both CNOT and Toffoli are also classical
Using only the Toffoli and CNOT quantum logic gates, it is possible to produce quantum full- and half-adders. The same circuits can also be implemented in classical reversible computation, as both CNOT and Toffoli are also classical logic gate
A logic gate is a device that performs a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one that has, for ...
s.
Since the quantum Fourier transform has a low circuit complexity, it can efficiently be used for adding numbers as well.
Analog adders
Just as in Binary adders, combining two input currents effectively adds those currents together. Within the constraints of the hardware, non-binary signals (i.e. with a base higher than 2) can be added together to calculate a sum. Also known as a "summing amplifier", this technique can be used to reduce the number of transistors in an addition circuit.See also
* Binary multiplier * Subtractor * Electronic mixer — for adding analog signalsReferences
Further reading
* * * * *External links
*8-bit Full Adder and Subtractor
a demonstration of an interactive Full Adder built in JavaScript solely for learning purposes. * * {{DEFAULTSORT:Adder (Electronics) Binary arithmetic Adders (electronics)