Zone Axis on:
[Wikipedia]
[Google]
[Amazon]
 Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the
Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the
pdf
/ref> Direct lattice vectors have components measured in distance units, like meters (m) or
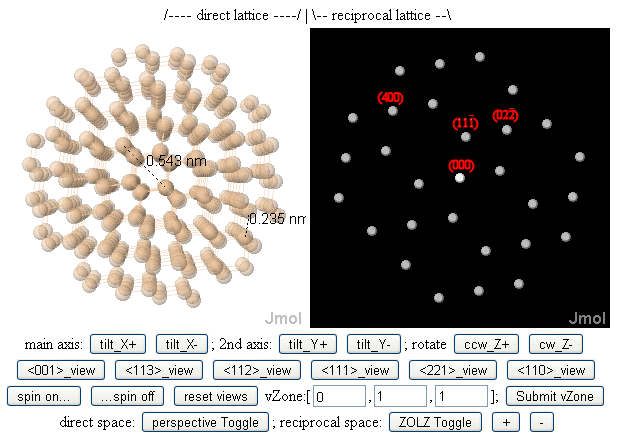 One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low- Miller index" lattice planes, which in turn have small spatial frequencies (g-values) and hence large lattice periodicities (d-spacings). A possible intuition behind this is that in electron microscopy, for electron beams to be directed down wide (i.e. easily visible) tunnels between columns of atoms in a crystal, directing the beam down a low-index (and by association high-symmetry) zone axis may help.J. W. Edington (1976) ''Practical electron microscopy in materials science'' (N. V. Philips' Gloeilampenfabrieken, Eindhoven) Ludwig Reimer (1997 4th ed) ''Transmission electron microscopy: Physics of image formation and microanalysis'' (Springer, Berlin
One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low- Miller index" lattice planes, which in turn have small spatial frequencies (g-values) and hence large lattice periodicities (d-spacings). A possible intuition behind this is that in electron microscopy, for electron beams to be directed down wide (i.e. easily visible) tunnels between columns of atoms in a crystal, directing the beam down a low-index (and by association high-symmetry) zone axis may help.J. W. Edington (1976) ''Practical electron microscopy in materials science'' (N. V. Philips' Gloeilampenfabrieken, Eindhoven) Ludwig Reimer (1997 4th ed) ''Transmission electron microscopy: Physics of image formation and microanalysis'' (Springer, Berlin
preview
David B. Williams and C. Barry Carter (1996) ''Transmission electron microscopy: A textbook for materials science'' (Plenum Press, NY) P. Hirsch, A. Howie, R. Nicholson, D. W. Pashley and M. J. Whelan (1965/1977) ''Electron microscopy of thin crystals'' (Butterworths/Krieger, London/Malabar FL)
International Tables for Crystallography
Materials science Crystals Electron microscopy Crystallography Diffraction
 Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the
Zone axis, a term sometimes used to refer to "high-symmetry" orientations in a crystal, most generally refers to ''any'' direction referenced to the direct lattice (as distinct from the reciprocal lattice
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier tran ...
) of a crystal in three dimensions. It is therefore indexed with direct lattice indices, instead of with Miller indices.
High-symmetry zone axes through a crystal lattice, in particular, often lie in the direction of tunnels through the crystal between planes of atoms. This is because, as we see below, such zone axis directions generally lie within more than one plane of atoms in the crystal.
Zone-axis indexing
Thetranslational invariance
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation.
Analogously, an oper ...
of a crystal lattice
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystal, crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that ...
is described by a set of unit cell, direct lattice basis vectors ( contravariantGeorge Arfken (1970) ''Mathematical methods for physicists'' (Academic Press, New York). or polar) called a, b, and c, or equivalently by the lattice parameters, i.e. the magnitudes of the vectors, called ''a'', ''b'' and ''c'', and the angles between them, called ''α'' (between b and c), ''β'' (between c and a), and ''γ'' (between a and b).J. M. Ziman (1972 2nd ed) ''Principles of the theory of solids'' (Cambridge U. Press, Cambridge UK).Zbigniew Dauter and Mariusz Jaskolski (2010) "How to read (and understand) Volume A of International Tables for Crystallography: an introduction for nonspecialists", ''J. Appl. Crystallogr.'' 43, 1150–117/ref> Direct lattice vectors have components measured in distance units, like meters (m) or
angstrom
The angstrom (; ) is a unit of length equal to m; that is, one ten-billionth of a metre, a hundred-millionth of a centimetre, 0.1 nanometre, or 100 picometres. The unit is named after the Swedish physicist Anders Jonas Ångström (1814–18 ...
s (Å).
A lattice vector is indexed by its coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the Position (geometry), position of the Point (geometry), points or other geometric elements on a manifold such as ...
in the direct lattice basis system and is generally placed between square brackets []. Thus a direct lattice vector , or , is defined as . Angle brackets ⟨⟩ are used to refer to a symmetrically equivalent class of lattice vectors (i.e. the set of vectors generated by an action of the lattice's symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
). In the case of a cubic lattice, for instance, ⟨100⟩ represents 00 10 01 0 0and 0because each of these vectors is symmetrically equivalent under a 90 degree rotation along an axis. A bar over a coordinate is equivalent to a negative sign (e.g., ).
The term "zone axis" more specifically refers to the direction of a direct-space lattice vector. For example, since the 20and 40lattice vectors are parallel, their orientations both correspond the ⟨120⟩ zone of the crystal. Just as a set of lattice planes in direct space corresponds to a reciprocal lattice
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier tran ...
vector in the complementary space of spatial frequencies and momenta, a "zone" is definedE. W. Nuffield (1966) ''X-ray diffraction methods'' (John Wiley, NY).B. E. Warren (1969) ''X-ray diffraction'' (Addison-Wesley, paperback edition by Dover Books 1990) . as a set of reciprocal lattice planes in frequency space that corresponds to a lattice vector in direct space.
The reciprocal space analog to a zone axis is a "lattice plane normal" or "g-vector direction". Reciprocal lattice vectors ( one-formcf. Charles W. Misner, Kip S. Thorne and John Archibald Wheeler (1973) ''Gravitation'' (W. H. Freeman, San Francisco CA). or axial) are Miller-indexed using coordinates in the reciprocal lattice basis instead, generally between round brackets () (similar to square brackets [] for direct lattice vectors). Curly brackets (not to be confused with a mathematical Set (mathematics)#How sets are defined and set notation, set) are used to refer to a symmetrically equivalent class of reciprocal lattice vectors, similar to angle brackets ⟨⟩ for classes of direct lattice vectors.
Here, , , and , where the unit cell volume is ( denotes a dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
and a cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
). Thus a reciprocal lattice vector or has a direction perpendicular to a crystallographic plane and a magnitude equal to the reciprocal of the spacing between those planes, measured in spatial frequency units, e.g. of cycles per angstrom (cycles/Å).
A useful and quite general rule of crystallographic " dual vector spaces in 3D", e.g. reciprocal lattices, is that the condition for a direct lattice vector 'uvw''(or zone axis) to be perpendicular to a reciprocal lattice vector (''hkl'') can be written with a dot product as . This is true even if, as is often the case, the basis vector set used to describe the lattice is not Cartesian.
Zone-axis patterns
By extension, a 'uvw''zone-axis pattern (ZAP) is adiffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
pattern taken with an incident beam, e.g. of electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
s, X-ray
An X-ray (also known in many languages as Röntgen radiation) is a form of high-energy electromagnetic radiation with a wavelength shorter than those of ultraviolet rays and longer than those of gamma rays. Roughly, X-rays have a wavelength ran ...
s or neutron
The neutron is a subatomic particle, symbol or , that has no electric charge, and a mass slightly greater than that of a proton. The Discovery of the neutron, neutron was discovered by James Chadwick in 1932, leading to the discovery of nucle ...
s traveling along a lattice direction specified by the zone-axis indices 'uvw'' Because of their small wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
''λ'', high energy electrons used in electron microscope
An electron microscope is a microscope that uses a beam of electrons as a source of illumination. It uses electron optics that are analogous to the glass lenses of an optical light microscope to control the electron beam, for instance focusing it ...
s have a very large Ewald sphere radius (1/λ), so that electron diffraction generally "lights up" diffraction spots with g-vectors (''hkl'') that are perpendicular to 'uvw''John M. Cowley (1975) ''Diffraction Physics'' (North-Holland, Amsterdam).
 One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low- Miller index" lattice planes, which in turn have small spatial frequencies (g-values) and hence large lattice periodicities (d-spacings). A possible intuition behind this is that in electron microscopy, for electron beams to be directed down wide (i.e. easily visible) tunnels between columns of atoms in a crystal, directing the beam down a low-index (and by association high-symmetry) zone axis may help.J. W. Edington (1976) ''Practical electron microscopy in materials science'' (N. V. Philips' Gloeilampenfabrieken, Eindhoven) Ludwig Reimer (1997 4th ed) ''Transmission electron microscopy: Physics of image formation and microanalysis'' (Springer, Berlin
One result of this, as illustrated in the figure above, is that "low-index" zones are generally perpendicular to "low- Miller index" lattice planes, which in turn have small spatial frequencies (g-values) and hence large lattice periodicities (d-spacings). A possible intuition behind this is that in electron microscopy, for electron beams to be directed down wide (i.e. easily visible) tunnels between columns of atoms in a crystal, directing the beam down a low-index (and by association high-symmetry) zone axis may help.J. W. Edington (1976) ''Practical electron microscopy in materials science'' (N. V. Philips' Gloeilampenfabrieken, Eindhoven) Ludwig Reimer (1997 4th ed) ''Transmission electron microscopy: Physics of image formation and microanalysis'' (Springer, Berlinpreview
David B. Williams and C. Barry Carter (1996) ''Transmission electron microscopy: A textbook for materials science'' (Plenum Press, NY) P. Hirsch, A. Howie, R. Nicholson, D. W. Pashley and M. J. Whelan (1965/1977) ''Electron microscopy of thin crystals'' (Butterworths/Krieger, London/Malabar FL)
See also
*Crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
* Dual basis
In linear algebra, given a vector space V with a basis B of vectors indexed by an index set I (the cardinality of I is the dimension of V), the dual set of B is a set B^* of vectors in the dual space V^* with the same index set I such that B and ...
* Reciprocal lattice
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier tran ...
* Miller index
* Diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
* Electron diffraction
* Transmission electron microscopy
Transmission electron microscopy (TEM) is a microscopy technique in which a beam of electrons is transmitted through a specimen to form an image. The specimen is most often an ultrathin section less than 100 nm thick or a suspension on a g ...
Footnotes
{{ReflistExternal links
International Tables for Crystallography
Materials science Crystals Electron microscopy Crystallography Diffraction