Zero-inflated Model on:
[Wikipedia]
[Google]
[Amazon]
In statistics, a zero-inflated model is a
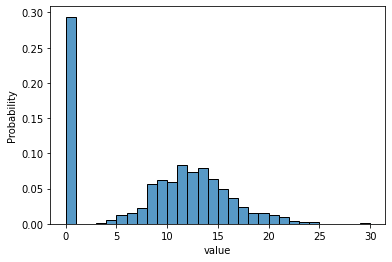 One well-known zero-inflated model is Diane Lambert's zero-inflated Poisson model, which concerns a random event containing excess zero-count data in unit time. For example, the number of insurance claims within a population for a certain type of risk would be zero-inflated by those people who have not taken out insurance against the risk and thus are unable to claim. The zero-inflated Poisson (ZIP) model mixes two zero generating processes. The first process generates zeros. The second process is governed by a
One well-known zero-inflated model is Diane Lambert's zero-inflated Poisson model, which concerns a random event containing excess zero-count data in unit time. For example, the number of insurance claims within a population for a certain type of risk would be zero-inflated by those people who have not taken out insurance against the risk and thus are unable to claim. The zero-inflated Poisson (ZIP) model mixes two zero generating processes. The first process generates zeros. The second process is governed by a
pscl
an
brms
R packages
statistical model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of sample data (and similar data from a larger population). A statistical model represents, often in considerably idealized form, ...
based on a zero-inflated probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
, i.e. a distribution that allows for frequent zero-valued observations.
Zero-inflated Poisson
 One well-known zero-inflated model is Diane Lambert's zero-inflated Poisson model, which concerns a random event containing excess zero-count data in unit time. For example, the number of insurance claims within a population for a certain type of risk would be zero-inflated by those people who have not taken out insurance against the risk and thus are unable to claim. The zero-inflated Poisson (ZIP) model mixes two zero generating processes. The first process generates zeros. The second process is governed by a
One well-known zero-inflated model is Diane Lambert's zero-inflated Poisson model, which concerns a random event containing excess zero-count data in unit time. For example, the number of insurance claims within a population for a certain type of risk would be zero-inflated by those people who have not taken out insurance against the risk and thus are unable to claim. The zero-inflated Poisson (ZIP) model mixes two zero generating processes. The first process generates zeros. The second process is governed by a Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known ...
that generates counts, some of which may be zero. The mixture distribution
In probability and statistics, a mixture distribution is the probability distribution of a random variable that is derived from a collection of other random variables as follows: first, a random variable is selected by chance from the collection ...
is described as follows:
:
:
where the outcome variable has any non-negative integer value, is the expected Poisson count for the th individual; is the probability of extra zeros.
The mean is and the variance is .
Estimators of ZIP parameters
The method of moments estimators are given by : : where is the sample mean and is the sample variance. The maximum likelihood estimator can be found by solving the following equation : where is the observed proportion of zeros. A closed form solution of this equation is given by : with being the main branch of Lambert's W-function and :. Alternatively, the equation can be solved by iteration. The maximum likelihood estimator for is given by :Related models
In 1994, Greene considered the zero-inflated negative binomial (ZINB) model. Daniel B. Hall adapted Lambert's methodology to an upper-bounded count situation, thereby obtaining a zero-inflated binomial (ZIB) model.Discrete pseudo compound Poisson model
If the count data is such that the probability of zero is larger than the probability of nonzero, namely : then the discrete data obey discrete pseudocompound Poisson distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. T ...
.
In fact, let be the probability generating function of . If , then . Then from the Wiener–Lévy theorem, has the probability generating function of the discrete pseudo compound Poisson distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. T ...
.
We say that the discrete random variable satisfying probability generating function characterization
:
has a discrete pseudo compound Poisson distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. T ...
with parameters
:
When all the are non-negative, it is the discrete compound Poisson distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. T ...
(non-Poisson case) with overdispersion
In statistics, overdispersion is the presence of greater variability (statistical dispersion) in a data set than would be expected based on a given statistical model.
A common task in applied statistics is choosing a parametric model to fit a g ...
property.
See also
*Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known ...
* Zero-truncated Poisson distribution
In probability theory, the zero-truncated Poisson (ZTP) distribution is a certain discrete probability distribution whose support is the set of positive integers. This distribution is also known as the conditional Poisson distribution or the pos ...
* Compound Poisson distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. T ...
* Sparse approximation
* Hurdle model
Software
pscl
an
brms
R packages
References
{{least squares and regression analysis Generalized linear models Categorical data Poisson point processes