Wave Action (continuum Mechanics)

In continuum mechanics, wave action refers to a conservable measure of the wave part of a motion. For small- amplitude and slowly varying waves, the wave action density is:

:$\mathcal = \frac,$

where $E$ is the intrinsic wave energy and $\omega_i$ is the intrinsic frequency of the slowly modulated waves – intrinsic here implying: as observed in a frame of reference moving with the mean velocity of the motion.

The action of a wave was introduced by in the study of the (pseudo) energy and momentum of waves in plasmas. derived the conservation of wave action – identified as an adiabatic invariant – from an averaged Lagrangian description of slowly varying nonlinear wave trains in inhomogeneous media:

:$\frac\mathcal + \boldsymbol \cdot \boldsymbol = 0,$

where $\boldsymbol$ is the wave-action density flux and $\boldsymbol\cdot\boldsymbol$ is the divergence of $\boldsymbol$. The description of waves in inhomogeneous and moving media was further elaborated by for the case of small-amplitude waves; they also called the quantity ''wave action'' (by which name it has been referred to subsequently). For small-amplitude waves the conservation of wave action becomes:

:\frac\left( \frac \right) + \boldsymbol \cdot \left \left( \boldsymbol + \boldsymbol_g \right)\, \frac \right= 0, using $\mathcal = \frac$ and $\boldsymbol = \left( \boldsymbol + \boldsymbol_g \right) \mathcal,$

where $\boldsymbol_g$ is the group velocity and $\boldsymbol$ the mean velocity of the inhomogeneous moving medium. While the ''total energy'' (the sum of the energies of the mean motion and of the wave motion) is conserved for a non-dissipative system, the energy of the wave motion is not conserved, since in general there can be an exchange of energy with the mean motion. However, wave action is a quantity which is conserved for the wave-part of the motion.

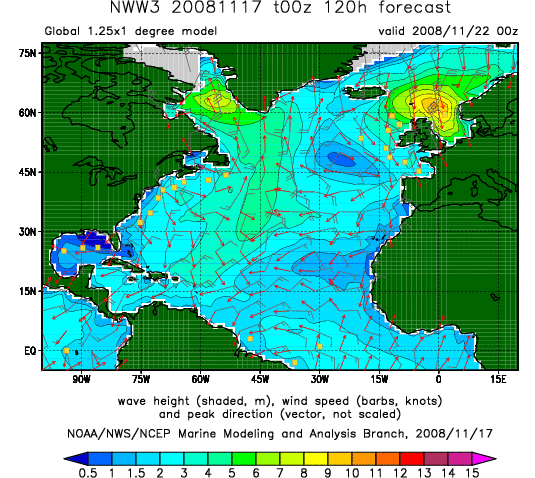
The equation for the conservation of wave action is for instance used extensively in wind wave models to forecast sea states as needed by mariners, the offshore industry and for coastal defense. Also in plasma physics and acoustics the concept of wave action is used.

The derivation of an exact wave-action equation for more general wave motion – not limited to slowly modulated waves, small-amplitude waves or (non-dissipative) conservative systems – was provided and analysed by using the framework of the generalised Lagrangian mean for the separation of wave and mean motion.

Notes

References

*
*
*
*
*
*
*
*
*
*

{{physical oceanography

Continuum mechanics
Waves