Watt's curve on:
[Wikipedia]
[Google]
[Amazon]


 In mathematics, Watt's curve is a tricircular
In mathematics, Watt's curve is a tricircular
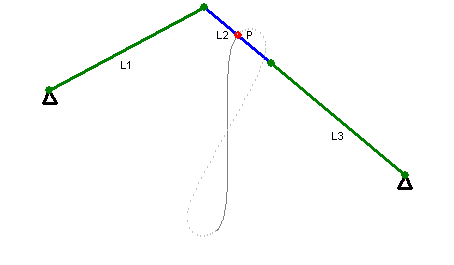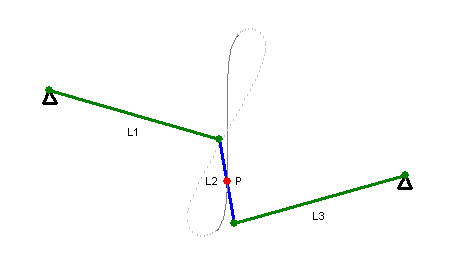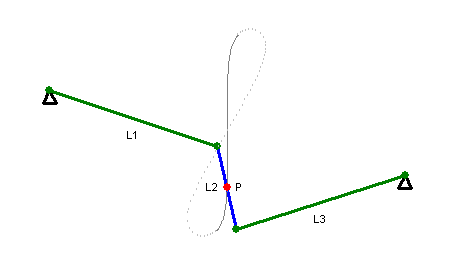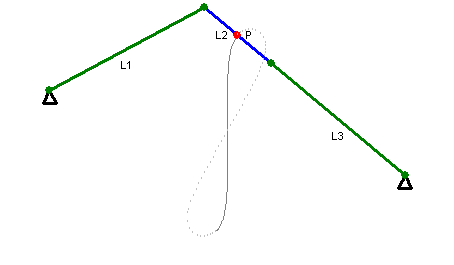 When the curve crosses the origin, the origin is a point of inflection and therefore has contact of order 3 with a tangent. However, if ( which is the case if the triangle with sides , and is a right triangle) then tangent has contact of order 5 with the tangent, in other words the curve is a close approximation of a straight line. This is the basis for Watt's linkage.
When the curve crosses the origin, the origin is a point of inflection and therefore has contact of order 3 with a tangent. However, if ( which is the case if the triangle with sides , and is a right triangle) then tangent has contact of order 5 with the tangent, in other words the curve is a close approximation of a straight line. This is the basis for Watt's linkage.


 In mathematics, Watt's curve is a tricircular
In mathematics, Watt's curve is a tricircular plane algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane ...
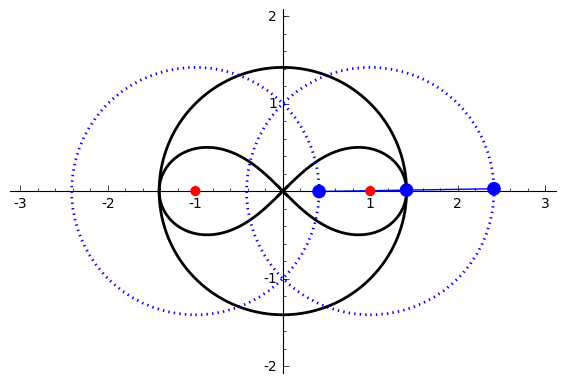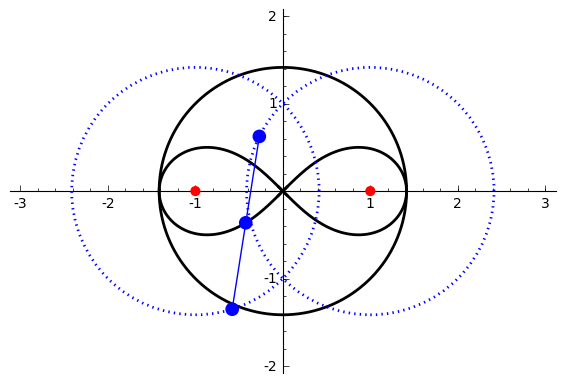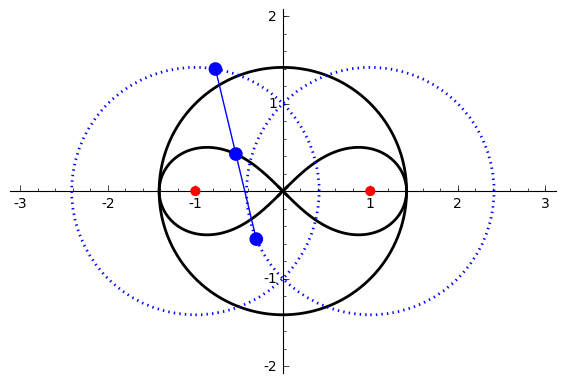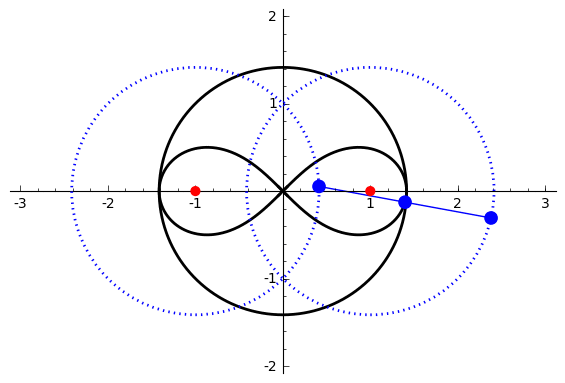
of degree six. It is generated by two circles of radius ''b'' with centers distance 2''a'' apart (taken to be at (±''a'', 0)). A line segment of length 2''c'' attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine.
The equation of the curve can be given in polar coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to t ...
as
:
Derivation
Polar coordinates
The polar equation for the curve can be derived as follows: Working in thecomplex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
, let the centers of the circles be at ''a'' and ''−a'', and the connecting segment have endpoints at ''−a''+''be''''i'' λ and ''a''+''be''''i'' ρ. Let the angle of inclination of the segment be ψ with its midpoint at ''re''''i'' θ. Then the endpoints are also given by ''re''''i'' θ ± ''ce''''i'' ψ. Setting expressions for the same points equal to each other gives
:
:
Add these and divide by two to get
:
Comparing radii and arguments gives
:
Similarly, subtracting the first two equations and dividing by 2 gives
:
Write
:
Then
:
:
:
:
Cartesian coordinates
Expanding the polar equation gives : : : : : Letting ''d'' 2=''a''2+''b''2–''c''2 simplifies this to :Form of the curve
The construction requires a quadrilateral with sides 2''a'', ''b'', 2''c'', ''b''. Any side must be less than the sum of the remaining sides, so the curve is empty (at least in the real plane) unless ''a''<''b''+''c'' and ''c''<''b''+''a''. The curve has a crossing point at the origin if there is a triangle with sides ''a'', ''b'' and ''c''. Given the previous conditions, this means that the curve crosses the origin if and only if ''b''<''a''+''c''. If ''b''=''a''+''c'' then two branches of the curve meet at the origin with a common vertical tangent, making it a quadruple point. Given ''b''<''a''+''c'', the shape of the curve is determined by the relative magnitude of ''b'' and ''d''. If ''d'' is imaginary, that is if ''a''2+''b''2 <''c''2 then the curve has the form of a figure eight. If ''d'' is 0 then the curve is a figure eight with two branches of the curve having a common horizontal tangent at the origin. If 0<''d''<''b'' then the curve has two additional double points at ±''d'' and the curve crosses itself at these points. The overall shape of the curve is pretzel-like in this case. If ''d''=''b'' then ''a''=''c'' and the curve decomposes into a circle of radius ''b'' and a lemniscate of Booth, a figure eight shaped curve. A special case of this is ''a''=''c'', ''b''=√2''c'' which produces thelemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points and , known as foci, at distance from each other as the locus of points so that . The curve has a shape similar to the numeral 8 and to the ∞ symbol. ...
. Finally, if ''d''>''b'' then the points ±''d'' are still solutions to the Cartesian equation of the curve, but the curve does not cross these points and they are acnode
An acnode is an isolated point in the solution set of a polynomial equation in two real variables. Equivalent terms are " isolated point or hermit point".
For example the equation
:f(x,y)=y^2+x^2-x^3=0
has an acnode at the origin, because it is ...
s. The curve again has a figure eight shape though the shape is distorted if ''d'' is close to ''b''.
Given ''b''>''a''+''c'', the shape of the curve is determined by the relative sizes of ''a'' and ''c''. If ''a''<''c'' then the curve has the form of two loops that cross each other at ±''d''. If ''a''=''c'' then the curve decomposes into a circle of radius ''b'' and an oval of Booth. If ''a''>''c'' then the curve does not cross the ''x''-axis at all and consists of two flattened ovals.Encyclopédie des Formes Mathématiques Remarquables page for section.
Watt's linkage
 When the curve crosses the origin, the origin is a point of inflection and therefore has contact of order 3 with a tangent. However, if ( which is the case if the triangle with sides , and is a right triangle) then tangent has contact of order 5 with the tangent, in other words the curve is a close approximation of a straight line. This is the basis for Watt's linkage.
When the curve crosses the origin, the origin is a point of inflection and therefore has contact of order 3 with a tangent. However, if ( which is the case if the triangle with sides , and is a right triangle) then tangent has contact of order 5 with the tangent, in other words the curve is a close approximation of a straight line. This is the basis for Watt's linkage.
See also
*Four-bar linkage
In the study of mechanisms, a four-bar linkage, also called a four-bar, is the simplest closed-chain movable linkage. It consists of four bodies, called ''bars'' or ''links'', connected in a loop by four joints. Generally, the joints are configu ...
* Watt's linkage
In kinematics, Watt's linkage (also known as the parallel linkage) is a type of mechanical linkage invented by James Watt in which the central moving point of the linkage is constrained to travel on a nearly straight line. It was described in ...
References
External links
* * * * {{DEFAULTSORT:Watt's Curve Sextic curvesCurve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...