voting system criterion

This article discusses the methods and results of comparing different electoral systems. There are two broad methods to compare voting systems:
# Metrics of voter satisfaction, either through simulation or survey.
# Adherence to logical criteria.

Evaluation by metrics

Models of the electoral process

Voting methods can be evaluated by measuring their accuracy under random simulated elections aiming to be faithful to the properties of elections in real life. The first such evaluation was conducted by Chamberlin and Cohen in 1978, who measured the frequency with which certain non-Condorcet systems elected Condorcet winners.

Condorcet jury model

The Marquis de Condorcet viewed elections as analogous to jury votes where each member expresses an independent judgement on the quality of candidates. Candidates differ in terms of their objective merit, but voters have imperfect information about the relative merits of the candidates. Such jury models are sometimes known as valence models. Condorcet and his contemporary Laplace demonstrated that, in such a model, voting theory could be reduced to probability by finding the expected quality of each candidate.

The jury model implies several natural concepts of accuracy for voting systems under different models:

# If voters' evaluations have errors following a normal distribution, the ideal procedure is score voting.
# If only ranking information is available, and there are many more voters than candidates, any Condorcet method will converge on a single Condorcet winner, who will have the highest probability of being the best candidate.

However, Condorcet's model is based on the extremely strong assumption of independent errors, i.e. voters will not be systematically biased in favor of one group of candidates or another. This is usually unrealistic: voters tend to communicate with each other, form parties or political ideologies, and engage in other behaviors that can result in correlated errors.

Black's spatial model

Duncan Black proposed a one-dimensional spatial model of voting in 1948, viewing elections as ideologically driven. His ideas were later expanded by Anthony Downs.Anthony Downs, " An Economic Theory of Democracy" (1957). Voters' opinions are regarded as positions in a space of one or more dimensions; candidates have positions in the same space; and voters choose candidates in order of proximity (measured under Euclidean distance or some other metric).

Spatial models imply a different notion of merit for voting systems: the more acceptable the winning candidate may be as a location parameter for the voter distribution, the better the system. A political spectrum is a one-dimensional spatial model.

Neutral models

Neutral voting models try to minimize the number of parameters and, as an example of the nothing-up-my-sleeve principle. The most common such model is the impartial anonymous culture model (or Dirichlet model). These models assume voters assign each candidate a utility completely at random (from a uniform distribution).

Comparisons of models

Tideman and Plassmann conducted a study which showed that a two-dimensional spatial model gave a reasonable fit to 3-candidate reductions of a large set of electoral rankings. Jury models, neutral models, and one-dimensional spatial models were all inadequate. They looked at Condorcet cycles in voter preferences (an example of which is A being preferred to B by a majority of voters, B to C and C to A) and found that the number of them was consistent with small-sample effects, concluding that "voting cycles will occur very rarely, if at all, in elections with many voters." The relevance of sample size had been studied previously by Gordon Tullock, who argued graphically that although finite electorates will be prone to cycles, the area in which candidates may give rise to cycling shrinks as the number of voters increases.

Utilitarian models

A utilitarian model views voters as ranking candidates in order of utility. The rightful winner, under this model, is the candidate who maximizes overall social utility. A utilitarian model differs from a spatial model in several important ways:
* It requires the additional assumption that voters are motivated solely by informed self-interest, with no ideological taint to their preferences.
* It requires the distance metric of a spatial model to be replaced by a faithful measure of utility.
* Consequently, the metric will need to differ between voters. It often happens that one group of voters will be powerfully affected by the choice between two candidates while another group has little at stake; the metric will then need to be highly asymmetric.
It follows from the last property that no voting system which gives equal influence to all voters is likely to achieve maximum social utility. Extreme cases of conflict between the claims of utilitarianism and democracy are referred to as the 'tyranny of the majority'. See Laslier's, Merlin's, and Nurmi's comments in Laslier's write-up.

James Mill seems to have been the first to claim the existence of an ''a priori'' connection between democracy and utilitarianism – see the Stanford Encyclopedia article.

Comparisons under a jury model

Suppose that the ''i ^th '' candidate in an election has merit ''x_i'' (we may assume that ''x_i'' ~ ''N'' (0,σ²)), and that voter ''j'' 's level of approval for candidate ''i'' may be written as ''x_i'' + ε_''ij'' (we will assume that the ε_''ij'' are iid. ''N'' (0,τ²)). We assume that a voter ranks candidates in decreasing order of approval. We may interpret ε_''ij'' as the error in voter ''j'' 's valuation of candidate ''i'' and regard a voting method as having the task of finding the candidate of greatest merit.

Each voter will rank the better of two candidates higher than the less good with a determinate probability ''p'' (which under the normal model outlined here is equal to $\tfrac\!+\!\tfrac\textrm^\tfrac$, as can be confirmed from a standard formula for Gaussian integrals over a quadrant).
Condorcet's jury theorem shows that so long as ''p'' > , the majority vote of a jury will be a better guide to the relative merits of two candidates than is the opinion of any single member.

Peyton Young showed that three further properties apply to votes between arbitrary numbers of candidates, suggesting that Condorcet was aware of the first and third of them.
* If ''p'' is close to , then the Borda winner is the maximum likelihood estimator of the best candidate.
* if ''p'' is close to 1, then the Minimax winner is the maximum likelihood estimator of the best candidate.
* For any ''p'', the Kemeny-Young ranking is the maximum likelihood estimator of the true order of merit.

Robert F. Bordley constructed a 'utilitarian' model which is a slight variant of Condorcet's jury model. He viewed the task of a voting method as that of finding the candidate who has the greatest total approval from the electorate, i.e. the highest sum of individual voters' levels of approval. This model makes sense even with σ² = 0, in which case ''p'' takes the value $\tfrac\!+\!\tfrac\textrm^\tfrac$ where ''n'' is the number of voters. He performed an evaluation under this model, finding as expected that the Borda count was most accurate.

Simulated elections under spatial models

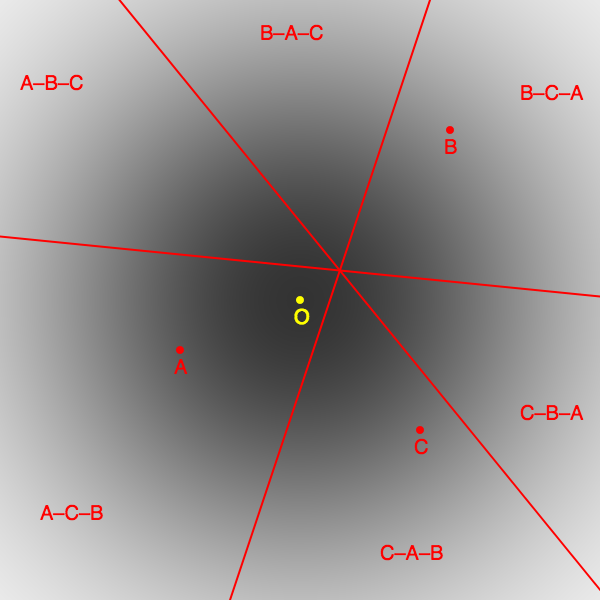
A simulated election can be constructed from a distribution of voters in a suitable space. The illustration shows voters satisfying a bivariate Gaussian distribution centred on O. There are 3 randomly generated candidates, A, B and C. The space is divided into 6 segments by 3 lines, with the voters in each segment having the same candidate preferences. The proportion of voters ordering the candidates in any way is given by the integral of the voter distribution over the associated segment.

The proportions corresponding to the 6 possible orderings of candidates determine the results yielded by different voting systems. Those which elect the best candidate, i.e. the candidate closest to O (who in this case is A), are considered to have given a correct result, and those which elect someone else have exhibited an error. By looking at results for large numbers of randomly generated candidates the empirical properties of voting systems can be measured.

The evaluation protocol outlined here is modelled on the one described by Tideman and Plassmann.
Evaluations of this type are commonest for single-winner electoral systems. Ranked voting systems fit most naturally into the framework, but other types of ballot (such a FPTP and Approval voting) can be accommodated with lesser or greater effort.

The evaluation protocol can be varied in a number of ways:
* The number of voters can be made finite and varied in size. In practice this is almost always done in multivariate models, with voters being sampled from their distribution and results for large electorates being used to show limiting behaviour.
* The number of candidates can be varied.
* The voter distribution could be varied; for instance, the effect of asymmetric distributions could be examined. A minor departure from normality is entailed by random sampling effects when the number of voters is finite. More systematic departures (seemingly taking the form of a Gaussian mixture model) were investigated by Jameson Quinn in 2017.

Evaluation for accuracy

One of the main uses of evaluations is to compare the accuracy of voting systems when voters vote sincerely. If an infinite number of voters satisfy a Gaussian distribution, then the rightful winner of an election can be taken to be the candidate closest to the mean/median, and the accuracy of a method can be identified with the proportion of elections in which the rightful winner is elected. The median voter theorem guarantees that all Condorcet systems will give 100% accuracy (and the same applies to Coombs' method).

Evaluations published in research papers use multidimensional Gaussians, making the calculation numerically difficult. The number of voters is kept finite and the number of candidates is necessarily small.

The computation is much more straightforward in a single dimension, which allows an infinite number of voters and an arbitrary number ''m'' of candidates. Results for this simple case are shown in the first table, which is directly comparable with Table 5 (1000 voters, medium dispersion) of the cited paper by Chamberlin and Cohen. The candidates were sampled randomly from the voter distribution and a single Condorcet method (Minimax) was included in the trials for confirmation.

The relatively poor performance of the Alternative vote (IRV) is explained by the well known and common source of error illustrated by the diagram, in which the election satisfies a univariate spatial model and the rightful winner B will be eliminated in the first round. A similar problem exists in all dimensions.

An alternative measure of accuracy is the average distance of voters from the winner (in which smaller means better). This is unlikely to change the ranking of voting methods, but is preferred by people who interpret distance as disutility. The second table shows the average distance (in standard deviations) ''minus'' $\sqrt\tfrac$ (which is the average distance of a variate from the centre of a standard Gaussian distribution) for 10 candidates under the same model.

Evaluation for resistance to tactical voting

James Green-Armytage et al. published a study in which they assessed the vulnerability of several voting systems to manipulation by voters. They say little about how they adapted their evaluation for this purpose, mentioning simply that it "requires creative programming". An earlier paper by the first author gives a little more detail.

The number of candidates in their simulated elections was limited to 3. This removes the distinction between certain systems; for instance Black's method and the Dasgupta-Maskin method are equivalent on 3 candidates.

The conclusions from the study are hard to summarise, but the Borda count performed badly; Minimax was somewhat vulnerable; and IRV was highly resistant. The authors showed that limiting any method to elections with no Condorcet winner (choosing the Condorcet winner when there was one) would never increase its susceptibility to tactical voting. They reported that the 'Condorcet-Hare' system which uses IRV as a tie-break for elections not resolved by the Condorcet criterion was as resistant to tactical voting as IRV on its own and more accurate. Condorcet-Hare is equivalent to Copeland's method with an IRV tie-break in elections with 3 candidates.

Evaluation for the effect of the candidate distribution

Some systems, and the Borda count in particular, are vulnerable when the distribution of candidates is displaced relative to the distribution of voters. The attached table shows the accuracy of the Borda count (as a percentage) when an infinite population of voters satisfies a univariate Gaussian distribution and ''m'' candidates are drawn from a similar distribution offset by ''x'' standard distributions. Red colouring indicates figures which are worse than random. Recall that all Condorcet methods give 100% accuracy for this problem. (And notice that the reduction in accuracy as ''x'' increases is not seen when there are only 3 candidates.)

Sensitivity to the distribution of candidates can be thought of as a matter either of accuracy or of resistance to manipulation. If one expects that in the course of things candidates will naturally come from the same distribution as voters, then any displacement will be seen as attempted subversion; but if one thinks that factors determining the viability of candidacy (such as financial backing) may be correlated with ideological position, then one will view it more in terms of accuracy.

Published evaluations take different views of the candidate distribution. Some simply assume that candidates are drawn from the same distribution as voters. Several older papers assume equal means but allow the candidate distribution to be more or less tight than the voter distribution. A paper by Tideman and Plassmann approximates the relationship between candidate and voter distributions based on empirical measurements. This is less realistic than it may appear, since it makes no allowance for the candidate distribution to adjust to exploit any weakness in the voting system. A paper by James Green-Armytage looks at the candidate distribution as a separate issue, viewing it as a form of manipulation and measuring the effects of strategic entry and exit. Unsurprisingly he finds the Borda count to be particularly vulnerable.

Evaluation for other properties

* As previously mentioned, Chamberlin and Cohen measured the frequency with which certain non-Condorcet systems elect Condorcet winners. Under a spatial model with equal voter and candidate distributions the frequencies are 99% ( Coombs), 86% (Borda), 60% (IRV) and 33% (FPTP). This is sometimes known as Condorcet efficiency.
* Darlington measured the frequency with which Copeland's method produces a unique winner in elections with no Condorcet winner. He found it to be less than 50% for fields of up to 10 candidates.

Experimental metrics

The task of a voting system under a spatial model is to identify the candidate whose position most accurately represents the distribution of voter opinions. This amounts to choosing a location parameter for the distribution from the set of alternatives offered by the candidates. Location parameters may be based on the mean, the median, or the mode; but since ranked preference ballots provide only ordinal information, the median is the only acceptable statistic.

This can be seen from the diagram, which illustrates two simulated elections with the same candidates but different voter distributions. In both cases the mid-point between the candidates is the 51st percentile of the voter distribution; hence 51% of voters prefer A and 49% prefer B. If we consider a voting method to be correct if it elects the candidate closest to the ''median'' of the voter population, then since the median is necessarily slightly to the left of the 51% line, a voting method will be considered to be correct if it elects A in each case.

The mean of the teal distribution is also slightly to the left of the 51% line, but the mean of the orange distribution is slightly to the right. Hence if we consider a voting method to be correct if it elects the candidate closest to the ''mean'' of the voter population, then a method will not be able to obtain full marks unless it produces different winners from the same ballots in the two elections. Clearly this will impute spurious errors to voting methods. The same problem will arise for any cardinal measure of location; only the median gives consistent results.

The median is not defined for multivariate distributions but the univariate median has a property which generalizes conveniently. The median of a distribution is the position whose average distance from all points within the distribution is smallest. This definition generalizes to the geometric median in multiple dimensions. The distance is often defined as a voter's disutility function.

If we have a set of candidates and a population of voters, then it is not necessary to solve the computationally difficult problem of finding the geometric median of the voters and then identify the candidate closest to it; instead we can identify the candidate whose average distance from the voters is minimized. This is the metric which has been generally deployed since Merrill onwards; see also Green-Armytage and Darlington.

The candidate closest to the geometric median of the voter distribution may be termed the 'spatial winner'.

Evaluation by real elections

Data from real elections can be analysed to compare the effects of different systems, either by comparing between countries or by applying alternative electoral systems to the real election data. The electoral outcomes can be compared through democracy indices, measures of political fragmentation, voter turnout, political efficacy and various economic and judicial indicators. The practical criteria to assess real elections include the share of wasted votes, the complexity of vote counting, proportionality of the representation elected based on parties' shares of votes, and barriers to entry for new political movements. Additional opportunities for comparison of real elections arise through electoral reforms.

A Canadian example of such an opportunity is seen in the City of Edmonton (Canada), which went from first-past-the-post voting in 1917 Alberta general election to five-member plurality block voting in 1921 Alberta general election, to five-member single transferable voting in 1926 Alberta general election, then to FPTP again in 1959 Alberta general election. One party swept all the Edmonton seats in 1917, 1921 and 1959. Under STV in 1926, two Conservatives, one Liberal, one Labour and one United Farmers MLA were elected.

Comparison of single-winner voting methods

Logical criteria for single-winner elections

Traditionally the merits of different electoral systems have been argued by reference to logical criteria. These have the form of rules of inference for electoral decisions, licensing the deduction, for instance, that "if ''E'' and ''E'' ' are elections such that ''R'' (''E'',''E'' '), and if ''A'' is the rightful winner of ''E'' , then ''A'' is the rightful winner of ''E'' ' ".

Result criteria (absolute)

The absolute criteria state that, if the set of ballots is a certain way, a certain candidate must or must not win.

Result criteria (relative)

These are criteria that state that, if a certain candidate wins in one circumstance, the same candidate must (or must not) win in a related circumstance.

Ballot-counting criteria

These are criteria which relate to the process of counting votes and determining a winner.

Strategy criteria

These are criteria that relate to a voter's incentive to use certain forms of strategy. They could also be considered as relative result criteria; however, unlike the criteria in that section, these criteria are directly relevant to voters; the fact that a method passes these criteria can simplify the process of figuring out one's optimal strategic vote.

Ballot format

Ballots are broadly distinguishable into two categories, cardinal and ordinal, where cardinal ballots request individual measures of support for each candidate and ordinal ballots request relative measures of support. A few methods do not fall neatly into one category, such as STAR, which asks the voter to give independent ratings for each candidate, but uses both the absolute and relative ratings to determine the winner. Comparing two methods based on ballot type alone is mostly a matter of voter experience preference, unless the ballot type is connected back to one of the other mathematical criterion listed here.

Relative strength

Criterion A is "stronger" than B if satisfying A implies satisfying B. For instance, the Condorcet criterion is stronger than the majority criterion, because all majority winners are Condorcet winners. Thus, any voting method that satisfies the Condorcet criterion must satisfy the majority criterion.

Compliance of selected single-winner methods

The following table shows which of the above criteria are met by several single-winner methods. Not every criterion is listed.

Practical factors

The concerns raised above are used by social choice theorists to devise systems that are accurate and resistant to manipulation. However, there are also practical reasons why one system may be more socially acceptable than another, which fall under the fields of public choice and political science. Important practical considerations include:
* Ease of explanation. Some voting rules are difficult to explain to voters in a way they can intuitively understand, which may undermine public trust in elections. For example, while Schulze's rule performs well by many of the criteria above, it requires an involved explanation of beatpaths.
* Ease of voting. Different kinds of ballots may be easier to fill out; for example, studies find that many voters consider ranked voting to be complex and confusing when compared to rated voting or X voting under first-past-the-post voting.

Other considerations include barriers to entry to the political competition and likelihood of gridlocked government. McGann, Anthony J., and Michael Latner. "The calculus of consensus democracy: Rethinking patterns of democracy without veto players." ''Comparative Political Studies'' 46.7 (2013): 823–850.

Comparison of multi-winner systems

Multi-winner electoral systems at their best seek to produce assemblies representative in a broader sense than that of making the same decisions as would be made by single-winner votes. They can also be route to one-party sweeps of a city's seats, if a non-proportional system, such as plurality block voting or ticket voting, is used.

Metrics for multi-winner evaluations

Evaluating the performance of multi-winner voting methods requires different metrics than are used for single-winner systems. The following have been proposed.
* Condorcet Committee Efficiency (CCE) measures the likelihood that a group of elected winners would beat all losers in pairwise races.
* The Gallagher Index and Loosemore–Hanby index (LH) measure proportionality between seat share and party vote share. Gallagher generally uses overall voting party percentages or votes compared to seat percentages to assess proportionality so ignores presence of districts if any.
* Wasted votes measure the fraction of electorate not represented by any representative.

Criterion tables

The following table shows which of the above criteria are met by several multiple winner methods.

See also

* Ranked voting
* Arrow's impossibility theorem
* Cardinal utility and ordinal utility
* Condorcet paradox

References

External links

*

{{Voting systems

Electoral system criteria