Vortex ring on:
[Wikipedia]
[Google]
[Amazon]
 A vortex ring, also called a toroidal vortex, is a
A vortex ring, also called a toroidal vortex, is a
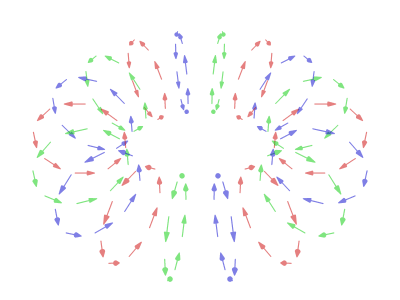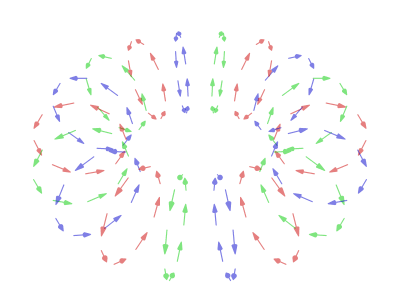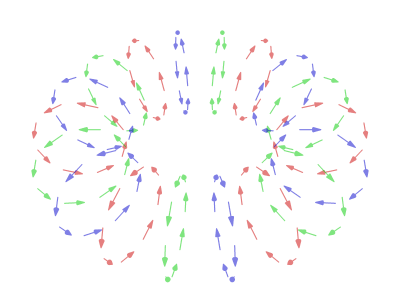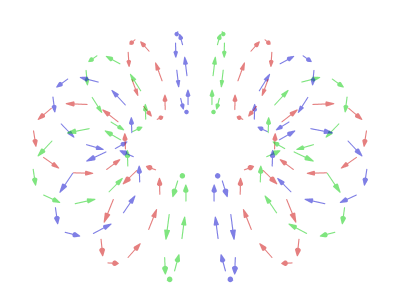 In a typical vortex ring, the fluid particles move in roughly circular paths around an imaginary circle (the ''core'') that is perpendicular to those paths. As in any vortex, the
In a typical vortex ring, the fluid particles move in roughly circular paths around an imaginary circle (the ''core'') that is perpendicular to those paths. As in any vortex, the
Physics Central, American Physical Society . Accessed January 2011.
 Air vortices can form around the main rotor of a
Air vortices can form around the main rotor of a
 Under particular conditions, some volcanic vents can produce large visible vortex rings. Though a rare phenomenon, several volcanoes have been observed emitting massive vortex rings as erupting steam and gas condense, forming visible toroidal clouds:
*
Under particular conditions, some volcanic vents can produce large visible vortex rings. Though a rare phenomenon, several volcanoes have been observed emitting massive vortex rings as erupting steam and gas condense, forming visible toroidal clouds:
*
 There has been research and experiments on the existence of separated vortex rings (SVR) such as those formed in the wake of the pappus of a
There has been research and experiments on the existence of separated vortex rings (SVR) such as those formed in the wake of the pappus of a
YouTube video of Vortex ring cannon
Fluid dynamics lecture covering vortices
Toy Box Physics: Vortices, Air Cannons, and Mushroom Clouds
Thesis on vortex ring formation and interactions
Vortex half-ring in a pool
Dianna Cowern (Physics Girl), YouTube
More experiments with vortex rings in a pool
Dianna Cowern (Physics Girl), YouTube {{DEFAULTSORT:Vortex Ring Aerodynamics Aviation risks Helicopter aerodynamics Vortices
 A vortex ring, also called a toroidal vortex, is a
A vortex ring, also called a toroidal vortex, is a torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
-shaped vortex
In fluid dynamics, a vortex (: vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in th ...
in a fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
; that is, a region where the fluid mostly spins around an imaginary axis line that forms a closed loop. The dominant flow in a vortex ring is said to be toroid
In mathematics, a toroid is a surface of revolution with a hole in the middle. The axis of revolution passes through the hole and so does not intersect the surface. For example, when a rectangle is rotated around an axis parallel to one of its ...
al, more precisely poloidal.
Vortex rings are plentiful in turbulent
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to laminar flow, which occurs when a fluid flows in parallel layers with no disruption between ...
flows of liquids and gases, but are rarely noticed unless the motion of the fluid is revealed by suspended particles—as in the smoke ring
A smoke ring is a visible vortex ring formed by smoke in a clear atmosphere.
Smoking, Smokers may blow smoke rings from the mouth, intentionally or accidentally. Smoke rings may also be formed by sudden bursts of fire (such as lighting and i ...
s which are often produced intentionally or accidentally by smokers. Fiery vortex rings are also a commonly produced trick by fire eaters. Visible vortex rings can also be formed by the firing of certain artillery
Artillery consists of ranged weapons that launch Ammunition, munitions far beyond the range and power of infantry firearms. Early artillery development focused on the ability to breach defensive walls and fortifications during sieges, and l ...
, in mushroom cloud
A mushroom cloud is a distinctive mushroom-shaped flammagenitus cloud of debris, smoke, and usually condensed water vapour resulting from a large explosion. The effect is most commonly associated with a nuclear explosion, but any sufficiently e ...
s, in microbursts, and rarely in volcanic eruptions.
A vortex ring usually tends to move in a direction that is perpendicular to the plane of the ring and such that the inner edge of the ring moves faster forward than the outer edge. Within a stationary body of fluid, a vortex ring can travel for relatively long distance, carrying the spinning fluid with it.
Structure
 In a typical vortex ring, the fluid particles move in roughly circular paths around an imaginary circle (the ''core'') that is perpendicular to those paths. As in any vortex, the
In a typical vortex ring, the fluid particles move in roughly circular paths around an imaginary circle (the ''core'') that is perpendicular to those paths. As in any vortex, the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
of the fluid is roughly constant except near the core, so that the angular velocity
In physics, angular velocity (symbol or \vec, the lowercase Greek letter omega), also known as the angular frequency vector,(UP1) is a pseudovector representation of how the angular position or orientation of an object changes with time, i ...
increases towards the core, and most of the vorticity
In continuum mechanics, vorticity is a pseudovector (or axial vector) field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point an ...
(and hence most of the energy dissipation) is concentrated near it.
Unlike a sea wave, whose motion is only apparent, a moving vortex ring actually carries the spinning fluid along. Just as a rotating wheel lessens friction between a car and the ground, the poloidal flow of the vortex lessens the friction between the core and the surrounding stationary fluid, allowing it to travel a long distance with relatively little loss of mass and kinetic energy, and little change in size or shape. Thus, a vortex ring can carry mass much further and with less dispersion than a jet of fluid. That explains, for instance, why a smoke ring keeps traveling long after any extra smoke blown out with it has stopped and dispersed. These properties of vortex rings are exploited in the vortex ring gun for riot control, and vortex ring toys such as the air vortex cannons.Physics in a Toroidal Vortex: Air CannonPhysics Central, American Physical Society . Accessed January 2011.
Formation
Formation process
The formation of vortex rings has fascinated the scientific community for more than a century, starting withWilliam Barton Rogers
William Barton Rogers (December 7, 1804 – May 30, 1882) was an American geologist, physicist, and the founder and first president of the Massachusetts Institute of Technology (MIT).
An acclaimed lecturer in the physical sciences, Rogers taug ...
who made sounding observations of the formation process of air vortex rings in air, air rings in liquids, and liquid rings in liquids. In particular, William Barton Rogers
William Barton Rogers (December 7, 1804 – May 30, 1882) was an American geologist, physicist, and the founder and first president of the Massachusetts Institute of Technology (MIT).
An acclaimed lecturer in the physical sciences, Rogers taug ...
made use of the simple experimental method of letting a drop of liquid fall on a free liquid surface; a falling colored drop of liquid, such as milk or dyed water, will inevitably form a vortex ring at the interface due to the surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
.
A method proposed by G. I. Taylor
Sir Geoffrey Ingram Taylor Order of Merit, OM Royal Society of London, FRS FRSE (7 March 1886 – 27 June 1975) was a British physicist and mathematician, who made contributions to fluid dynamics and wave theory.
Early life and education
Tayl ...
to generate a vortex ring is to impulsively start a disk from rest. The flow separates to form a cylindrical vortex sheet and by artificially dissolving the disk, one is left with an isolated vortex ring. This is the case when someone is stirring their cup of coffee with a spoon and observing the propagation of a half-vortex in the cup.
In a laboratory, vortex rings are formed by impulsively discharging fluid through a sharp-edged nozzle or orifice. The impulsive motion of the piston/cylinder system is either triggered by an electric actuator or by a pressurized vessel connected to a control valve. For a nozzle geometry, and at first approximation, the exhaust speed is uniform and equal to the piston speed. This is referred as a parallel starting jet. It is possible to have a conical nozzle in which the streamlines at the exhaust are directed toward the centerline. This is referred as a converging starting jet. The orifice geometry which consists in an orifice plate covering the straight tube exhaust, can be considered as an infinitely converging nozzle but the vortex formation differs considerably from the converging nozzle, principally due to the absence of boundary layer in the thickness of the orifice plate throughout the formation process. The fast moving fluid (A) is therefore discharged into a quiescent fluid (B). The shear imposed at the interface between the two fluids slows down the outer layer of the fluid (A) relatively to the centerline fluid. In order to satisfy the Kutta condition, the flow is forced to detach, curl and roll-up in the form of a vortex sheet. Later, the vortex sheet detaches from the feeding jet and propagates freely downstream due to its self-induced kinematics. This is the process commonly observed when a smoker forms smoke rings from their mouth, and how vortex ring toys work.
Secondary effects are likely to modify the formation process of vortex rings. Firstly, at the very first instants, the velocity profile at the exhaust exhibits extrema near the edge causing a large vorticity flux into the vortex ring. Secondly, as the ring grows in size at the edge of the exhaust, negative vorticity is generated on the outer wall of the generator which considerably reduces the circulation accumulated by the primary ring. Thirdly, as the boundary layer inside the pipe, or nozzle, thickens, the velocity profile approaches the one of a Poiseuille flow and the centerline velocity at the exhaust is measured to be larger than the prescribed piston speed. Last but not least, in the event the piston-generated vortex ring is pushed through the exhaust, it may interact or even merge with the primary vortex, hence modifying its characteristic, such as circulation, and potentially forcing the transition of the vortex ring to turbulence.
Vortex ring structures are easily observable in nature. For instance, a mushroom cloud
A mushroom cloud is a distinctive mushroom-shaped flammagenitus cloud of debris, smoke, and usually condensed water vapour resulting from a large explosion. The effect is most commonly associated with a nuclear explosion, but any sufficiently e ...
formed by a nuclear explosion or volcanic eruption, has a vortex ring-like structure. Vortex rings are also seen in many different biological flows; blood is discharged into the left ventricle of the human heart in the form of a vortex ring and jellyfishes or squids were shown to propel themselves in water by periodically discharging vortex rings in the surrounding. Finally, for more industrial applications, the synthetic jet which consists in periodically-formed vortex rings, was proved to be an appealing technology for flow control, heat and mass transfer and thrust generation
Vortex formation number
Prior to Gharib ''et al.'' (1998), few studies had focused on the formation of vortex rings generated with long stroke-to-diameter ratios , where is the length of the column of fluid discharged through the exhaust and is the diameter of the exhaust. For short stroke ratios, only one isolated vortex ring is generated and no fluid is left behind in the formation process. For long stroke ratios, however, the vortex ring is followed by some energetic fluid, referred as the trailing jet. On top of showing experimental evidence of the phenomenon, an explanation of the phenomenon was provided in terms of energy maximisation invoking a variational principle first reported byKelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By de ...
and later proven by Benjamin (1976), or Friedman & Turkington (1981). Ultimately, Gharib ''et al.'' (1998) observed the transition between these two states to occur at a non-dimensional time , or equivalently a stroke ratio , of about 4. The robustness of this number with respect to initial and boundary conditions suggested the quantity to be a universal constant and was thus named ''formation number''.
The phenomenon of 'pinch-off', or detachment, from the feeding starting jet is observed in a wide range of flows observed in nature. For instance, it was shown that biological systems such as the human heart or swimming and flying animals generate vortex rings with a stroke-to-diameter ratio close to the formation number of about 4, hence giving ground to the existence of an optimal vortex ring formation process in terms of propulsion, thrust generation and mass transport. In particular, the squid '' lolliguncula brevis'' was shown to propel itself by periodically emitting vortex rings at a stroke-ratio close to 4. Moreover, in another study by Gharib ''et al'' (2006), the formation number was used as an indicator to monitor the health of the human heart and identify patients with dilated cardiomyopathy
Dilated cardiomyopathy (DCM) is a condition in which the heart becomes enlarged and cannot pump blood effectively. Symptoms vary from none to feeling tired, leg swelling, and shortness of breath. It may also result in chest pain or fainting. C ...
.
Other examples
Vortex ring state in helicopters
 Air vortices can form around the main rotor of a
Air vortices can form around the main rotor of a helicopter
A helicopter is a type of rotorcraft in which Lift (force), lift and thrust are supplied by horizontally spinning Helicopter rotor, rotors. This allows the helicopter to VTOL, take off and land vertically, to hover (helicopter), hover, and ...
, causing a dangerous condition known as vortex ring state (VRS) or "settling with power". In this condition, air that moves down through the rotor turns outward, then up, inward, and then down through the rotor again. This re-circulation of flow can negate much of the lifting force and cause a catastrophic loss of altitude. Applying more power (increasing collective pitch) serves to further accelerate the downwash through which the main-rotor is descending, exacerbating the condition.
In the human heart
A vortex ring is formed in the left ventricle of thehuman heart
The heart is a muscular organ found in humans and other animals. This organ pumps blood through the blood vessels. The heart and blood vessels together make the circulatory system. The pumped blood carries oxygen and nutrients to the tiss ...
during cardiac relaxation (diastole
Diastole ( ) is the relaxed phase of the cardiac cycle when the chambers of the heart are refilling with blood. The contrasting phase is systole when the heart chambers are contracting. Atrial diastole is the relaxing of the atria, and ventricul ...
), as a jet of blood
Blood is a body fluid in the circulatory system of humans and other vertebrates that delivers necessary substances such as nutrients and oxygen to the cells, and transports metabolic waste products away from those same cells.
Blood is com ...
enters through the mitral valve
The mitral valve ( ), also known as the bicuspid valve or left atrioventricular valve, is one of the four heart valves. It has two Cusps of heart valves, cusps or flaps and lies between the atrium (heart), left atrium and the ventricle (heart), ...
. This phenomenon was initially observed in vitro
''In vitro'' (meaning ''in glass'', or ''in the glass'') Research, studies are performed with Cell (biology), cells or biological molecules outside their normal biological context. Colloquially called "test-tube experiments", these studies in ...
and subsequently strengthened by analyses based on color Doppler mapping and magnetic resonance imaging
Magnetic resonance imaging (MRI) is a medical imaging technique used in radiology to generate pictures of the anatomy and the physiological processes inside the body. MRI scanners use strong magnetic fields, magnetic field gradients, and ...
. Some recent studies have also confirmed the presence of a vortex ring during rapid filling phase of diastole
Diastole ( ) is the relaxed phase of the cardiac cycle when the chambers of the heart are refilling with blood. The contrasting phase is systole when the heart chambers are contracting. Atrial diastole is the relaxing of the atria, and ventricul ...
and implied that the process of vortex ring formation can influence mitral annulus dynamics.
Bubble rings
Releasing air underwater formsbubble ring
A bubble ring, or toroidal bubble, is an underwater vortex ring where an air bubble occupies the core of the vortex, forming a ring shape. The ring of air as well as the nearby water spins Toroidal and poloidal, poloidally as it travels through ...
s, which are vortex rings of water with bubbles (or even a single donut-shaped bubble) trapped along its axis line. Such rings are often produced by scuba divers and dolphin
A dolphin is an aquatic mammal in the cetacean clade Odontoceti (toothed whale). Dolphins belong to the families Delphinidae (the oceanic dolphins), Platanistidae (the Indian river dolphins), Iniidae (the New World river dolphins), Pontopori ...
s.
Volcanoes
 Under particular conditions, some volcanic vents can produce large visible vortex rings. Though a rare phenomenon, several volcanoes have been observed emitting massive vortex rings as erupting steam and gas condense, forming visible toroidal clouds:
*
Under particular conditions, some volcanic vents can produce large visible vortex rings. Though a rare phenomenon, several volcanoes have been observed emitting massive vortex rings as erupting steam and gas condense, forming visible toroidal clouds:
*Mount Etna
Mount Etna, or simply Etna ( or ; , or ; ; or ), is an active stratovolcano on the east coast of Sicily, Italy, in the Metropolitan City of Catania, between the cities of Messina, Italy, Messina and Catania. It is located above the Conve ...
, Italy (Sicily
Sicily (Italian language, Italian and ), officially the Sicilian Region (), is an island in the central Mediterranean Sea, south of the Italian Peninsula in continental Europe and is one of the 20 regions of Italy, regions of Italy. With 4. ...
)
* Stromboli, Italy (Aeolian Islands
The Aeolian Islands ( ; ; ), sometimes referred to as the Lipari Islands or Lipari group ( , ) after their largest island, are a volcanic archipelago in the Tyrrhenian Sea north of Sicily, said to be named after Aeolus, the mythical ruler of ...
)
*Eyjafjallajökull
Eyjafjallajökull (; "glacier of (the mountain) Eyjafjöll"), sometimes referred to by the numeronym E15, is one of the smaller ice caps of Iceland, north of Skógar and west of Mýrdalsjökull. The ice cap covers the caldera of a volcano wi ...
, Iceland
Iceland is a Nordic countries, Nordic island country between the Atlantic Ocean, North Atlantic and Arctic Oceans, on the Mid-Atlantic Ridge between North America and Europe. It is culturally and politically linked with Europe and is the regi ...
*Hekla
Hekla (), or Hecla, is an active stratovolcano in the south of Iceland with a height of . Hekla is one of Iceland's most active volcanoes; over 20 eruptions have occurred in and around the volcano since the year 1210. During the Middle Ages, th ...
, Iceland
Iceland is a Nordic countries, Nordic island country between the Atlantic Ocean, North Atlantic and Arctic Oceans, on the Mid-Atlantic Ridge between North America and Europe. It is culturally and politically linked with Europe and is the regi ...
*Tungurahua
Tungurahua (; from Quichua ''tunguri'' (throat) and ''rahua'' (fire), "Throat of Fire")) is an active stratovolcano located in the Cordillera Oriental of Ecuador. The volcano gives its name to the province of Tungurahua. Volcanic activity re ...
, Ecuador
Ecuador, officially the Republic of Ecuador, is a country in northwestern South America, bordered by Colombia on the north, Peru on the east and south, and the Pacific Ocean on the west. It also includes the Galápagos Province which contain ...
* Pacaya, Guatemala
Guatemala, officially the Republic of Guatemala, is a country in Central America. It is bordered to the north and west by Mexico, to the northeast by Belize, to the east by Honduras, and to the southeast by El Salvador. It is hydrologically b ...
* Mount Redoubt, United States (Alaska
Alaska ( ) is a non-contiguous U.S. state on the northwest extremity of North America. Part of the Western United States region, it is one of the two non-contiguous U.S. states, alongside Hawaii. Alaska is also considered to be the north ...
)
* Mount Aso, Japan (Kyushu
is the third-largest island of Japan's Japanese archipelago, four main islands and the most southerly of the four largest islands (i.e. excluding Okinawa Island, Okinawa and the other Ryukyu Islands, Ryukyu (''Nansei'') Ryukyu Islands, Islands ...
)
* Whakaari (White Island), New Zealand
* Gunung Slamet, Indonesia
Indonesia, officially the Republic of Indonesia, is a country in Southeast Asia and Oceania, between the Indian Ocean, Indian and Pacific Ocean, Pacific oceans. Comprising over List of islands of Indonesia, 17,000 islands, including Sumatra, ...
(Central Java
Central Java (, ) is a Provinces of Indonesia, province of Indonesia, located in the middle of the island of Java. Its administrative capital is Semarang. It is bordered by West Java in the west, the Indian Ocean and the Special Region of Yogya ...
)
* Momotombo, Nicaragua
Nicaragua, officially the Republic of Nicaragua, is the geographically largest Sovereign state, country in Central America, comprising . With a population of 7,142,529 as of 2024, it is the third-most populous country in Central America aft ...
( León)
Separated vortex rings
 There has been research and experiments on the existence of separated vortex rings (SVR) such as those formed in the wake of the pappus of a
There has been research and experiments on the existence of separated vortex rings (SVR) such as those formed in the wake of the pappus of a dandelion
''Taraxacum'' () is a genus of flowering plants in the family Asteraceae, which consists of species commonly known as dandelions. The scientific and hobby study of the genus is known as taraxacology. The genus has a near-cosmopolitan distribu ...
. This special type of vortex ring effectively stabilizes the seed as it travels through the air and increases the lift generated by the seed. Compared to a standard vortex ring, which is propelled downstream, the axially symmetric SVR remains attached to the pappus for the duration of its flight and uses drag to enhance the travel. These dandelion seed structures have been used to create tiny battery-free wireless sensors that can float in the wind and be dispersed across a large area.
Theory
Historical studies
The formation of vortex rings has fascinated the scientific community for more than a century, starting withWilliam Barton Rogers
William Barton Rogers (December 7, 1804 – May 30, 1882) was an American geologist, physicist, and the founder and first president of the Massachusetts Institute of Technology (MIT).
An acclaimed lecturer in the physical sciences, Rogers taug ...
who made sounding observations of the formation process of air vortex rings in air, air rings in liquids, and liquid rings in liquids. In particular, William Barton Rogers
William Barton Rogers (December 7, 1804 – May 30, 1882) was an American geologist, physicist, and the founder and first president of the Massachusetts Institute of Technology (MIT).
An acclaimed lecturer in the physical sciences, Rogers taug ...
made use of the simple experimental method of letting a drop of liquid fall on a free liquid surface; a falling colored drop of liquid, such as milk or dyed water, will inevitably form a vortex ring at the interface due to the surface tension.
Vortex rings were first mathematically analyzed by the German physicist Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz (; ; 31 August 1821 – 8 September 1894; "von" since 1883) was a German physicist and physician who made significant contributions in several scientific fields, particularly hydrodynamic stability. The ...
, in his 1858 paper ''On Integrals of the Hydrodynamical Equations which Express Vortex-motion''.
Circular vortex lines
For a single zero-thickness vortex ring, the vorticity is represented by aDirac delta function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line ...
as where denotes the coordinates of the vortex filament of strength in a constant half-plane. The Stokes stream function
In fluid dynamics, the Stokes stream function is used to describe the Streamlines, streaklines, and pathlines, streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes ...
is:
with
where and are respectively the least and the greatest distance from the point to the vortex line, and where is the complete elliptic integral of the first kind
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Carlo de' Toschi di Fagnano, Giulio Fagnano and Leonhard Euler (). Their name originat ...
and is the complete elliptic integral of the second kind.
A circular vortex line is the limiting case of a thin vortex ring. Because there is no core thickness, the speed of the ring is infinite, as well as the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
. The hydrodynamic impulse can be expressed in term of the strength, or 'circulation' , of the vortex ring as .
Thin-core vortex rings
The discontinuity introduced by theDirac delta function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line ...
prevents the computation of the speed and the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
of a circular vortex line. It is however possible to estimate these quantities for a vortex ring having a finite small thickness. For a thin vortex ring, the core can be approximated by a disk of radius which is assumed to be infinitesimal compared to the radius of the ring , i.e. . As a consequence, inside and in the vicinity of the core ring, one may write: , and , and, in the limit of , the elliptic integrals can be approximated by and .
For a uniform vorticity
In continuum mechanics, vorticity is a pseudovector (or axial vector) field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point an ...
distribution in the disk, the Stokes stream function
In fluid dynamics, the Stokes stream function is used to describe the Streamlines, streaklines, and pathlines, streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes ...
can therefore be approximated by
The resulting circulation , hydrodynamic impulse and kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
are
It is also possible to find the translational ring speed (which is finite) of such isolated thin-core vortex ring:
which finally results in the well-known expression found by Kelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By de ...
and published in the English translation by Tait of von Helmholtz's paper:
Spherical vortices
Hill
A hill is a landform that extends above the surrounding terrain. It often has a distinct summit, and is usually applied to peaks which are above elevation compared to the relative landmass, though not as prominent as Mountain, mountains. Hills ...
's spherical vortex is an example of steady vortex flow and may be used to model vortex rings having a vorticity distribution extending to the centerline. More precisely, the model supposes a linearly distributed vorticity distribution in the radial direction starting from the centerline and bounded by a sphere of radius as:
where is the constant translational speed of the vortex.
Finally, the Stokes stream function
In fluid dynamics, the Stokes stream function is used to describe the Streamlines, streaklines, and pathlines, streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes ...
of Hill's spherical vortex can be computed and is given by:
The above expressions correspond to the stream function describing a steady flow. In a fixed frame of reference, the stream function of the bulk flow having a speed should be added.
The circulation, the hydrodynamic impulse and the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
can also be calculated in terms of the translational speed and radius :
Such a structure or an electromagnetic equivalent has been suggested as an explanation for the internal structure of ball lightning
Ball lightning is a rare and unexplained phenomenon described as Luminosity, luminescent, spherical objects that vary from pea-sized to several meters in diameter. Though usually associated with thunderstorms, the observed phenomenon is repor ...
. For example, Shafranov used a magnetohydrodynamic (MHD) analogy to Hill's stationary fluid mechanical vortex to consider the equilibrium conditions of axially symmetric MHD configurations, reducing the problem to the theory of stationary flow of an incompressible fluid. In axial symmetry, he considered general equilibrium for distributed currents and concluded under the Virial Theorem
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by a conservative force (where the work done is independent of path), with ...
that if there were no gravitation, a bounded equilibrium configuration could exist only in the presence of an azimuthal current.
Fraenkel-Norbury model
The Fraenkel-Norbury model of isolated vortex ring, sometimes referred as the standard model, refers to the class of steady vortex rings having a linear distribution of vorticity in the core and parametrised by the mean core radius , where is the area of the vortex core and is the radius of the ring. Approximate solutions were found for thin-core rings, i.e. , and thick Hill's-like vortex rings, i.e. , Hill's spherical vortex having a mean core radius of precisely . For mean core radii in between, one must rely on numerical methods. Norbury (1973) found numerically the resulting steady vortex ring of given mean core radius, and this for a set of 14 mean core radii ranging from 0.1 to 1.35. The resulting streamlines defining the core of the ring were tabulated, as well as the translational speed. In addition, the circulation, the hydrodynamic impulse and the kinetic energy of such steady vortex rings were computed and presented in non-dimensional form.Instabilities
A kind of azimuthal radiant-symmetric structure was observed by Maxworthy when the vortex ring traveled around a critical velocity, which is between the turbulence and laminar states. Later Huang and ChanHuang, J., Chan, K.T. (2007) ''Dual-Wavelike Instability in Vortex Rings'', Proc. 5th IASME/WSEAS Int. Conf. Fluid Mech. & Aerodyn., Greece reported that if the initial state of the vortex ring is not perfectly circular, another kind of instability would occur. An elliptical vortex ring undergoes an oscillation in which it is first stretched in the vertical direction and squeezed in the horizontal direction, then passes through an intermediate state where it is circular, then is deformed in the opposite way (stretched in the horizontal direction and squeezed in the vertical) before reversing the process and returning to the original state.See also
* Air vortex cannon *Bubble ring
A bubble ring, or toroidal bubble, is an underwater vortex ring where an air bubble occupies the core of the vortex, forming a ring shape. The ring of air as well as the nearby water spins Toroidal and poloidal, poloidally as it travels through ...
– underwater vortex ring
* Mushroom cloud
A mushroom cloud is a distinctive mushroom-shaped flammagenitus cloud of debris, smoke, and usually condensed water vapour resulting from a large explosion. The effect is most commonly associated with a nuclear explosion, but any sufficiently e ...
* Toroidal moment
* Vortex ring gun
* Vortex ring toy
References
External links
YouTube video of Vortex ring cannon
Fluid dynamics lecture covering vortices
Toy Box Physics: Vortices, Air Cannons, and Mushroom Clouds
Thesis on vortex ring formation and interactions
Vortex half-ring in a pool
Dianna Cowern (Physics Girl), YouTube
More experiments with vortex rings in a pool
Dianna Cowern (Physics Girl), YouTube {{DEFAULTSORT:Vortex Ring Aerodynamics Aviation risks Helicopter aerodynamics Vortices