vibration spectrum

A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 10¹³  Hz to approximately 10¹⁴ Hz, corresponding to wavenumbers of approximately 300 to 3000 cm⁻¹ and wavelengths of approximately 30 to 3 μm.

Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of parts of the molecule. In general, a non-linear molecule with ''N'' atoms has normal modes of vibration, but a ''linear'' molecule has modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond.

A molecular vibration is excited when the molecule absorbs energy, Δ''E'', corresponding to the vibration's frequency, ''ν'', according to the relation , where ''h'' is the Planck constant. A fundamental vibration is evoked when one such quantum of energy is absorbed by the molecule in its ground state. When multiple quanta are absorbed, the first and possibly higher overtones are excited.

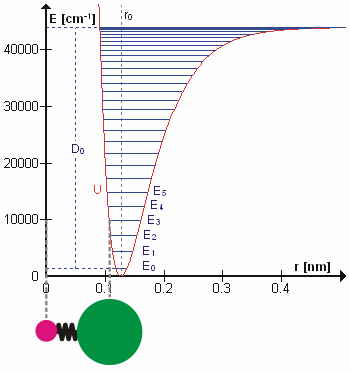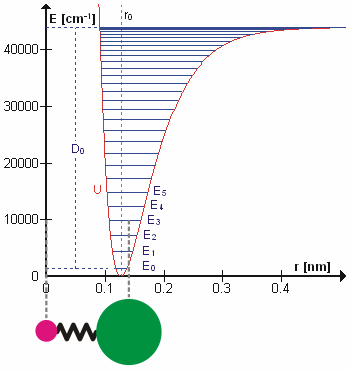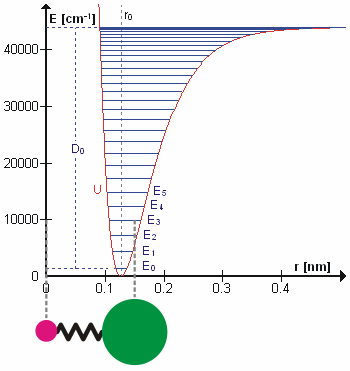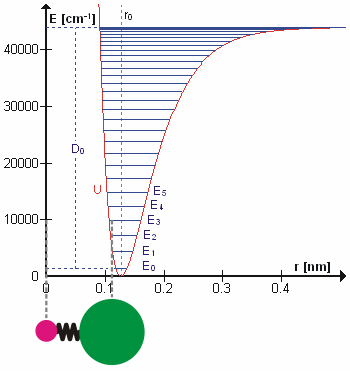
To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone has twice the frequency of the fundamental. In reality, vibrations are anharmonic and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, because the potential energy of the molecule is more like a Morse potential or more accurately, a Morse/Long-range potential.

The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy, which typically uses visible light, can also be used to measure vibration frequencies directly. The two techniques are complementary and comparison between the two can provide useful structural information such as in the case of the rule of mutual exclusion for centrosymmetric molecules.

Vibrational excitation can occur in conjunction with electronic excitation in the ultraviolet-visible region. The combined excitation is known as a vibronic transition, giving vibrational fine structure to electronic transitions, particularly for molecules in the gas state.

Simultaneous excitation of a vibration and rotations gives rise to vibration–rotation spectra.

Number of vibrational modes

For a molecule with atoms, the positions of all nuclei depend on a total of 3 coordinates, so that the molecule has 3 degrees of freedom including translation, rotation and vibration. Translation corresponds to movement of the center of mass whose position can be described by 3 cartesian coordinates.

A nonlinear molecule can rotate about any of three mutually perpendicular axes and therefore has 3 rotational degrees of freedom. For a linear molecule, rotation about the molecular axis does not involve movement of any atomic nucleus, so there are only 2 rotational degrees of freedom which can vary the atomic coordinates.

An equivalent argument is that the rotation of a linear molecule changes the direction of the molecular axis in space, which can be described by 2 coordinates corresponding to latitude and longitude. For a nonlinear molecule, the direction of one axis is described by these two coordinates, and the orientation of the molecule about this axis provides a third rotational coordinate.

The number of vibrational modes is therefore 3 minus the number of translational and rotational degrees of freedom, or for linear and for nonlinear molecules.

Vibrational coordinates

The coordinate of a normal vibration is a combination of ''changes'' in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency , the frequency of the vibration.

Internal coordinates

''Internal coordinates'' are of the following types, illustrated with reference to the planar molecule ethylene,
* Stretching: a change in the length of a bond, such as C–H or C–C
* Bending: a change in the angle between two bonds, such as the HCH angle in a methylene group
* Rocking: a change in angle between a group of atoms, such as a methylene group and the rest of the molecule
* Wagging: a change in angle between the plane of a group of atoms, such as a methylene group and a plane through the rest of the molecule
* Twisting: a change in the angle between the planes of two groups of atoms, such as a change in the angle between the two methylene groups
* Out-of-plane: a change in the angle between any one of the C–H bonds and the plane defined by the remaining atoms of the ethylene molecule. Another example is in BF₃ when the boron atom moves in and out of the plane of the three fluorine atoms.

In a rocking, wagging or twisting coordinate the bond lengths within the groups involved do not change. The angles do. Rocking is distinguished from wagging by the fact that the atoms in the group stay in the same plane.

In ethylene there are 12 internal coordinates: 4 C–H stretching, 1 C–C stretching, 2 H–C–H bending, 2 CH₂ rocking, 2 CH₂ wagging, 1 twisting. Note that the H–C–C angles cannot be used as internal coordinates as well as the H–C–H angle because the angles at each carbon atom cannot all increase at the same time.

Note that these coordinates do not correspond to normal modes (see '). In other words, they do not correspond to particular frequencies or vibrational transitions.

Vibrations of a methylene group (−CH₂−) in a molecule for illustration

Within the CH₂ group, commonly found in organic compounds, the two low mass hydrogens can vibrate in six different ways which can be grouped as 3 pairs of modes: 1. symmetric and asymmetric stretching, 2. scissoring and rocking, 3. wagging and twisting. These are shown here:

(These figures do not represent the "recoil" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).

Symmetry-adapted coordinates

Symmetry–adapted coordinates may be created by applying a projection operator to a set of internal coordinates. The projection operator is constructed with the aid of the character table of the molecular point group. For example, the four (un-normalized) C–H stretching coordinates of the molecule ethene are given by
$\begin Q_ &= q_ + q_ + q_ + q_ \\ Q_ &= q_ + q_ - q_ - q_ \\ Q_ &= q_ - q_ + q_ - q_ \\ Q_ &= q_ - q_ - q_ + q_ \end$
where $q_ - q_$ are the internal coordinates for stretching of each of the four C–H bonds.

Illustrations of symmetry–adapted coordinates for most small molecules can be found in Nakamoto.

Normal coordinates

The normal coordinates, denoted as ''Q'', refer to the positions of atoms away from their equilibrium positions, with respect to a normal mode of vibration. Each normal mode is assigned a single normal coordinate, and so the normal coordinate refers to the "progress" along that normal mode at any given time. Formally, normal modes are determined by solving a secular determinant, and then the normal coordinates (over the normal modes) can be expressed as a summation over the cartesian coordinates (over the atom positions). The normal modes diagonalize the matrix governing the molecular vibrations, so that each normal mode is an independent molecular vibration. If the molecule possesses symmetries, the normal modes "transform as" an irreducible representation under its point group. The normal modes are determined by applying group theory, and projecting the irreducible representation onto the cartesian coordinates. For example, when this treatment is applied to CO₂, it is found that the C=O stretches are not independent, but rather there is an O=C=O symmetric stretch and an O=C=O asymmetric stretch:
* symmetric stretching: the sum of the two C–O stretching coordinates; the two C–O bond lengths change by the same amount and the carbon atom is stationary.
* asymmetric stretching: the difference of the two C–O stretching coordinates; one C–O bond length increases while the other decreases.

When two or more normal coordinates belong to the same irreducible representation of the molecular point group (colloquially, have the same symmetry) there is "mixing" and the coefficients of the combination cannot be determined ''a priori''. For example, in the linear molecule hydrogen cyanide, HCN, The two stretching vibrations are
* principally C–H stretching with a little C–N stretching;
* principally C–N stretching with a little C–H stretching;
The coefficients a and b are found by performing a full normal coordinate analysis by means of the Wilson GF method.

Newtonian mechanics

Perhaps surprisingly, molecular vibrations can be treated using Newtonian mechanics to calculate the correct vibration frequencies. The basic assumption is that each vibration can be treated as though it corresponds to a spring. In the harmonic approximation the spring obeys Hooke's law: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a ''force constant, k''. The anharmonic oscillator is considered elsewhere.
$\mathrm = - k Q$
By Newton's second law of motion this force is also equal to a reduced mass, ''μ'', times acceleration.
$\mathrm = \mu \frac$
Since this is one and the same force the ordinary differential equation follows.
$\mu \frac + k Q = 0$
The solution to this equation of simple harmonic motion is
$Q(t) = A \cos (2 \pi \nu t) ;\ \ \nu = \sqrt.$
''A'' is the maximum amplitude of the vibration coordinate ''Q''. It remains to define the reduced mass, ''μ''. In general, the reduced mass of a diatomic molecule, AB, is expressed in terms of the atomic masses, ''m_A'' and ''m_B'', as
$\frac = \frac+\frac.$
The use of the reduced mass ensures that the centre of mass of the molecule is not affected by the vibration. In the harmonic approximation the potential energy of the molecule is a quadratic function of the normal coordinate. It follows that the force-constant is equal to the second derivative of the potential energy.
$k=\frac$

When two or more normal vibrations have the same symmetry a full normal coordinate analysis must be performed (see GF method). The vibration frequencies, ''ν''_''i'', are obtained from the eigenvalues, ''λ''_''i'', of the matrix product ''GF''. ''G'' is a matrix of numbers derived from the masses of the atoms and the geometry of the molecule. ''F'' is a matrix derived from force-constant values. Details concerning the determination of the eigenvalues can be found in.

Quantum mechanics

In the harmonic approximation the potential energy is a quadratic function of the normal coordinates. Solving the Schrödinger wave equation, the energy states for each normal coordinate are given by
$E_n = h \left( n + \right)\nu=h\left( n + \right) \sqrt ,$
where ''n'' is a quantum number that can take values of 0, 1, 2, ... In molecular spectroscopy where several types of molecular energy are studied and several quantum numbers are used, this ''vibrational quantum number'' is often designated as ''v''.

The difference in energy when ''n'' (or ''v'') changes by 1 is therefore equal to $h\nu$, the product of the Planck constant and the vibration frequency derived using classical mechanics. For a transition from level ''n'' to level ''n+1'' due to absorption of a photon, the frequency of the photon is equal to the classical vibration frequency $\nu$ (in the harmonic oscillator approximation).

See quantum harmonic oscillator for graphs of the first 5 wave functions, which allow certain selection rules to be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number ''n'' changes by one,
$\Delta n = \pm 1$but this does not apply to an anharmonic oscillator; the observation of overtones is only possible because vibrations are anharmonic. Another consequence of anharmonicity is that transitions such as between states and have slightly less energy than transitions between the ground state and first excited state. Such a transition gives rise to a hot band. To describe vibrational levels of an anharmonic oscillator, Dunham expansion is used.

When it comes to polyatomic molecules, it is common to solve the Schrödinger Equation using Watson's nuclear motion Hamiltonian. Similar as for diatomics, this can be done within the harmonic approximation as stated above. For the anharmonic calculation of vibrational spectra of polyatomic molecules, more sophisticated approaches are used. Prominent examples in computational chemistry are 2nd order vibrational perturbation theory (VPT2) or vibrational configuration interaction theory (VCI).

Intensities

In an infrared spectrum the intensity of an absorption band is proportional to the derivative of the molecular dipole moment with respect to the normal coordinate. Likewise, the intensity of Raman bands depends on the derivative of polarizability with respect to the normal coordinate. There is also a dependence on the fourth-power of the wavelength of the laser used.

See also

* Coherent anti-Stokes Raman spectroscopy (CARS)
* Eckart conditions
* Fermi resonance
* GF method
* Infrared spectroscopy of metal carbonyls
* Lennard-Jones potential
* Near-infrared spectroscopy
* Nuclear resonance vibrational spectroscopy
* Resonance Raman spectroscopy
* Transition dipole moment

References

Further reading

*

External links

Free Molecular Vibration code developed by Zs. Szabó and R. Scipioni





* ttp://symmetry.jacobs-university.de/ Character tables for chemically important point groups
{{Branches of Spectroscopy

Chemical physics
Spectroscopy