Theory of solar cell on:
[Wikipedia]
[Google]
[Amazon]
The theory of solar cells explains the process by which light energy in 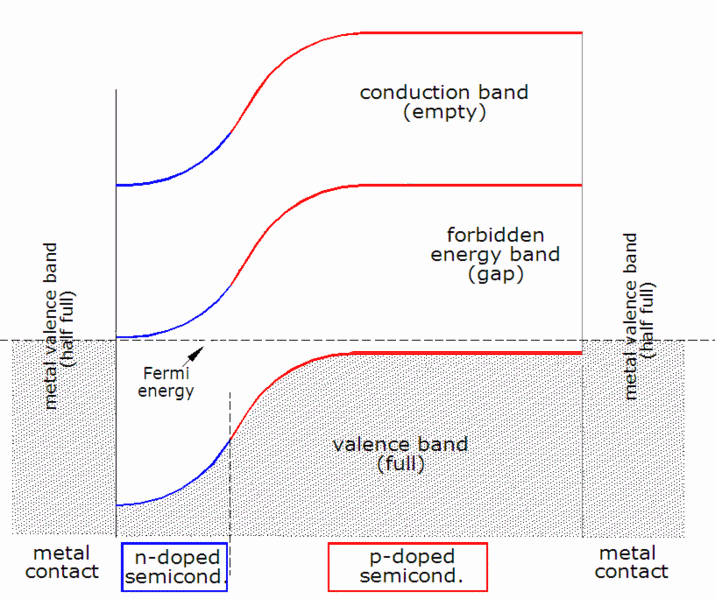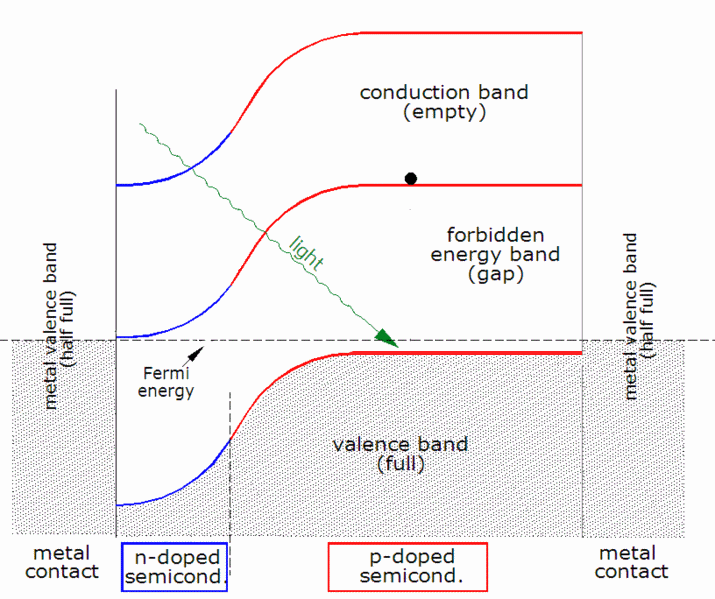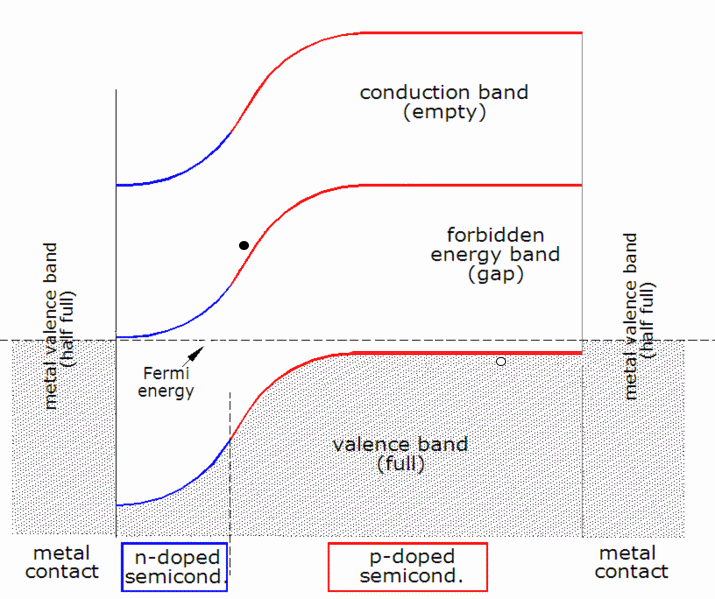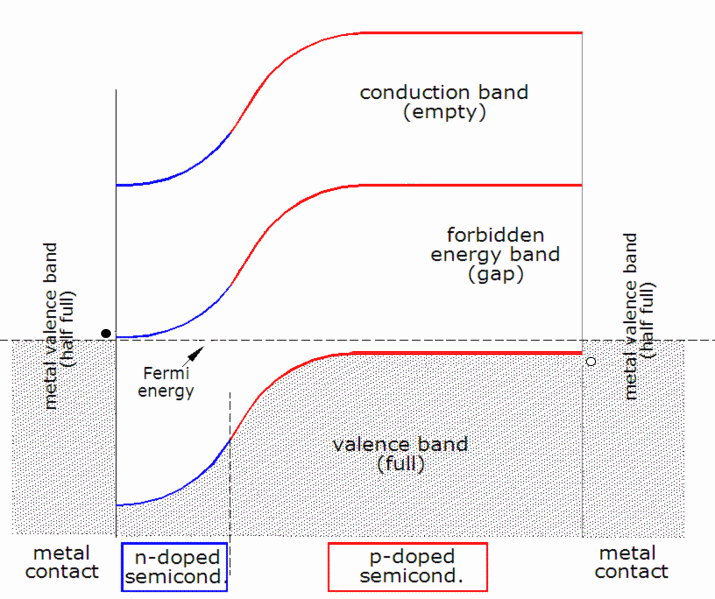
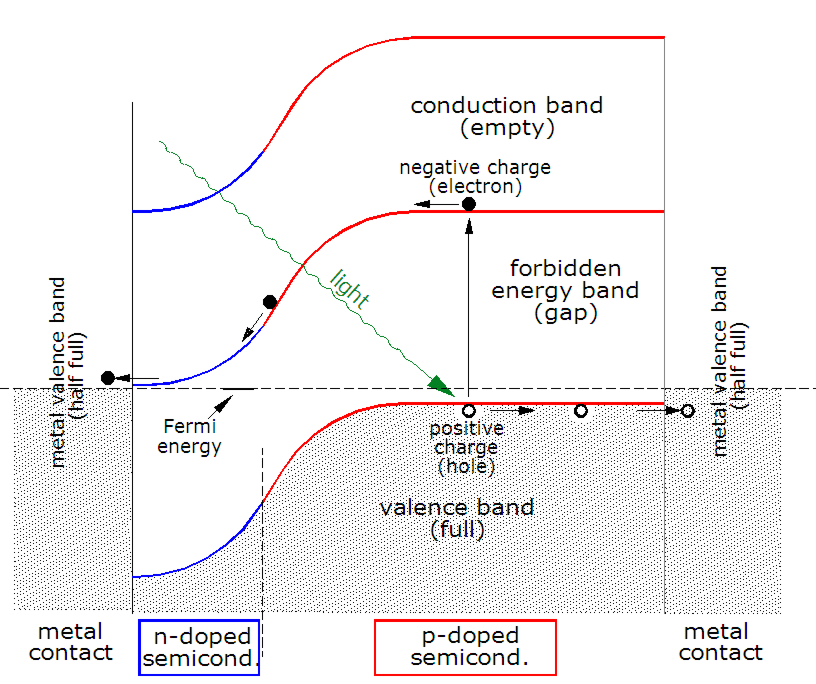 When a photon is absorbed, its energy is given to an electron in the crystal lattice. Usually this electron is in the
When a photon is absorbed, its energy is given to an electron in the crystal lattice. Usually this electron is in the
 An
An
 Transparent conducting electrodes are essential components of solar cells. It is either a continuous film of
Transparent conducting electrodes are essential components of solar cells. It is either a continuous film of
 Temperature affects the characteristic equation in two ways: directly, via ''T'' in the exponential term, and indirectly via its effect on ''I''0 (strictly speaking, temperature affects all of the terms, but these two far more significantly than the others). While increasing ''T'' reduces the magnitude of the exponent in the characteristic equation, the value of ''I''0 increases exponentially with ''T''. The net effect is to reduce ''V''OC (the open-circuit voltage) linearly with increasing temperature. The magnitude of this reduction is inversely proportional to ''V''OC; that is, cells with higher values of ''V''OC suffer smaller reductions in voltage with increasing temperature. For most crystalline silicon solar cells the change in ''V''OC with temperature is about −0.50%/°C, though the rate for the highest-efficiency crystalline silicon cells is around −0.35%/°C. By way of comparison, the rate for amorphous silicon solar cells is −0.20 to −0.30%/°C, depending on how the cell is made.
The amount of photogenerated current ''I''L increases slightly with increasing temperature because of an increase in the number of thermally generated carriers in the cell. This effect is slight, however: about 0.065%/°C for crystalline silicon cells and 0.09% for amorphous silicon cells.
The overall effect of temperature on cell efficiency can be computed using these factors in combination with the characteristic equation. However, since the change in voltage is much stronger than the change in current, the overall effect on efficiency tends to be similar to that on voltage. Most crystalline silicon solar cells decline in efficiency by 0.50%/°C and most amorphous cells decline by 0.15−0.25%/°C. The figure above shows I-V curves that might typically be seen for a crystalline silicon solar cell at various temperatures.
Temperature affects the characteristic equation in two ways: directly, via ''T'' in the exponential term, and indirectly via its effect on ''I''0 (strictly speaking, temperature affects all of the terms, but these two far more significantly than the others). While increasing ''T'' reduces the magnitude of the exponent in the characteristic equation, the value of ''I''0 increases exponentially with ''T''. The net effect is to reduce ''V''OC (the open-circuit voltage) linearly with increasing temperature. The magnitude of this reduction is inversely proportional to ''V''OC; that is, cells with higher values of ''V''OC suffer smaller reductions in voltage with increasing temperature. For most crystalline silicon solar cells the change in ''V''OC with temperature is about −0.50%/°C, though the rate for the highest-efficiency crystalline silicon cells is around −0.35%/°C. By way of comparison, the rate for amorphous silicon solar cells is −0.20 to −0.30%/°C, depending on how the cell is made.
The amount of photogenerated current ''I''L increases slightly with increasing temperature because of an increase in the number of thermally generated carriers in the cell. This effect is slight, however: about 0.065%/°C for crystalline silicon cells and 0.09% for amorphous silicon cells.
The overall effect of temperature on cell efficiency can be computed using these factors in combination with the characteristic equation. However, since the change in voltage is much stronger than the change in current, the overall effect on efficiency tends to be similar to that on voltage. Most crystalline silicon solar cells decline in efficiency by 0.50%/°C and most amorphous cells decline by 0.15−0.25%/°C. The figure above shows I-V curves that might typically be seen for a crystalline silicon solar cell at various temperatures.
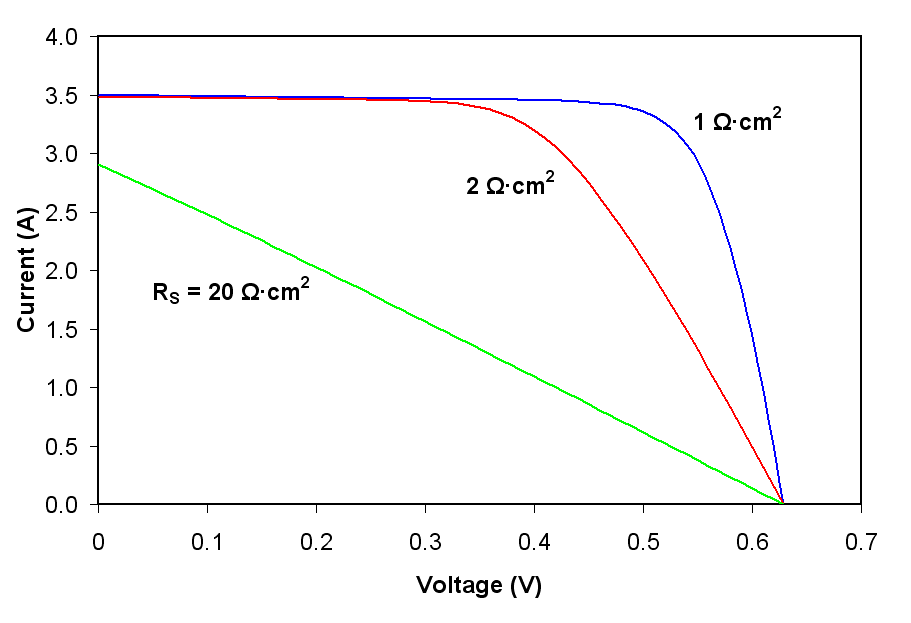 As series resistance increases, the voltage drop between the junction voltage and the terminal voltage becomes greater for the same current. The result is that the current-controlled portion of the I-V curve begins to sag toward the origin, producing a significant decrease in '''' and a slight reduction in ''I''SC, the short-circuit current. Very high values of ''R''S will also produce a significant reduction in ''I''SC; in these regimes, series resistance dominates and the behavior of the solar cell resembles that of a resistor. These effects are shown for crystalline silicon solar cells in the I-V curves displayed in the figure to the right.
Power lost through the series resistance is . During illumination when and are small relative to photocurrent , power loss also increases quadratically with . Series resistance losses are therefore most important at high illumination intensities.
As series resistance increases, the voltage drop between the junction voltage and the terminal voltage becomes greater for the same current. The result is that the current-controlled portion of the I-V curve begins to sag toward the origin, producing a significant decrease in '''' and a slight reduction in ''I''SC, the short-circuit current. Very high values of ''R''S will also produce a significant reduction in ''I''SC; in these regimes, series resistance dominates and the behavior of the solar cell resembles that of a resistor. These effects are shown for crystalline silicon solar cells in the I-V curves displayed in the figure to the right.
Power lost through the series resistance is . During illumination when and are small relative to photocurrent , power loss also increases quadratically with . Series resistance losses are therefore most important at high illumination intensities.
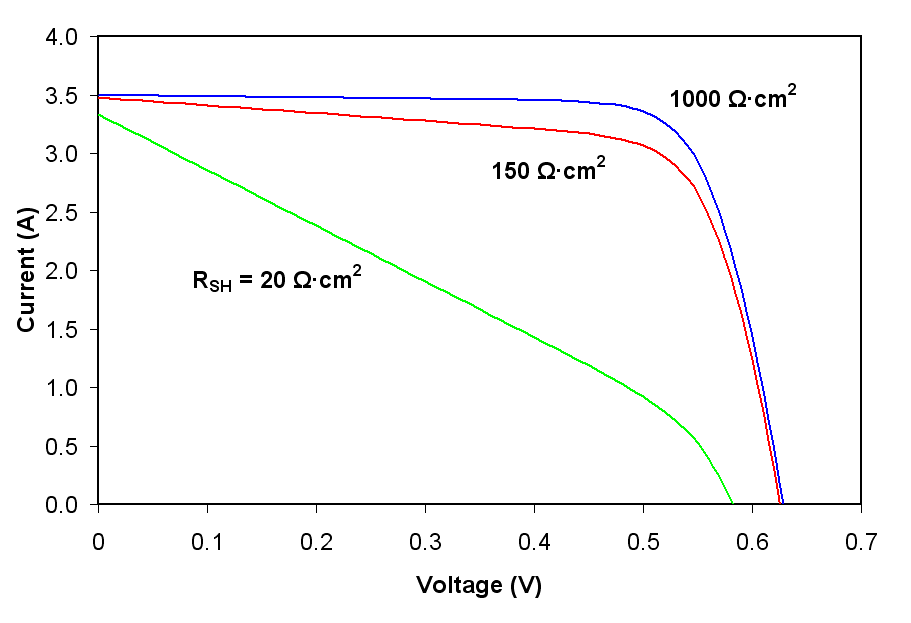 As shunt resistance decreases, the current diverted through the shunt resistor increases for a given level of junction voltage. The result is that the voltage-controlled portion of the I-V curve begins to sag far from the origin, producing a significant decrease in '''' and a slight reduction in ''V''OC. Very low values of ''R''SH will produce a significant reduction in ''V''OC. Much as in the case of a high series resistance, a badly shunted solar cell will take on operating characteristics similar to those of a resistor. These effects are shown for crystalline silicon solar cells in the I-V curves displayed in the figure to the right.
As shunt resistance decreases, the current diverted through the shunt resistor increases for a given level of junction voltage. The result is that the voltage-controlled portion of the I-V curve begins to sag far from the origin, producing a significant decrease in '''' and a slight reduction in ''V''OC. Very low values of ''R''SH will produce a significant reduction in ''V''OC. Much as in the case of a high series resistance, a badly shunted solar cell will take on operating characteristics similar to those of a resistor. These effects are shown for crystalline silicon solar cells in the I-V curves displayed in the figure to the right.
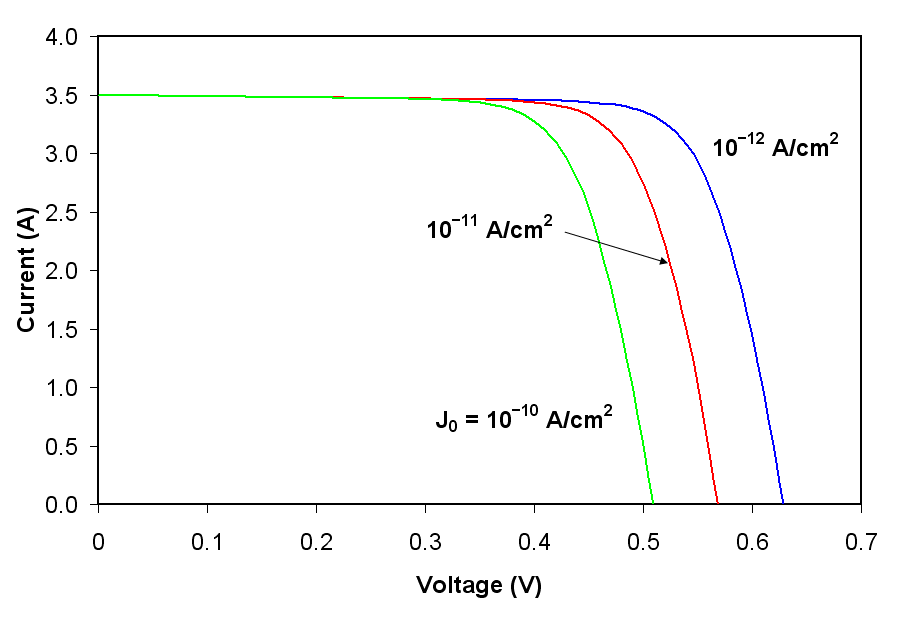 If one assumes infinite shunt resistance, the characteristic equation can be solved for ''V''OC:
:
Thus, an increase in ''I''0 produces a reduction in ''V''OC proportional to the inverse of the logarithm of the increase. This explains mathematically the reason for the reduction in ''V''OC that accompanies increases in temperature described above. The effect of reverse saturation current on the I-V curve of a crystalline silicon solar cell are shown in the figure to the right. Physically, reverse saturation current is a measure of the "leakage" of carriers across the p–n junction in reverse bias. This leakage is a result of carrier recombination in the neutral regions on either side of the junction.
If one assumes infinite shunt resistance, the characteristic equation can be solved for ''V''OC:
:
Thus, an increase in ''I''0 produces a reduction in ''V''OC proportional to the inverse of the logarithm of the increase. This explains mathematically the reason for the reduction in ''V''OC that accompanies increases in temperature described above. The effect of reverse saturation current on the I-V curve of a crystalline silicon solar cell are shown in the figure to the right. Physically, reverse saturation current is a measure of the "leakage" of carriers across the p–n junction in reverse bias. This leakage is a result of carrier recombination in the neutral regions on either side of the junction.
 The ideality factor (also called the emissivity factor) is a fitting parameter that describes how closely the diode's behavior matches that predicted by theory, which assumes the p–n junction of the diode is an infinite plane and no recombination occurs within the space-charge region. A perfect match to theory is indicated when . When recombination in the space-charge region dominate other recombination, however, . The effect of changing ideality factor independently of all other parameters is shown for a crystalline silicon solar cell in the I-V curves displayed in the figure to the right.
Most solar cells, which are quite large compared to conventional diodes, well approximate an infinite plane and will usually exhibit near-ideal behavior under standard test conditions (). Under certain operating conditions, however, device operation may be dominated by recombination in the space-charge region. This is characterized by a significant increase in ''I''0 as well as an increase in ideality factor to . The latter tends to increase solar cell output voltage while the former acts to erode it. The net effect, therefore, is a combination of the increase in voltage shown for increasing ''n'' in the figure to the right and the decrease in voltage shown for increasing ''I''0 in the figure above. Typically, ''I''0 is the more significant factor and the result is a reduction in voltage.
Sometimes, the ideality factor is observed to be greater than 2, which is generally attributed to the presence of Schottky diode or heterojunction in the solar cell. The presence of a heterojunction offset reduces the collection efficiency of the solar cell and may contribute to low fill-factor.
The ideality factor (also called the emissivity factor) is a fitting parameter that describes how closely the diode's behavior matches that predicted by theory, which assumes the p–n junction of the diode is an infinite plane and no recombination occurs within the space-charge region. A perfect match to theory is indicated when . When recombination in the space-charge region dominate other recombination, however, . The effect of changing ideality factor independently of all other parameters is shown for a crystalline silicon solar cell in the I-V curves displayed in the figure to the right.
Most solar cells, which are quite large compared to conventional diodes, well approximate an infinite plane and will usually exhibit near-ideal behavior under standard test conditions (). Under certain operating conditions, however, device operation may be dominated by recombination in the space-charge region. This is characterized by a significant increase in ''I''0 as well as an increase in ideality factor to . The latter tends to increase solar cell output voltage while the former acts to erode it. The net effect, therefore, is a combination of the increase in voltage shown for increasing ''n'' in the figure to the right and the decrease in voltage shown for increasing ''I''0 in the figure above. Typically, ''I''0 is the more significant factor and the result is a reduction in voltage.
Sometimes, the ideality factor is observed to be greater than 2, which is generally attributed to the presence of Schottky diode or heterojunction in the solar cell. The presence of a heterojunction offset reduces the collection efficiency of the solar cell and may contribute to low fill-factor.
PV Lighthouse Equivalent Circuit Calculator
from chemistryexplained.com Theories Solar cells Physical chemistry de:Solarzelle#Funktionsprinzip
photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s is converted into electric current when the photons strike a suitable semiconductor device
A semiconductor device is an electronic component that relies on the electronic properties of a semiconductor material (primarily silicon, germanium, and gallium arsenide, as well as organic semiconductors) for its function. Its conductivit ...
. The theoretical studies are of practical use because they predict the fundamental limits of a solar cell
A solar cell, also known as a photovoltaic cell (PV cell), is an electronic device that converts the energy of light directly into electricity by means of the photovoltaic effect.
, and give guidance on the phenomena that contribute to losses and solar cell efficiency
Solar-cell efficiency is the portion of energy in the form of sunlight that can be converted via photovoltaics into electricity by the solar cell.
The efficiency of the solar cells used in a photovoltaic system, in combination with latitude an ...
.

Working explanation
#Photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s in sunlight
Sunlight is the portion of the electromagnetic radiation which is emitted by the Sun (i.e. solar radiation) and received by the Earth, in particular the visible spectrum, visible light perceptible to the human eye as well as invisible infrare ...
hit the solar panel and are absorbed by semi-conducting materials.
# Electrons
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
(negatively charged) are knocked loose from their atoms as they are excited. Due to their special structure and the materials in solar cells, the electrons are only allowed to move in a single direction. The electronic structure of the materials is very important for the process to work, and often silicon
Silicon is a chemical element; it has symbol Si and atomic number 14. It is a hard, brittle crystalline solid with a blue-grey metallic lustre, and is a tetravalent metalloid (sometimes considered a non-metal) and semiconductor. It is a membe ...
incorporating small amounts of boron
Boron is a chemical element; it has symbol B and atomic number 5. In its crystalline form it is a brittle, dark, lustrous metalloid; in its amorphous form it is a brown powder. As the lightest element of the boron group it has three ...
or phosphorus
Phosphorus is a chemical element; it has Chemical symbol, symbol P and atomic number 15. All elemental forms of phosphorus are highly Reactivity (chemistry), reactive and are therefore never found in nature. They can nevertheless be prepared ar ...
is used in different layers.
# An array of solar cells converts solar energy into a usable amount of direct current
Direct current (DC) is one-directional electric current, flow of electric charge. An electrochemical cell is a prime example of DC power. Direct current may flow through a conductor (material), conductor such as a wire, but can also flow throug ...
(DC) electricity.
Photogeneration of charge carriers
When aphoton
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
hits a piece of semiconductor, one of three things can happen:
# The photon can pass straight through the semiconductor — this (generally) happens for lower energy photons.
# The photon can reflect off the surface.
# The photon can be absorbed by the semiconductor if the photon energy is higher than the band gap
In solid-state physics and solid-state chemistry, a band gap, also called a bandgap or energy gap, is an energy range in a solid where no electronic states exist. In graphs of the electronic band structure of solids, the band gap refers to t ...
value. This generates an electron-hole pair and sometimes heat depending on the band structure.
 When a photon is absorbed, its energy is given to an electron in the crystal lattice. Usually this electron is in the
When a photon is absorbed, its energy is given to an electron in the crystal lattice. Usually this electron is in the valence band
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in ...
. The energy given to the electron by the photon "excites" it into the conduction band
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in ...
where it is free to move around within the semiconductor. The network of covalent bonds that the electron was previously a part of now has one fewer electron. This is known as a hole, and it has positive charge. The presence of a missing covalent bond allows the bonded electrons of neighboring atoms to move into the "hole", leaving another hole behind, thus propagating holes throughout the lattice in the opposite direction to the movement of the negatively electrons. It can be said that photons absorbed in the semiconductor create electron-hole pairs.
A photon only needs to have energy greater than that of the band gap in order to excite an electron from the valence band into the conduction band. However, the solar frequency spectrum
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed int ...
approximates a black body
A black body or blackbody is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. The radiation emitted by a black body in thermal equilibrium with its environment is ...
spectrum at about 5,800 K, and as such, much of the solar radiation reaching the Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
is composed of photons with energies greater than the band gap of silicon (1.12eV), which is near to the ideal value for a terrestrial solar cell (1.4eV). These higher energy photons will be absorbed by a silicon solar cell, but the difference in energy between these photons and the silicon band gap is converted into heat (via lattice vibrations — called phonons
A phonon is a collective excitation in a periodic, Elasticity (physics), elastic arrangement of atoms or molecules in condensed matter physics, condensed matter, specifically in solids and some liquids. In the context of optically trapped objects ...
) rather than into usable electrical energy.
The p–n junction
The most commonly known solar cell is configured as a large-area p–n junction made from silicon. As a simplification, one can imagine bringing a layer of n-type silicon into direct contact with a layer of p-type silicon. n-type doping produces mobile electrons (leaving behind positively charged donors) while p-type doping produces mobile holes (and negatively charged acceptors). In practice, p–n junctions of silicon solar cells are not made in this way, but rather by diffusing an n-type dopant into one side of a p-type wafer (or vice versa). If a piece of p-type silicon is placed in close contact with a piece of n-type silicon, then adiffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical p ...
of electrons occurs from the region of high electron concentration (the n-type side of the junction) into the region of low electron concentration (p-type side of the junction). When the electrons diffuse into the p-type side, each one annihilates a hole, making that side net negatively charged (because now the number of mobile positive holes is now less than the number of negative acceptors). Similarly, holes diffusing to the n-type side make it more positively charged. However (in the absence of an external circuit) this diffusion current
Diffusion current is a current in a semiconductor caused by the diffusion of charge carriers (electrons and/or electron holes). This is the current which is due to the transport of charges occurring because of non-uniform concentration of charge ...
of carriers does not go on indefinitely because the charge build up on either side of the junction produces an electric field
An electric field (sometimes called E-field) is a field (physics), physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) descri ...
that opposes further diffusion of more charges. Eventually, an equilibrium is reached where the net current is zero, leaving a region either side of the junction where electrons and holes have diffused across the junction and annihilated each other called the depletion region
In semiconductor physics, the depletion region, also called depletion layer, depletion zone, junction region, space charge region, or space charge layer, is an insulating region within a conductive, doped semiconductor material where the mobil ...
because it contains practically no mobile charge carriers. It is also known as the ''space charge region'', although space charge extends a bit further in both directions than the depletion region.
Once equilibrium is established, electron-hole pairs generated in the depletion region are separated by the electric field, with the electron attracted to the positive n-type side and holes to the negative p-type side, reducing the charge (and the electric field) built up by the diffusion just described. If the device is unconnected (or the external load is very high) then diffusion current would eventually restore the equilibrium charge by bringing the electron and hole back across the junction, but if the load connected is small enough, the electrons prefer to go around the external circuit in their attempt to restore equilibrium, doing useful work on the way.
Charge carrier separation
There are two causes of charge carrier motion and separation in a solar cell: #drift of carriers, driven by the electric field, with electrons being pushed one way and holes the other way #diffusion of carriers from zones of higher carrier concentration to zones of lower carrier concentration (following a gradient of chemical potential). These two "forces" may work one against the other at any given point in the cell. For instance, an electron moving through the junction from the p region to the n region (as in the diagram at the beginning of this article) is being pushed by the electric field against the concentration gradient. The same goes for a hole moving in the opposite direction. It is easiest to understand how a current is generated when considering electron-hole pairs that are created in the depletion zone, which is where there is a strong electric field. The electron is pushed by this field toward the n side and the hole toward the p side. (This is opposite to the direction of current in a forward-biased diode, such as alight-emitting diode
A light-emitting diode (LED) is a semiconductor device that emits light when current flows through it. Electrons in the semiconductor recombine with electron holes, releasing energy in the form of photons. The color of the light (corre ...
in operation.) When the pair is created outside the space charge zone, where the electric field is smaller, diffusion also acts to move the carriers, but the junction still plays a role by sweeping any electrons that reach it from the p side to the n side, and by sweeping any holes that reach it from the n side to the p side, thereby creating a concentration gradient outside the space charge zone.
In thick solar cells there is very little electric field in the active region outside the space charge zone, so the dominant mode of charge carrier separation is diffusion. In these cells the diffusion length of minority carriers (the length that photo-generated carriers can travel before they recombine) must be large compared to the cell thickness. In thin film cells (such as amorphous silicon), the diffusion length of minority carriers is usually very short due to the existence of defects, and the dominant charge separation is therefore drift, driven by the electrostatic field of the junction, which extends to the whole thickness of the cell.
Once the minority carrier enters the drift region, it is 'swept' across the junction and, at the other side of the junction, becomes a majority carrier. This reverse current is a generation current, fed both thermally and (if present) by the absorption of light. On the other hand, majority carriers are driven into the drift region by diffusion (resulting from the concentration gradient), which leads to the forward current; only the majority carriers with the highest energies (in the so-called Boltzmann tail; cf. Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...
) can fully cross the drift region. Therefore, the carrier distribution in the whole device is governed by a dynamic equilibrium between reverse current and forward current.
Connection to an external load
Ohmicmetal
A metal () is a material that, when polished or fractured, shows a lustrous appearance, and conducts electrical resistivity and conductivity, electricity and thermal conductivity, heat relatively well. These properties are all associated wit ...
-semiconductor contacts are made to both the n-type and p-type sides of the solar cell, and the electrodes
An electrode is an electrical conductor used to make contact with a nonmetallic part of a circuit (e.g. a semiconductor, an electrolyte, a vacuum or a gas). In electrochemical cells, electrodes are essential parts that can consist of a variety ...
connected to an external load. Electrons that are created on the n-type side, or created on the p-type side, "collected" by the junction and swept onto the n-type side, may travel through the wire, power the load, and continue through the wire until they reach the p-type semiconductor-metal contact. Here, they recombine with a hole that was either created as an electron-hole pair on the p-type side of the solar cell, or a hole that was swept across the junction from the n-type side after being created there.
The voltage measured is equal to the difference in the quasi Fermi levels of the majority carriers (electrons in the n-type portion and holes in the p-type portion) at the two terminals.
Equivalent circuit of a solar cell
equivalent circuit
In electrical engineering, an equivalent circuit refers to a theoretical circuit that retains all of the electrical characteristics of a given circuit. Often, an equivalent circuit is sought that simplifies calculation, and more broadly, that is ...
model of an ideal solar cell's p–n junction uses an ideal current source
A current source is an electronic circuit that delivers or absorbs an electric current which is independent of the voltage across it.
A current source is the dual of a voltage source. The term ''current sink'' is sometimes used for sources fed ...
(whose photogenerated current increases with light intensity) in parallel with a diode
A diode is a two-Terminal (electronics), terminal electronic component that conducts electric current primarily in One-way traffic, one direction (asymmetric electrical conductance, conductance). It has low (ideally zero) Electrical resistance ...
(whose current represents recombination losses). To account for resistive losses
Joule heating (also known as resistive heating, resistance heating, or Ohmic heating) is the process by which the passage of an electric current through a conductor produces heat.
Joule's first law (also just Joule's law), also known in countri ...
, a shunt resistance and a series resistance are added as lumped elements. The resulting output current '''' equals the photogenerated current minus the currents through the diode and shunt resistor:
:
The junction voltage (across both the diode and shunt resistance) is:
:
where is the voltage across the output terminals. The leakage current
In electronics, leakage is the gradual transfer of electrical energy across a boundary normally viewed as insulating, such as the spontaneous discharge of a charged capacitor, magnetic coupling of a transformer with other components, or flow ...
through the shunt resistor is proportional to the junction's voltage , according to Ohm's law
Ohm's law states that the electric current through a Electrical conductor, conductor between two Node (circuits), points is directly Proportionality (mathematics), proportional to the voltage across the two points. Introducing the constant of ...
:
:
By the Shockley diode equation
The Shockley diode equation, or the diode law, named after transistor co-inventor William Shockley of Bell Labs, models the exponential current–voltage (I–V) relationship of semiconductor diodes in moderate constant current forward bias or ...
, the current diverted through the diode is:
:
where
*''I''0, reverse saturation current
The saturation current (or scale current), more accurately the reverse saturation current, is the part of the reverse current in a semiconductor diode caused by diffusion of minority carriers from the neutral regions to the depletion region. This ...
*''n'', diode ideality factor
In electronics, diode modelling refers to the mathematical models used to approximate the actual behaviour of real diodes to enable calculations and circuit analysis. A diode's I- V curve is nonlinear.
A very accurate, but complicated, physical ...
(1 for an ideal diode)
*''q'', elementary charge
The elementary charge, usually denoted by , is a fundamental physical constant, defined as the electric charge carried by a single proton (+1 ''e'') or, equivalently, the magnitude of the negative electric charge carried by a single electron, ...
*''k'', Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the ...
*''T'', absolute temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion.
Thermodynamic temperature is typically expres ...
* the thermal voltage
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas ...
. At 25 °C, volt.
Substituting these into the first equation produces the characteristic equation of a solar cell, which relates solar cell parameters to the output current and voltage:
:
An alternative derivation produces an equation similar in appearance, but with on the left-hand side. The two alternatives are identities; that is, they yield precisely the same results.
Since the parameters ''I''0, ''n'', ''R''S, and ''R''SH cannot be measured directly, the most common application of the characteristic equation is nonlinear regression
In statistics, nonlinear regression is a form of regression analysis in which observational data are modeled by a function which is a nonlinear combination of the model parameters and depends on one or more independent variables. The data are fi ...
to extract the values of these parameters on the basis of their combined effect on solar cell behavior.
When ''R''S is not zero, the above equation does not give directly, but it can then be solved using the Lambert W function
In mathematics, the Lambert function, also called the omega function or product logarithm, is a multivalued function, namely the Branch point, branches of the converse relation of the function , where is any complex number and is the expone ...
:
:
When an external load is used with the cell, its resistance can simply be added to ''R''S and '''' set to zero in order to find the current.
When is small, we can use the approximation as to produce something much easier to work with
:
Several further simplifications are now possible, such as when which leads to
:
When the current generated by the PV is large compared with the current in the shunt, i.e. (because the shunt resistance is large) there is an analytical solution for '''' for any less than :
:
Otherwise one can solve for '''' using the Lambert W function:
:
However, when ''R''SH is large it's better to solve the original equation numerically.
The general form of the solution is a curve with '''' decreasing as '''' increases (see graphs lower down). The slope at small or negative '''' (where the ''W'' function is near zero) approaches , whereas the slope at high '''' approaches . Therefore for high optimum output power , it is desirable to have large and should be small.
Open-circuit voltage and short-circuit current
When the cell is operated atopen circuit Open circuit may refer to:
* Open circuit breathing apparatus, any type of breathing apparatus where the exhaled gas is discharged to the surroundings without recycling any of it
** Open-circuit scuba, a type of Scuba-diving equipment where the user ...
, ''''= 0 and the voltage across the output terminals is defined as the ''open-circuit voltage''. Assuming the shunt resistance is high enough to neglect the final term of the characteristic equation, the open-circuit voltage ''V''OC is:
:
Similarly, when the cell is operated at short circuit
A short circuit (sometimes abbreviated to short or s/c) is an electrical circuit that allows a current to travel along an unintended path with no or very low electrical impedance. This results in an excessive current flowing through the circuit ...
, '''' = 0 and the current '''' through the terminals is defined as the ''short-circuit current''. It can be shown that for a high-quality solar cell (low ''R''S and ''I''0, and high ''R''SH) the short-circuit current is:
:
It is not possible to extract any power from the device when operating at either open circuit or short circuit conditions.
Effect of physical size
The values of ''IL'', ''I''0, ''RS'', and ''R''SH are dependent upon the physical size of the solar cell. In comparing otherwise identical cells, a cell with twice the junction area of another will, in principle, have double the ''I''L and ''I''0 because it has twice the area where photocurrent is generated and across which diode current can flow. By the same argument, it will also have half the ''R''S of the series resistance related to vertical current flow; however, for large-area silicon solar cells, the scaling of the series resistance encountered by lateral current flow is not easily predictable since it will depend crucially on the grid design (it is not clear what "otherwise identical" means in this respect). Depending on the shunt type, the larger cell may also have half the ''R''SH because it has twice the area where shunts may occur; on the other hand, if shunts occur mainly at the perimeter, then ''R''SH will decrease according to the change in circumference, not area. Since the changes in the currents are the dominating ones and are balancing each other, the open-circuit voltage is practically the same; ''V''OC starts to depend on the cell size only if ''R''SH becomes too low. To account for the dominance of the currents, the characteristic equation is frequently written in terms ofcurrent density
In electromagnetism, current density is the amount of charge per unit time that flows through a unit area of a chosen cross section. The current density vector is defined as a vector whose magnitude is the electric current per cross-sectional ...
, or current produced per unit cell area:
:
where
*''J'', current density (ampere/cm2)
*''J''L, photogenerated current density (ampere/cm2)
*''J''0, reverse saturation current density (ampere/cm2)
*''r''S, specific series resistance (Ω·cm2)
*''r''SH, specific shunt resistance (Ω·cm2).
This formulation has several advantages. One is that since cell characteristics are referenced to a common cross-sectional area they may be compared for cells of different physical dimensions. While this is of limited benefit in a manufacturing setting, where all cells tend to be the same size, it is useful in research and in comparing cells between manufacturers. Another advantage is that the density equation naturally scales the parameter values to similar orders of magnitude, which can make numerical extraction of them simpler and more accurate even with naive solution methods.
There are practical limitations of this formulation. For instance, certain parasitic effects grow in importance as cell sizes shrink and can affect the extracted parameter values. Recombination and contamination of the junction tend to be greatest at the perimeter of the cell, so very small cells may exhibit higher values of ''J''0 or lower values of ''R''SH than larger cells that are otherwise identical. In such cases, comparisons between cells must be made cautiously and with these effects in mind.
This approach should only be used for comparing solar cells with comparable layout. For instance, a comparison between primarily quadratical solar cells like typical crystalline silicon solar cells and narrow but long solar cells like typical thin film solar cell
Thin-film solar cells are a type of solar cell made by depositing one or more thin layers (thin films or TFs) of photovoltaic material onto a substrate, such as glass, plastic or metal. Thin-film solar cells are typically a few nanometers ( nm ...
s can lead to wrong assumptions caused by the different kinds of current paths and therefore the influence of, for instance, a distributed series resistance contribution to ''r''S. Macro-architecture of the solar cells could result in different surface areas being placed in any fixed volume - particularly for thin film solar cells and flexible solar cells which may allow for highly convoluted folded structures. If volume is the binding constraint, then efficiency density based on surface area may be of less relevance.
Transparent conducting electrodes
 Transparent conducting electrodes are essential components of solar cells. It is either a continuous film of
Transparent conducting electrodes are essential components of solar cells. It is either a continuous film of indium tin oxide
Indium tin oxide (ITO) is a ternary composition of indium, tin and oxygen in varying proportions. Depending on the oxygen content, it can be described as either a ceramic or an alloy. Indium tin oxide is typically encountered as an oxygen-saturate ...
or a conducting wire network, in which wires are charge collectors while voids between wires are transparent for light. An optimum density of wire network is essential for the maximum solar cell performance as higher wire density blocks the light transmittance while lower wire density leads to high recombination losses due to more distance traveled by the charge carriers.
Cell temperature
 Temperature affects the characteristic equation in two ways: directly, via ''T'' in the exponential term, and indirectly via its effect on ''I''0 (strictly speaking, temperature affects all of the terms, but these two far more significantly than the others). While increasing ''T'' reduces the magnitude of the exponent in the characteristic equation, the value of ''I''0 increases exponentially with ''T''. The net effect is to reduce ''V''OC (the open-circuit voltage) linearly with increasing temperature. The magnitude of this reduction is inversely proportional to ''V''OC; that is, cells with higher values of ''V''OC suffer smaller reductions in voltage with increasing temperature. For most crystalline silicon solar cells the change in ''V''OC with temperature is about −0.50%/°C, though the rate for the highest-efficiency crystalline silicon cells is around −0.35%/°C. By way of comparison, the rate for amorphous silicon solar cells is −0.20 to −0.30%/°C, depending on how the cell is made.
The amount of photogenerated current ''I''L increases slightly with increasing temperature because of an increase in the number of thermally generated carriers in the cell. This effect is slight, however: about 0.065%/°C for crystalline silicon cells and 0.09% for amorphous silicon cells.
The overall effect of temperature on cell efficiency can be computed using these factors in combination with the characteristic equation. However, since the change in voltage is much stronger than the change in current, the overall effect on efficiency tends to be similar to that on voltage. Most crystalline silicon solar cells decline in efficiency by 0.50%/°C and most amorphous cells decline by 0.15−0.25%/°C. The figure above shows I-V curves that might typically be seen for a crystalline silicon solar cell at various temperatures.
Temperature affects the characteristic equation in two ways: directly, via ''T'' in the exponential term, and indirectly via its effect on ''I''0 (strictly speaking, temperature affects all of the terms, but these two far more significantly than the others). While increasing ''T'' reduces the magnitude of the exponent in the characteristic equation, the value of ''I''0 increases exponentially with ''T''. The net effect is to reduce ''V''OC (the open-circuit voltage) linearly with increasing temperature. The magnitude of this reduction is inversely proportional to ''V''OC; that is, cells with higher values of ''V''OC suffer smaller reductions in voltage with increasing temperature. For most crystalline silicon solar cells the change in ''V''OC with temperature is about −0.50%/°C, though the rate for the highest-efficiency crystalline silicon cells is around −0.35%/°C. By way of comparison, the rate for amorphous silicon solar cells is −0.20 to −0.30%/°C, depending on how the cell is made.
The amount of photogenerated current ''I''L increases slightly with increasing temperature because of an increase in the number of thermally generated carriers in the cell. This effect is slight, however: about 0.065%/°C for crystalline silicon cells and 0.09% for amorphous silicon cells.
The overall effect of temperature on cell efficiency can be computed using these factors in combination with the characteristic equation. However, since the change in voltage is much stronger than the change in current, the overall effect on efficiency tends to be similar to that on voltage. Most crystalline silicon solar cells decline in efficiency by 0.50%/°C and most amorphous cells decline by 0.15−0.25%/°C. The figure above shows I-V curves that might typically be seen for a crystalline silicon solar cell at various temperatures.
Series resistance
Shunt resistance
Reverse saturation current
Ideality factor
Other models
While the above model is most common, other models have been proposed, like the d1MxP discrete model.See also
*References
{{ReflistExternal links
PV Lighthouse Equivalent Circuit Calculator
from chemistryexplained.com Theories Solar cells Physical chemistry de:Solarzelle#Funktionsprinzip