Transpose Graph on:
[Wikipedia]
[Google]
[Amazon]
 In the mathematical and algorithmic study of
In the mathematical and algorithmic study of
 In the mathematical and algorithmic study of
In the mathematical and algorithmic study of graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
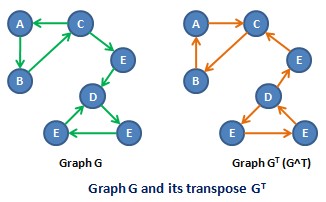
, the converse, transpose or reverse, entry 2.24 of a directed graph is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in . That is, if contains an edge then the converse/transpose/reverse of contains an edge and vice versa.
Notation
The name arises because the reversal of arrows corresponds to taking the converse of an implication in logic. The name is because theadjacency matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph (discrete mathematics), graph. The elements of the matrix (mathematics), matrix indicate whether pairs of Vertex (graph theory), vertices ...
of the transpose directed graph is the transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal;
that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other ...
of the adjacency matrix of the original directed graph.
There is no general agreement on preferred terminology.
The converse is denoted symbolically as , , , or other notations, depending on which terminology is used and which book or article is the source for the notation.
Applications
Although there is little difference mathematically between a graph and its transpose, the difference may be larger incomputer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, depending on how a given graph is represented. For instance, for the web graph, it is easy to determine the outgoing links of a vertex, but hard to determine the incoming links, while in the reversal of this graph the opposite is true. In graph algorithm
An algorithm is fundamentally a set of rules or defined procedures that is typically designed and used to solve a specific problem or a broad set of problems.
Broadly, algorithms define process(es), sets of rules, or methodologies that are to be f ...
s, therefore, it may sometimes be useful to construct an explicit representation of the reversal of a graph, in order to put the graph into a form which is more suitable for the operations being performed on it. An example of this is Kosaraju's algorithm
In computer science, Kosaraju-Sharir's algorithm (also known as Kosaraju's algorithm) is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha S ...
for strongly connected component
In the mathematics, mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachability, reachable from every other vertex. The strongly connected components of a directed graph form a partition of a s ...
s, which applies depth-first search
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible al ...
twice, once to the given graph and a second time to its reversal.
Related concepts
Askew-symmetric graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is graph isomorphism, isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution (math ...
is a graph that is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
to its own transpose graph, via a special kind of isomorphism that pairs up all of the vertices.
The converse relation
In mathematics, the converse of a binary relation is the relation that occurs when the order of the elements is switched in the relation. For example, the converse of the relation 'child of' is the relation 'parent of'. In formal terms ...
of a binary relation
In mathematics, a binary relation associates some elements of one Set (mathematics), set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs ...
is the relation that reverses the ordering of each pair of related objects. If the relation is interpreted as a directed graph, this is the same thing as the transpose of the graph. In particular, the dual order of a partial order
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable ...
can be interpreted in this way as the transposition of a transitively-closed directed acyclic graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one ...
.
See also
*References
{{reflist Graph operations Directed graphs