Transcritical Bifurcation on:
[Wikipedia]
[Google]
[Amazon]
In 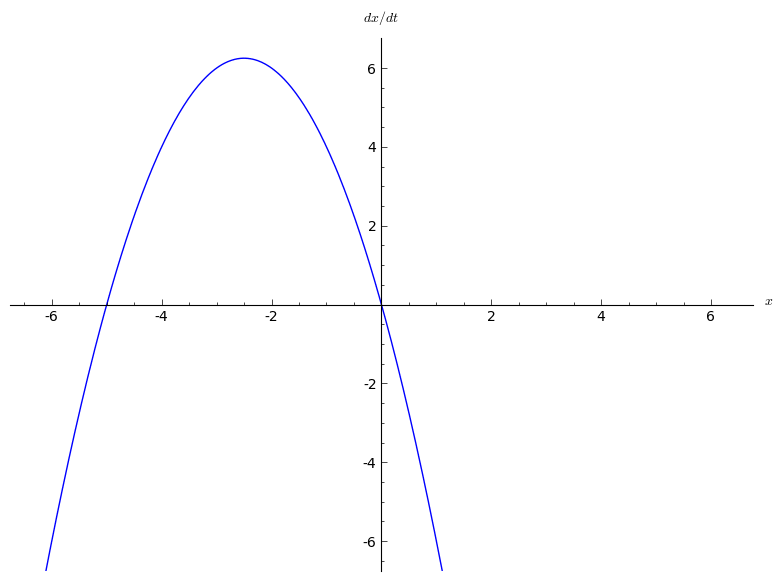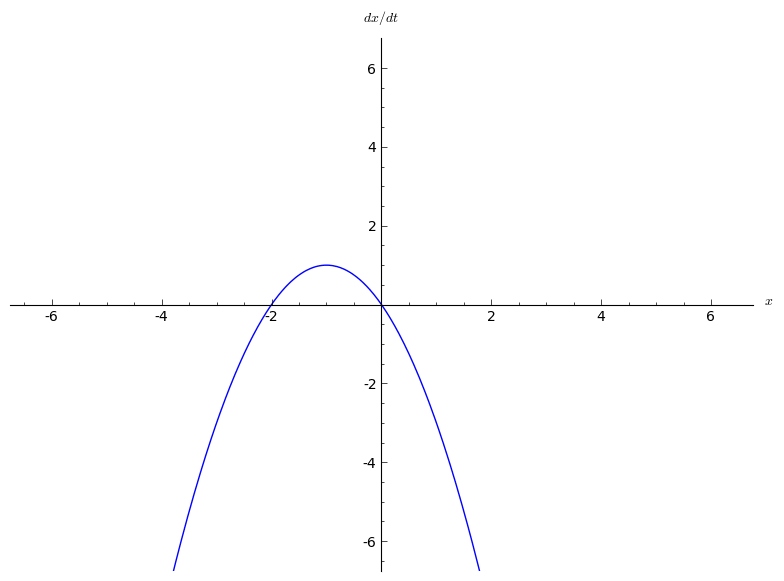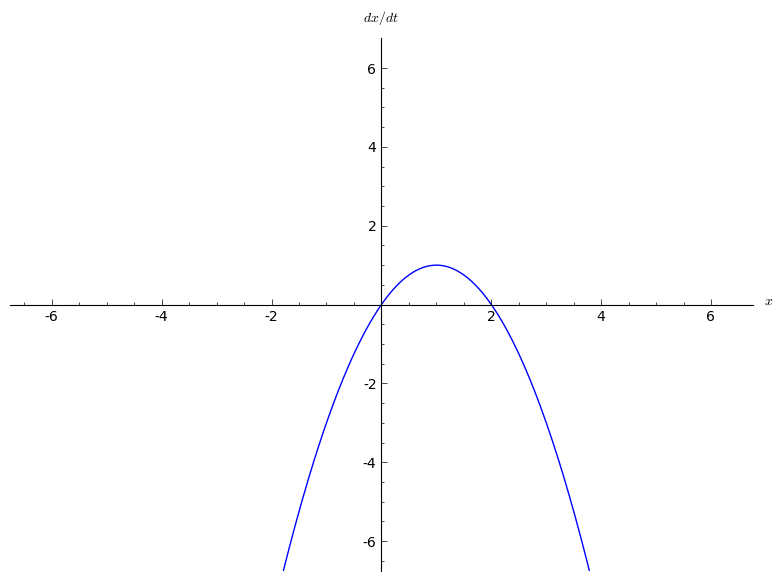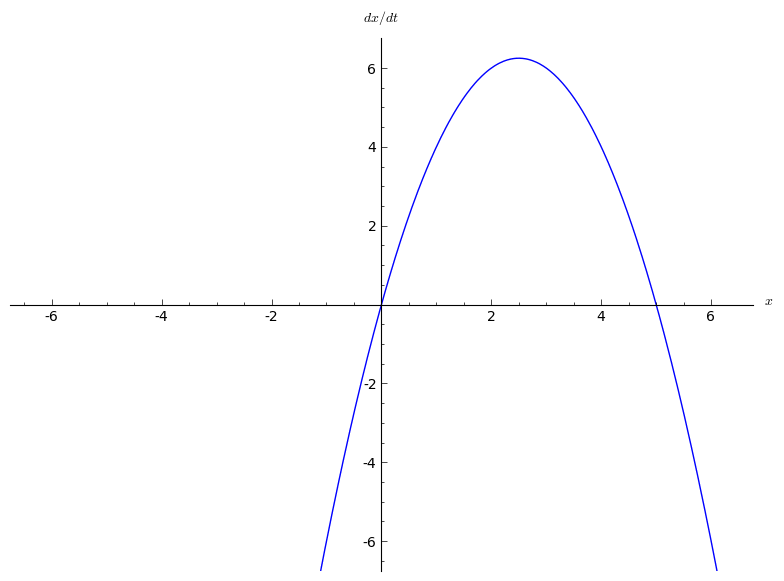 A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa.
The normal form of a transcritical bifurcation is
:
This equation is similar to the logistic equation, but in this case we allow and to be positive or negative (while in the logistic equation and must be non-negative).
The two fixed points are at and . When the parameter is negative, the fixed point at is stable and the fixed point is unstable. But for , the point at is unstable and the point at is stable. So the bifurcation occurs at .
A typical example (in real life) could be the consumer-producer problem where the consumption is proportional to the (quantity of) resource.
For example:
:
where
* is the logistic equation of resource growth; and
* is the consumption, proportional to the resource .
A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa.
The normal form of a transcritical bifurcation is
:
This equation is similar to the logistic equation, but in this case we allow and to be positive or negative (while in the logistic equation and must be non-negative).
The two fixed points are at and . When the parameter is negative, the fixed point at is stable and the fixed point is unstable. But for , the point at is unstable and the point at is stable. So the bifurcation occurs at .
A typical example (in real life) could be the consumer-producer problem where the consumption is proportional to the (quantity of) resource.
For example:
:
where
* is the logistic equation of resource growth; and
* is the consumption, proportional to the resource .
bifurcation theory
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential e ...
, a field within mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
whose real part passes through zero.
 A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa.
The normal form of a transcritical bifurcation is
:
This equation is similar to the logistic equation, but in this case we allow and to be positive or negative (while in the logistic equation and must be non-negative).
The two fixed points are at and . When the parameter is negative, the fixed point at is stable and the fixed point is unstable. But for , the point at is unstable and the point at is stable. So the bifurcation occurs at .
A typical example (in real life) could be the consumer-producer problem where the consumption is proportional to the (quantity of) resource.
For example:
:
where
* is the logistic equation of resource growth; and
* is the consumption, proportional to the resource .
A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa.
The normal form of a transcritical bifurcation is
:
This equation is similar to the logistic equation, but in this case we allow and to be positive or negative (while in the logistic equation and must be non-negative).
The two fixed points are at and . When the parameter is negative, the fixed point at is stable and the fixed point is unstable. But for , the point at is unstable and the point at is stable. So the bifurcation occurs at .
A typical example (in real life) could be the consumer-producer problem where the consumption is proportional to the (quantity of) resource.
For example:
:
where
* is the logistic equation of resource growth; and
* is the consumption, proportional to the resource .
References
{{DEFAULTSORT:Transcritical Bifurcation Bifurcation theory