time-scale calculus on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, time-scale calculus is a unification of the theory of
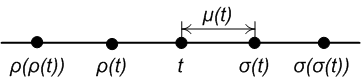 The ''forward jump'' and ''backward jump'' operators represent the closest point in the time scale on the right and left of a given point , respectively. Formally:
: (forward shift/jump operator)
: (backward shift/jump operator)
The ''graininess'' is the distance from a point to the closest point on the right and is given by:
:
For a right-dense , and .
The ''forward jump'' and ''backward jump'' operators represent the closest point in the time scale on the right and left of a given point , respectively. Formally:
: (forward shift/jump operator)
: (backward shift/jump operator)
The ''graininess'' is the distance from a point to the closest point on the right and is given by:
:
For a right-dense , and .
For a left-dense ,
 For any , is:
* ''left dense'' if
* ''right dense'' if
* ''left scattered'' if
* ''right scattered'' if
* ''dense'' if both left dense and right dense
* ''isolated'' if both left scattered and right scattered
As illustrated by the figure at right:
* Point is ''dense''
* Point is ''left dense'' and ''right scattered''
* Point is ''isolated''
* Point is ''left scattered'' and ''right dense''
For any , is:
* ''left dense'' if
* ''right dense'' if
* ''left scattered'' if
* ''right scattered'' if
* ''dense'' if both left dense and right dense
* ''isolated'' if both left scattered and right scattered
As illustrated by the figure at right:
* Point is ''dense''
* Point is ''left dense'' and ''right scattered''
* Point is ''isolated''
* Point is ''left scattered'' and ''right dense''
Dynamic Equations on Time Scales
Special issue of ''Journal of Computational and Applied Mathematics'' (2002)
Special Issue of ''Advances in Difference Equations'' (2006)
Special issue of ''Nonlinear Dynamics And Systems Theory'' (2009)
The Baylor University Time Scales Group
Timescalewiki.org
{{DEFAULTSORT:Time Scale Calculus Dynamical systems Calculus Recurrence relations
difference equation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a paramete ...
s with that of differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...
s, unifying integral and differential calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
with the calculus of finite differences, offering a formalism for studying hybrid system A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both ''flow'' (described by a differential equation) and ''jump'' (described by a state machine or automaton). Often, the ...
s. It has applications in any field that requires simultaneous modelling of discrete and continuous data. It gives a new definition of a derivative such that if one differentiates a function defined on the real numbers then the definition is equivalent to standard differentiation, but if one uses a function defined on the integers then it is equivalent to the forward difference
A finite difference is a mathematical expression of the form . If a finite difference is divided by , one gets a difference quotient. The approximation of derivatives by finite differences plays a central role in finite difference methods for the ...
operator.
History
Time-scale calculus was introduced in 1988 by the German mathematician Stefan Hilger. However, similar ideas have been used before and go back at least to the introduction of theRiemann–Stieltjes integral
In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes. The definition of this integral was first published in 1894 by Stieltjes. It serves as an i ...
, which unifies sums and integrals.
Dynamic equations
Many results concerning differential equations carry over quite easily to corresponding results for difference equations, while other results seem to be completely different from theircontinuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous g ...
counterparts. The study of dynamic equations on time scales reveals such discrepancies, and helps avoid proving results twice—once for differential equations and once again for difference equations. The general idea is to prove a result for a dynamic equation where the domain of the unknown function is a so-called time scale (also known as a time-set), which may be an arbitrary closed subset of the reals. In this way, results apply not only to the set of real number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small var ...
s or set of integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s but to more general time scales such as a Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
T ...
.
The three most popular examples of calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
on time scales are differential calculus, difference calculus, and quantum calculus. Dynamic equations on a time scale have a potential for applications such as in population dynamics
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems.
History
Population dynamics has traditionally been the dominant branch of mathematical biology, which has ...
. For example, they can model insect populations that evolve continuously while in season, die out in winter while their eggs are incubating or dormant, and then hatch in a new season, giving rise to a non-overlapping population.
Formal definitions
A time scale (or measure chain) is aclosed subset
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a c ...
of the real line
In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a po ...
. The common notation for a general time scale is .
The two most commonly encountered examples of time scales are the real numbers and the discrete time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled.
Discrete time
Discrete time views values of variables as occurring at distinct, separate "po ...
scale .
A single point in a time scale is defined as:
:
Operations on time scales
 The ''forward jump'' and ''backward jump'' operators represent the closest point in the time scale on the right and left of a given point , respectively. Formally:
: (forward shift/jump operator)
: (backward shift/jump operator)
The ''graininess'' is the distance from a point to the closest point on the right and is given by:
:
For a right-dense , and .
The ''forward jump'' and ''backward jump'' operators represent the closest point in the time scale on the right and left of a given point , respectively. Formally:
: (forward shift/jump operator)
: (backward shift/jump operator)
The ''graininess'' is the distance from a point to the closest point on the right and is given by:
:
For a right-dense , and .For a left-dense ,
Classification of points
 For any , is:
* ''left dense'' if
* ''right dense'' if
* ''left scattered'' if
* ''right scattered'' if
* ''dense'' if both left dense and right dense
* ''isolated'' if both left scattered and right scattered
As illustrated by the figure at right:
* Point is ''dense''
* Point is ''left dense'' and ''right scattered''
* Point is ''isolated''
* Point is ''left scattered'' and ''right dense''
For any , is:
* ''left dense'' if
* ''right dense'' if
* ''left scattered'' if
* ''right scattered'' if
* ''dense'' if both left dense and right dense
* ''isolated'' if both left scattered and right scattered
As illustrated by the figure at right:
* Point is ''dense''
* Point is ''left dense'' and ''right scattered''
* Point is ''isolated''
* Point is ''left scattered'' and ''right dense''
Continuity
Continuity of a time scale is redefined as equivalent to density. A time scale is said to be ''right-continuous at point '' if it is right dense at point . Similarly, a time scale is said to be ''left-continuous at point '' if it is left dense at point .Derivative
Take a function: : (where R could be anyBanach space
In mathematics, more specifically in functional analysis, a Banach space (pronounced ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between ve ...
, but is set to the real line for simplicity).
Definition: The ''delta derivative'' (also Hilger derivative) exists if and only if:
For every there exists a neighborhood of such that:
:
for all in .
Take Then , , ; is the derivative used in standard calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
. If (the integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s), , , is the forward difference operator
A finite difference is a mathematical expression of the form . If a finite difference is divided by , one gets a difference quotient. The approximation of derivatives by finite differences plays a central role in finite difference methods for t ...
used in difference equations.
Integration
The ''delta integral'' is defined as the antiderivative with respect to the delta derivative. If has a continuous derivative one sets :Laplace transform and z-transform
ALaplace transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform that converts a function of a real variable (usually t, in the ''time domain'') to a function of a complex variable s (in the ...
can be defined for functions on time scales, which uses the same table of transforms for any arbitrary time scale. This transform can be used to solve dynamic equations on time scales. If the time scale is the non-negative integers then the transform is equal to a modified Z-transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain (z-domain or z-plane) representation.
It can be considered as a discrete-t ...
:
Partial differentiation
Partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to ...
s and partial difference equations are unified as partial dynamic equations on time scales.
Multiple integration
Multiple integration on time scales is treated in Bohner (2005).Stochastic dynamic equations on time scales
Stochastic differential equation
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs are used to model various phenomena such as stock ...
s and stochastic difference equations can be generalized to stochastic dynamic equations on time scales.
Measure theory on time scales
Associated with every time scale is a natural measure defined via : where denotesLebesgue measure
In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of ''n''-dimensional Euclidean space. For ''n'' = 1, 2, or 3, it coincides ...
and is the backward shift operator defined on . The delta integral turns out to be the usual Lebesgue–Stieltjes integral with respect to this measure
:
and the delta derivative turns out to be the Radon–Nikodym derivative with respect to this measure
:
Distributions on time scales
TheDirac delta
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire ...
and Kronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 ...
are unified on time scales as the ''Hilger delta'':
:
Integral equations on time scales
Integral equation
In mathematics, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3,...,x_n ; u(x_1,x_2,x_3,...,x_n ...
s and summation equations are unified as integral equations on time scales.
Fractional calculus on time scales
Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D
:D f(x) = \frac f(x)\,,
and of the integration o ...
on time scales is treated in Bastos, Mozyrska, and Torres.
See also
* Analysis on fractals for dynamic equations on aCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
T ...
.
* Multiple-scale analysis
* Method of averaging
* Krylov–Bogoliubov averaging method
References
Further reading
*Dynamic Equations on Time Scales
Special issue of ''Journal of Computational and Applied Mathematics'' (2002)
Special Issue of ''Advances in Difference Equations'' (2006)
Special issue of ''Nonlinear Dynamics And Systems Theory'' (2009)
External links
The Baylor University Time Scales Group
Timescalewiki.org
{{DEFAULTSORT:Time Scale Calculus Dynamical systems Calculus Recurrence relations