Stokes' Theorem on:
[Wikipedia]
[Google]
[Amazon]
Stokes's theorem, also known as the Kelvin–Stokes theorem Nagayoshi Iwahori, et al.:"Bi-Bun-Seki-Bun-Gaku" Sho-Ka-Bou(jp) 1983/12
Written in Japanese)Atsuo Fujimoto;"Vector-Kai-Seki Gendai su-gaku rekucha zu. C(1)" :ja:培風館, Bai-Fu-Kan(jp)(1979/01) [] (Written in Japanese) after Lord Kelvin and Sir George Stokes, 1st Baronet, George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the
/ref> Here, the "" represents
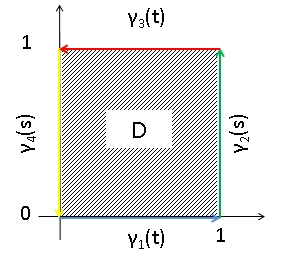 In what follows, we abuse notation and use "" for concatenation of paths in the
In what follows, we abuse notation and use "" for concatenation of paths in the
. See theorems 7 & 8. In other words, the possibility of finding a continuous homotopy, but not being able to integrate over it, is actually eliminated with the benefit of higher mathematics. We thus obtain the following theorem. Theorem 2-2. Let be
Written in Japanese)Atsuo Fujimoto;"Vector-Kai-Seki Gendai su-gaku rekucha zu. C(1)" :ja:培風館, Bai-Fu-Kan(jp)(1979/01) [] (Written in Japanese) after Lord Kelvin and Sir George Stokes, 1st Baronet, George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the
integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
of the curl of the vector field over some surface, to the line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms ''path integral'', ''curve integral'', and ''curvilinear integral'' are also used; '' contour integral'' is used as well, ...
of the vector field around the boundary of the surface. The classical Stokes' theorem can be stated in one sentence: The line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms ''path integral'', ''curve integral'', and ''curvilinear integral'' are also used; '' contour integral'' is used as well, ...
of a vector field over a loop is equal to the '' flux of its curl'' through the enclosed surface.
Stokes' theorem is a special case of the generalized Stokes' theorem. In particular, a vector field on can be considered as a 1-form
In differential geometry, a one-form on a differentiable manifold is a smooth section of the cotangent bundle. Equivalently, a one-form on a manifold M is a smooth mapping of the total space of the tangent bundle of M to \R whose restriction to ...
in which case its curl is its exterior derivative
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899. The re ...
, a 2-form.
Theorem
Let be a smooth oriented surface in with boundary . If a vector field is defined and has continuous first order partial derivatives in a region containing , then More explicitly, the equality says that The main challenge in a precise statement of Stokes' theorem is in defining the notion of a boundary. Surfaces such as the Koch snowflake, for example, are well-known not to exhibit a Riemann-integrable boundary, and the notion of surface measure in Lebesgue theory cannot be defined for a non-Lipschitz Lipschitz, Lipshitz, or Lipchitz, is an Ashkenazi Jewish (Yiddish/German-Jewish) surname. The surname has many variants, including: Lifshitz ( Lifschitz), Lifshits, Lifshuts, Lefschetz; Lipschitz, Lipshitz, Lipshits, Lopshits, Lipschutz (Lip ...
surface. One (advanced) technique is to pass to a weak formulation and then apply the machinery of geometric measure theory; for that approach see the coarea formula. In this article, we instead use a more elementary definition, based on the fact that a boundary can be discerned for full-dimensional subsets of .
A more detailed statement will be given for subsequent discussions;
Let be a piecewise
In mathematics, a piecewise-defined function (also called a piecewise function, a hybrid function, or definition by cases) is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. P ...
smooth Jordan plane curve. The Jordan curve theorem implies that divides into two components, a compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact
* Blood compact, an ancient ritual of the Philippines
* Compact government, a type of colonial rule utilized in Britis ...
one and another that is non-compact. Let denote the compact part; then is bounded by . It now suffices to transfer this notion of boundary along a continuous map to our surface in . But we already have such a map: the parametrization of .
Suppose is piecewise
In mathematics, a piecewise-defined function (also called a piecewise function, a hybrid function, or definition by cases) is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. P ...
smooth at the neighborhood of D, with . represents the image set of ''D'' by ''ψ'' If is the space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
defined by may not be a Jordan curve if the loop interacts poorly with . Nonetheless, is always a loop
Loop or LOOP may refer to:
Brands and enterprises
* Loop (mobile), a Bulgarian virtual network operator and co-founder of Loop Live
* Loop, clothing, a company founded by Carlos Vasquez in the 1990s and worn by Digable Planets
* Loop Mobile, an ...
, and topologically a connected sum of countably many
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbe ...
Jordan curves, so that the integrals are well-defined. then we call the boundary of , written .
With the above notation, if is any smooth vector field on , thenRobert Scheichl, lecture notes for University of Bath mathematics course/ref> Here, the "" represents
Dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alg ...
in .
Proof
The proof of the theorem consists of 4 steps. We assumeGreen's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by . It is the two-dimensional special case of Stokes' theorem.
Theorem
Let be a positively orie ...
, so what is of concern is how to boil down the three-dimensional complicated problem (Stokes' theorem) to a two-dimensional rudimentary problem (Green's theorem). When proving this theorem, mathematicians normally deduce it as a special case of a more general result, which is stated in terms of differential form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many application ...
s, and proved using more sophisticated machinery. While powerful, these techniques require substantial background, so the proof below avoids them, and does not presuppose any knowledge beyond a familiarity with basic vector calculus and linear algebra. At the end of this section, a short alternate proof of Stokes' theorem is given, as a corollary of the generalized Stokes' Theorem.
Elementary proof
First step of the elementary proof (parametrization of integral)
As in , we reduce the dimension by using the natural parametrization of the surface. Let and be as in that section, and note that by change of variables where stands for the Jacobian matrix of at . Now let be an orthonormal basis in the coordinate directions of .In this article, Note that, in some textbooks on vector analysis, these are assigned to different things. For example, in some text book's notation, can mean the following respectively. In this article, however, these are two completely different things. Here, and the "" represents Euclidean norm. Recognizing that the columns of are precisely the partial derivatives of at , we can expand the previous equation in coordinates asSecond step in the elementary proof (defining the pullback)
The previous step suggests we define the function Now, if the scalar value functions and are defined as follows, then, This is thepullback
In mathematics, a pullback is either of two different, but related processes: precomposition and fiber-product. Its dual is a pushforward.
Precomposition
Precomposition with a function probably provides the most elementary notion of pullback: ...
of along , and, by the above, it satisfies
We have successfully reduced one side of Stokes' theorem to a 2-dimensional formula; we now turn to the other side.
Third step of the elementary proof (second equation)
First, calculate the partial derivatives appearing inGreen's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by . It is the two-dimensional special case of Stokes' theorem.
Theorem
Let be a positively orie ...
, via the product rule:
Conveniently, the second term vanishes in the difference, by equality of mixed partials
In mathematics, the symmetry of second derivatives (also called the equality of mixed partials) refers to the possibility of interchanging the order of taking partial derivatives of a function
:f\left(x_1,\, x_2,\, \ldots,\, x_n\right)
of ''n ...
. So,
For all , for all Square matrix, and therefore .
But now consider the matrix in that quadratic form—that is, . We claim this matrix in fact describes a cross product.
Here the "" represents the Matrix transpose operator.
To be precise, let be an arbitrary matrix and let
Note that is linear, so it is determined by its action on basis elements. But by direct calculation
Here, represents an orthonormal basis in the coordinate directions of .In this article,
Note that, in some textbooks on vector analysys, these are assigned to different things.
Thus for any .
Substituting for , we obtain
We can now recognize the difference of partials as a (scalar) triple product:
On the other hand, the definition of a surface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one ...
also includes a triple product—the very same one!
So, we obtain
Fourth step of the elementary proof (reduction to Green's theorem)
Combining the second and third steps, and then applyingGreen's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by . It is the two-dimensional special case of Stokes' theorem.
Theorem
Let be a positively orie ...
completes the proof.
Green's theorem asserts the following: for any region D bounded by the Jordans closed curve γ and two scalar-valued smooth functions defined on D;
We can substitute the conclusion of STEP2 into the left-hand side of Green's theorem above, and substitute the conclusion of STEP3 into the right-hand side.
Q.E.D.
Q.E.D. or QED is an initialism of the Latin phrase , meaning "which was to be demonstrated". Literally it states "what was to be shown". Traditionally, the abbreviation is placed at the end of mathematical proofs and philosophical arguments in pri ...
Proof via differential forms
The functions can be identified with the differential 1-forms on via the map Write the differential 1-form associated to a function as . Then one can calculate that where is theHodge star
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of ...
and is the exterior derivative
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899. The re ...
. Thus, by generalized Stokes' theorem,
Applications
Irrotational fields
In this section, we will discuss the irrotational field ( lamellar vector field) based on Stokes' theorem. Definition 2-1 (irrotational field). A smooth vector field on anopen
Open or OPEN may refer to:
Music
* Open (band), Australian pop/rock band
* The Open (band), English indie rock band
* Open (Blues Image album), ''Open'' (Blues Image album), 1969
* Open (Gotthard album), ''Open'' (Gotthard album), 1999
* Open (C ...
is ''irrotational''( lamellar vector field) if .
This concept is very fundamental in mechanics; as we'll prove later, if is ''irrotational'' and the domain of is simply connected, then is a conservative vector field.
The Helmholtz's theorems
In this section, we will introduce a theorem that is derived from Stokes' theorem and characterizes vortex-free vector fields. In fluid dynamics it is called Helmholtz's theorems. Theorem 2-1 (Helmholtz's theorem in fluid dynamics). Let be anopen
Open or OPEN may refer to:
Music
* Open (band), Australian pop/rock band
* The Open (band), English indie rock band
* Open (Blues Image album), ''Open'' (Blues Image album), 1969
* Open (Gotthard album), ''Open'' (Gotthard album), 1999
* Open (C ...
subset
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ...
with a lamellar vector field and let be piecewise smooth loops. If there is a function such that
* LH0'' is piecewise smooth,
* LH1'' for all ,
* LH2'' for all ,
* LH3'' for all .
Then,
Some textbooks such as Lawrence call the relationship between and stated in theorem 2-1 as "homotopic" and the function as "homotopy between and ". However, "homotopic" or "homotopy" in above-mentioned sense are different (stronger than) typical definitions of "homotopic" or "homotopy"; the latter omit condition LH3 So from now on we refer to homotopy (homotope) in the sense of theorem 2-1 as a ''tubular homotopy (resp. tubular-homotopic)''.
=Proof of the Helmholtz's theorems
= In what follows, we abuse notation and use "" for concatenation of paths in the
In what follows, we abuse notation and use "" for concatenation of paths in the fundamental groupoid In algebraic topology, the fundamental groupoid is a certain topological invariant of a topological space. It can be viewed as an extension of the more widely-known fundamental group; as such, it captures information about the homotopy type of a ...
and "" for reversing the orientation of a path.
Let , and split into four line segments .
so that
By our assumption that and are piecewise smooth homotopic, there is a piecewise smooth homotopy
Let be the image of under . That
follows immediately from Stokes' theorem. is lamellar, so the left side vanishes, i.e.
As is tubular(satisfying LH3, and . Thus the line integrals along and cancel, leaving
On the other hand, , , so that the desired equality follows almost immediately.
Conservative forces
Above Helmholtz's theorem gives an explanation as to why the work done by a conservative force in changing an object's position is path independent. First, we introduce the Lemma 2-2, which is a corollary of and a special case of Helmholtz's theorem. Lemma 2-2. Let be anopen
Open or OPEN may refer to:
Music
* Open (band), Australian pop/rock band
* The Open (band), English indie rock band
* Open (Blues Image album), ''Open'' (Blues Image album), 1969
* Open (Gotthard album), ''Open'' (Gotthard album), 1999
* Open (C ...
subset
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ...
, with a Lamellar vector field and a piecewise smooth loop . Fix a point , if there is a homotopy such that
* C0'' is ''piecewise smooth'',
* C1'' for all ,
* C2'' for all ,
* C3'' for all .
Then,
Above Lemma 2-2 follows from theorem 2–1. In Lemma 2-2, the existence of satisfying C0to C3is crucial;the question is whether such a homotopy can be taken for arbitrary loops. If is simply connected, such exists. The definition of simply connected space follows:
Definition 2-2 (simply connected space). Let be non-empty and path-connected. is called simply connected if and only if for any continuous loop, there exists a continuous tubular homotopy from to a fixed point ; that is,
* C0'
C, or c, is the third letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''cee'' (pronounced ), plural ''cees''.
History
"C" ...
'' is ''continuous'',
* C1'' for all ,
* C2'' for all ,
* C3'' for all .
The claim that "for a conservative force, the work done in changing an object's position is path independent" might seem to follow immediately if the M is simply connected. However, recall that simple-connection only guarantees the existence of a ''continuous'' homotopy satisfying C1-3 we seek a piecewise smooth homotopy satisfying those conditions instead.
Fortunately, the gap in regularity is resolved by the Whitney's approximation theorem.L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, American Mathematical Society Translations, Ser. 2, Vol. 11, American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meeting ...
, Providence, R.I., 1959, pp. 1–114. (22 #598. See theorems 7 & 8. In other words, the possibility of finding a continuous homotopy, but not being able to integrate over it, is actually eliminated with the benefit of higher mathematics. We thus obtain the following theorem. Theorem 2-2. Let be
open
Open or OPEN may refer to:
Music
* Open (band), Australian pop/rock band
* The Open (band), English indie rock band
* Open (Blues Image album), ''Open'' (Blues Image album), 1969
* Open (Gotthard album), ''Open'' (Gotthard album), 1999
* Open (C ...
and simply connected with an irrotational vector field . For all piecewise smooth loops
Maxwell's equations
In the physics ofelectromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
, Stokes' theorem provides the justification for the equivalence of the differential form of the Maxwell–Faraday equation and the Maxwell–Ampère equation and the integral form of these equations. For Faraday's law, Stokes' theorem is applied to the electric field, :
For Ampère's law, Stokes' theorem is applied to the magnetic field, :
Notes
References
{{Reflist Electromagnetism Mechanics Vectors (mathematics and physics) Vector calculus