shallow water equations

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations (or parabolic if viscous shear is considered) that describe the flow below a pressure surface in a fluid (sometimes, but not necessarily, a free surface). The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant (see the related section below).

The equations are derived from depth-integrating the Navier–Stokes equations, in the case where the horizontal length scale is much greater than the vertical length scale. Under this condition, conservation of mass implies that the vertical velocity scale of the fluid is small compared to the horizontal velocity scale. It can be shown from the momentum equation that vertical pressure gradients are nearly hydrostatic, and that horizontal pressure gradients are due to the displacement of the pressure surface, implying that the horizontal velocity field is constant throughout the depth of the fluid. Vertically integrating allows the vertical velocity to be removed from the equations. The shallow-water equations are thus derived.

While a vertical velocity term is not present in the shallow-water equations, note that this velocity is not necessarily zero. This is an important distinction because, for example, the vertical velocity cannot be zero when the floor changes depth, and thus if it were zero only flat floors would be usable with the shallow-water equations. Once a solution (i.e. the horizontal velocities and free surface displacement) has been found, the vertical velocity can be recovered via the continuity equation.

Situations in fluid dynamics where the horizontal length scale is much greater than the vertical length scale are common, so the shallow-water equations are widely applicable. They are used with Coriolis forces in atmospheric and oceanic modeling, as a simplification of the primitive equations of atmospheric flow.

Shallow-water equation models have only one vertical level, so they cannot directly encompass any factor that varies with height. However, in cases where the mean state is sufficiently simple, the vertical variations can be separated from the horizontal and several sets of shallow-water equations can describe the state.

Equations

Conservative form

The shallow-water equations are derived from equations of conservation of mass and conservation of linear momentum (the Navier–Stokes equations), which hold even when the assumptions of shallow-water break down, such as across a hydraulic jump. In the case of a horizontal bed, with negligible Coriolis forces, frictional and viscous forces, the shallow-water equations are:
\begin
\frac &+ \frac + \frac = 0,\\ pt\frac &+ \frac\left( \rho \eta u^2 + \frac\rho g \eta^2 \right) + \frac = 0,\\ pt\frac &+ \frac + \frac\left(\rho \eta v^2 + \frac\rho g \eta ^2\right) = 0.
\end

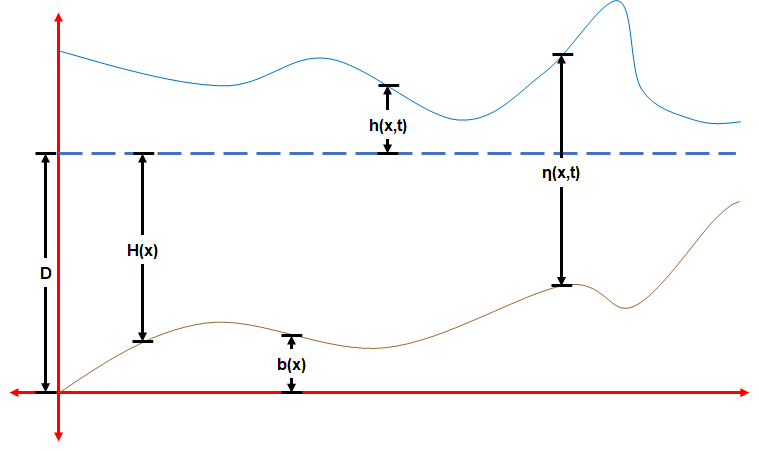
Here ''η'' is the total fluid column height (instantaneous fluid depth as a function of ''x'', ''y'' and ''t''), and the 2D vector (''u'',''v'') is the fluid's horizontal flow velocity, averaged across the vertical column. Further ''g'' is acceleration due to gravity and ρ is the fluid density. The first equation is derived from mass conservation, the second two from momentum conservation.

Non-conservative form

Expanding the derivatives in the above using the product rule, the non-conservative form of the shallow-water equations is obtained. Since velocities are not subject to a fundamental conservation equation, the non-conservative forms do not hold across a shock or hydraulic jump. Also included are the appropriate terms for Coriolis, frictional and viscous forces, to obtain (for constant fluid density):
\begin
\frac &+ \frac \Bigl( (H+h) u \Bigr) + \frac \Bigl( (H+h) v \Bigr) = 0,\\ pt\frac &+ u\frac + v\frac - f v = -g \frac - k u + \nu \left( \frac + \frac \right),\\ pt\frac &+ u\frac + v\frac + f u = -g \frac - k v + \nu \left( \frac + \frac \right),
\end

where

It is often the case that the terms quadratic in ''u'' and ''v'', which represent the effect of bulk advection, are small compared to the other terms. This is called geostrophic balance, and is equivalent to saying that the Rossby number is small. Assuming also that the wave height is very small compared to the mean height (), we have (without lateral viscous forces):
\begin
\frac &+ H \left( \frac + \frac \right) = 0,\\ pt\frac &- f v = -g \frac - b u,\\ pt\frac &+ f u = -g \frac - b v.
\end

One-dimensional Saint-Venant equations

The one-dimensional (1-D) Saint-Venant equations were derived by Adhémar Jean Claude Barré de Saint-Venant, and are commonly used to model transient open-channel flow and surface runoff. They can be viewed as a contraction of the two-dimensional (2-D) shallow-water equations, which are also known as the two-dimensional Saint-Venant equations. The 1-D Saint-Venant equations contain to a certain extent the main characteristics of the channel cross-sectional shape.

The 1-D equations are used extensively in computer models such as TUFLOW, Mascaret (EDF)
SIC (Irstea)
HEC-RAS, SWMM5, ISIS, InfoWorks, Flood Modeller, SOBEK 1DFlow, MIKE 11, and MIKE SHE because they are significantly easier to solve than the full shallow-water equations. Common applications of the 1-D Saint-Venant equations include flood routing along rivers (including evaluation of measures to reduce the risks of flooding), dam break analysis, storm pulses in an open channel, as well as storm runoff in overland flow.

Equations

The system of partial differential equations which describe the 1-D incompressible flow in an open channel of arbitrary cross section – as derived and posed by Saint-Venant in his 1871 paper (equations 19 & 20) – is:

and

where ''x'' is the space coordinate along the channel axis, ''t'' denotes time, ''A''(''x'',''t'') is the cross-sectional area of the flow at location ''x'', ''u''(''x'',''t'') is the flow velocity, ''ζ''(''x'',''t'') is the free surface elevation and τ(''x'',''t'') is the wall shear stress along the wetted perimeter ''P''(''x'',''t'') of the cross section at ''x''. Further ρ is the (constant) fluid density and ''g'' is the gravitational acceleration.

Closure of the hyperbolic system of equations ()–() is obtained from the geometry of cross sections – by providing a functional relationship between the cross-sectional area ''A'' and the surface elevation ζ at each position ''x''. For example, for a rectangular cross section, with constant channel width ''B'' and channel bed elevation ''z''_b, the cross sectional area is: . The instantaneous water depth is , with ''z''_b(''x'') the bed level (i.e. elevation of the lowest point in the bed above datum, see the cross-section figure). For non-moving channel walls the cross-sectional area ''A'' in equation () can be written as:
$A(x,t) = \int_0^ b(x,h')\, dh',$
with ''b''(''x'',''h'') the effective width of the channel cross section at location ''x'' when the fluid depth is ''h'' – so for rectangular channels.

The wall shear stress ''τ'' is dependent on the flow velocity ''u'', they can be related by using e.g. the Darcy–Weisbach equation, Manning formula or Chézy formula.

Further, equation () is the continuity equation, expressing conservation of water volume for this incompressible homogeneous fluid. Equation () is the momentum equation, giving the balance between forces and momentum change rates.

The bed slope ''S''(''x''), friction slope ''S''_f(''x'', ''t'') and hydraulic radius ''R''(''x'', ''t'') are defined as:
$S = - \frac,$
$S_\mathrm = \frac$
and
$R = \frac.$

Consequently, the momentum equation () can be written as: Chow, Ven Te (1959), ''Open-channel hydraulics'', McGraw-Hill, , §18-1 & §18-2.

Conservation of momentum

The momentum equation () can also be cast in the so-called conservation form, through some algebraic manipulations on the Saint-Venant equations, () and (). In terms of the discharge :Cunge, J. A., F. M. Holly Jr. and A. Verwey (1980), ''Practical aspects of computational river hydraulics'', Pitman Publishing, , §§2.1 & 2.2

where ''A'', ''I''₁ and ''I''₂ are functions of the channel geometry, described in the terms of the channel width ''B''(σ,''x''). Here σ is the height above the lowest point in the cross section at location ''x'', see the cross-section figure. So σ is the height above the bed level ''z''_b(''x'') (of the lowest point in the cross section):
$\begin A(\sigma,x) &= \int_0^\sigma B(\sigma', x)\; \mathrm\sigma', \\ I_1(\sigma,x) &= \int_0^\sigma ( \sigma - \sigma' )\, B(\sigma^\prime,x)\; \mathrm\sigma' \qquad \text \\ I_2(\sigma,x) &= \int_0^\sigma ( \sigma - \sigma' )\, \frac\; \mathrm\sigma'. \end$

Above – in the momentum equation () in conservation form – ''A'', ''I''₁ and ''I''₂ are evaluated at . The term describes the hydrostatic force in a certain cross section. And, for a non-prismatic channel, gives the effects of geometry variations along the channel axis ''x''.

In applications, depending on the problem at hand, there often is a preference for using either the momentum equation in non-conservation form, () or (), or the conservation form (). For instance in case of the description of hydraulic jumps, the conservation form is preferred since the momentum flux is continuous across the jump.

Characteristics

The Saint-Venant equations ()–() can be analysed using the method of characteristics. The two celerities d''x''/d''t'' on the characteristic curves are:
$\frac = u \pm c,$ with $c = \sqrt.$

The Froude number determines whether the flow is subcritical () or supercritical ().

For a rectangular and prismatic channel of constant width ''B'', i.e. with and , the Riemann invariants are:
$r_+ = u + 2\sqrt$ and $r_- = u - 2\sqrt,$
so the equations in characteristic form are: Whitham, G. B. (1974) ''Linear and Nonlinear Waves'', §§5.2 & 13.10, Wiley,
$\begin &\frac \left( u + 2 \sqrt \right) = g \left( S - S_f \right) &&\text \quad \frac = u + \sqrt \quad \text \\ &\frac \left( u - 2 \sqrt \right) = g \left( S - S_f \right) &&\text \quad \frac = u - \sqrt. \end$

The Riemann invariants and method of characteristics for a prismatic channel of arbitrary cross-section are described by Didenkulova & Pelinovsky (2011).

The characteristics and Riemann invariants provide important information on the behavior of the flow, as well as that they may be used in the process of obtaining (analytical or numerical) solutions.

Derived modelling

Dynamic wave

The dynamic wave is the full one-dimensional Saint-Venant equation. It is numerically challenging to solve, but is valid for all channel flow scenarios. The dynamic wave is used for modeling transient storms in modeling programs including Mascaret (EDF)
SIC (Irstea)
HEC-RAS
InfoWorks_ICM
MIKE 11, Wash 123d and SWMM5.

In the order of increasing simplifications, by removing some terms of the full 1D Saint-Venant equations (aka Dynamic wave equation), we get the also classical Diffusive wave equation and Kinematic wave equation.

Diffusive wave

For the diffusive wave it is assumed that the inertial terms are less than the gravity, friction, and pressure terms. The diffusive wave can therefore be more accurately described as a non-inertia wave, and is written as:
$g \frac + g (S_f - S) = 0.$

The diffusive wave is valid when the inertial acceleration is much smaller than all other forms of acceleration, or in other words when there is primarily subcritical flow, with low Froude values. Models that use the diffusive wave assumption include MIKE SHE and LISFLOOD-FP. In th
SIC (Irstea)
software this options is also available, since the 2 inertia terms (or any of them) can be removed in option from the interface.

Kinematic wave

For the kinematic wave it is assumed that the flow is uniform, and that the friction slope is approximately equal to the slope of the channel. This simplifies the full Saint-Venant equation to the kinematic wave:
$S_f - S = 0.$

The kinematic wave is valid when the change in wave height over distance and velocity over distance and time is negligible relative to the bed slope, e.g. for shallow flows over steep slopes. The kinematic wave is used in HEC-HMS.

Derivation from Navier–Stokes equations

The 1-D Saint-Venant momentum equation can be derived from the Navier–Stokes equations that describe fluid motion. The ''x''-component of the Navier–Stokes equations – when expressed in Cartesian coordinates in the ''x''-direction – can be written as:
$\frac + u \frac + v \frac+ w \frac= -\frac \frac + \nu \left(\frac + \frac + \frac\right)+ f_x,$

where ''u'' is the velocity in the ''x''-direction, ''v'' is the velocity in the ''y''-direction, ''w'' is the velocity in the ''z''-direction, ''t'' is time, ''p'' is the pressure, ρ is the density of water, ν is the kinematic viscosity, and ''f''_x is the body force in the ''x''-direction.

# If it is assumed that friction is taken into account as a body force, then $\nu$ can be assumed as zero so: $\nu \left(\frac + \frac + \frac\right)= 0.$
# Assuming one-dimensional flow in the ''x''-direction it follows that: $v\frac+ w \frac = 0$
# Assuming also that the pressure distribution is approximately hydrostatic it follows that: $p = \rho g h$ or in differential form: $\partial p = \rho g (\partial h).$ And when these assumptions are applied to the ''x''-component of the Navier–Stokes equations: $-\frac \frac = -\frac\frac = -g \frac.$
# There are 2 body forces acting on the channel fluid, namely, gravity and friction: $f_x =f_ + f_$ where ''f''_x,g is the body force due to gravity and ''f''_x,f is the body force due to friction.
# ''f''_''x'',''g'' can be calculated using basic physics and trigonometry: $F_ = \sin(\theta) gM$where ''F''_g is the force of gravity in the ''x''-direction, ''θ'' is the angle, and ''M'' is the mass. The expression for sin θ can be simplified using trigonometry as: $\sin\theta = \frac.$ For small ''θ'' (reasonable for almost all streams) it can be assumed that: $\sin\theta = \tan\theta = \frac = S$ and given that ''f''_''x'' represents a force per unit mass, the expression becomes: $f_ = gS.$
# Assuming the energy grade line is not the same as the channel slope, and for a reach of consistent slope there is a consistent friction loss, it follows that: $f_ = S_f g.$
# All of these assumptions combined arrives at the 1-dimensional Saint-Venant equation in the ''x''-direction: $\frac + u \frac + g \frac + g (S_f - S) = 0,$ $(a)\quad \ \ (b)\quad \ \ \ (c) \qquad \ \ \ (d) \quad (e)\$ where (a) is the local acceleration term, (b) is the convective acceleration term, (c) is the pressure gradient term, (d) is the friction term, and (e) is the gravity term.

;Terms
The local acceleration (a) can also be thought of as the "unsteady term" as this describes some change in velocity over time. The convective acceleration (b) is an acceleration caused by some change in velocity over position, for example the speeding up or slowing down of a fluid entering a constriction or an opening, respectively. Both these terms make up the inertia terms of the 1-dimensional Saint-Venant equation.

The pressure gradient term (c) describes how pressure changes with position, and since the pressure is assumed hydrostatic, this is the change in head over position. The friction term (d) accounts for losses in energy due to friction, while the gravity term (e) is the acceleration due to bed slope.

Wave modelling by shallow-water equations

Shallow-water equations can be used to model Rossby and Kelvin waves in the atmosphere, rivers, lakes and oceans as well as gravity waves in a smaller domain (e.g. surface waves in a bath). In order for shallow-water equations to be valid, the wavelength of the phenomenon they are supposed to model has to be much larger than the depth of the basin where the phenomenon takes place. Somewhat smaller wavelengths can be handled by extending the shallow-water equations using the Boussinesq approximation to incorporate dispersion effects. Shallow-water equations are especially suitable to model tides which have very large length scales (over hundred of kilometers). For tidal motion, even a very deep ocean may be considered as shallow as its depth will always be much smaller than the tidal wavelength.

Turbulence modelling using non-linear shallow-water equations

Shallow-water equations, in its non-linear form, is an obvious candidate for modelling turbulence in the atmosphere and oceans, i.e. geophysical turbulence. An advantage of this, over Quasi-geostrophic equations, is that it allows solutions like gravity waves, while also conserving energy and potential vorticity. However there are also some disadvantages as far as geophysical applications are concerned - it has a non-quadratic expression for total energy and a tendency for waves to become shock waves. Some alternate models have been proposed which prevent shock formation. One alternative is to modify the "pressure term" in the momentum equation, but it results in a complicated expression for kinetic energy. Another option is to modify the non-linear terms in all equations, which gives a quadratic expression for kinetic energy, avoids shock formation, but conserves only linearized potential vorticity.

See also

*Waves and shallow water

Notes

Further reading

*
*
*

External links

Derivation of the shallow-water equations from first principles
(instead of simplifying the Navier–Stokes equations, some analytical solutions)

{{physical oceanography

Equations of fluid dynamics
Partial differential equations
Physical oceanography
Water waves