Supertoroid

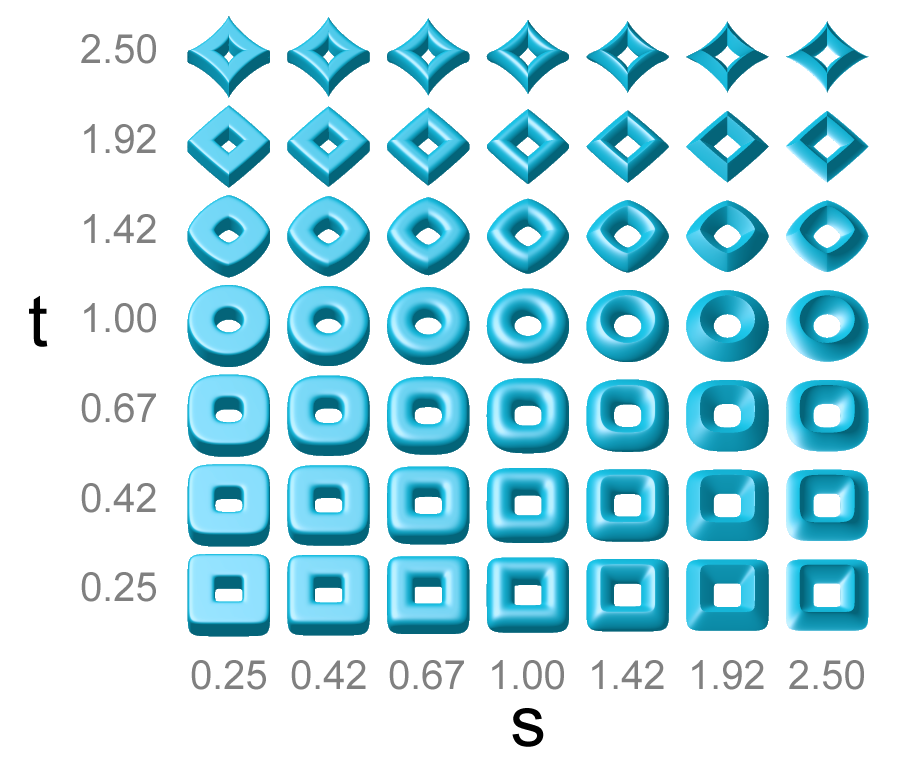In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces (technically, a topological torus) whose shape is defined by mathematical formulas similar to those that define the superellipsoids. The plural of "supertorus" is either supertori or supertoruses.

The family was described and named by Alan Barr in 1994.Alan H. Barr (1981) ''Superquadrics and Angle-Preserving Transformations''. IEEE Computer Graphics and Applications, volume 1 issue 1. pp. 11-23.

Barr's supertoroids have been fairly popular in computer graphics as a convenient model for many objects, such as smooth frames for rectangular things. One quarter of a supertoroid can provide a smooth and seamless 90-degree joint between two superquadric cylinders. However, they are not algebraic surfaces (except in special cases).

Formulas

Alan Barr's supertoroids are defined by parametric equations similar to the trigonometric equations of the torus, except that the sine and cosine terms are raised to arbitrary powers. Namely, the generic point of the surface is given by
$P(u,v) = \left(\begin X(u,v)\\ Y(u,v)\\ Z(u,v) \end\right) = \left(\begin (a + C_^) C_^\\ (b + C_^) S_^\\ S_^ \end\right)$
where
$\begin C_\theta^\varepsilon &= \operatorname(\cos \theta) \, \left, \, \cos\theta \, \^\varepsilon, \\ S_\theta^\varepsilon &= \operatorname(\sin \theta) \ \left, \, \sin\theta \ \^\varepsilon, \end$
is the sign function, and the parameters range from 0 to 360 degrees (0 to 2''π'' radians).

In these formulas, the parameter controls the "squareness" of the vertical sections, controls the squareness of the horizontal sections, and are the major radii in the and directions. With and one obtains the ordinary torus with major radius and minor radius 1, with the center at the origin and rotational symmetry about the -axis.

In general, the supertorus defined as above spans the intervals:
\begin
-(a+1) &\leq& x &\leq& +(a+1) \\ pt -(b+1) &\leq& y &\leq& +(b+1) \\ pt -1 &\leq& z &\leq& +1
\end
The whole shape is symmetric about the planes , , and . The hole runs in the direction and spans the intervals
\begin
-(a-1) &\leq& x &\leq& +(a-1) \\ pt -(b-1) &\leq& y &\leq& +(b-1) \\ pt -\infty &\leq& z &\leq& +\infty
\end

A curve of constant on this surface is a horizontal Lamé curve with exponent scaled in and and displaced in . A curve of constant , projected on the plane or , is a Lamé curve with exponent scaled and horizontally shifted. If , the curve is planar and spans the intervals:
\begin
a-1 &\leq& x &\leq& a+1 \\ pt -1 &\leq& z &\leq& +1
\end
and similarly if . The curve is also planar if .

In general, if and is not a multiple of 90 degrees, the curve of constant will not be planar; and, conversely, a vertical plane section of the supertorus will not be a Lamé curve.

The basic supertoroid shape defined above is often modified by non-uniform scaling to yield supertoroids of specific width, length, and vertical thickness.

Plotting code

The following GNU Octave code generates plots of a supertorus:

function supertoroid(epsilon,a)
n=50;
d=.1;
etamax=pi;
etamin=-pi;
wmax=pi;
wmin=-pi;
deta=(etamax-etamin)/n;
dw=(wmax-wmin)/n;
k=0;
l=0;
for i=1:n+1
eta(i)=etamin+(i-1)*deta;
for j=1:n+1
w(j)=wmin+(j-1)*dw;
x(i,j)=a(1)*(a(4)+sign(cos(eta(i)))*abs(cos(eta(i)))^epsilon(1))*sign(cos(w(j)))*abs(cos(w(j)))^epsilon(2);
y(i,j)=a(2)*(a(4)+sign(cos(eta(i)))*abs(cos(eta(i)))^epsilon(1))*sign(sin(w(j)))*abs(sin(w(j)))^epsilon(2);
z(i,j)=a(3)*sign(sin(eta(i)))*abs(sin(eta(i)))^epsilon(1);
endfor;
endfor;
mesh(x,y,z);
endfunction;

See also

* Superellipsoid
* Superegg
* Superquadric

References

{{Reflist

Surfaces
Computer graphics