Super-root on:
[Wikipedia]
[Google]
[Amazon]
 In
In
An Investigation of Arithmetic Operations.
Retrieved 9 January 2019. however, unlike the operations before it, tetration is not an

 Since
Since
 Tetration can be extended to infinite heights; i.e., for certain and values in , there exists a well defined result for an infinite . This is because for bases within a certain interval, tetration converges to a finite value as the height tends to
Tetration can be extended to infinite heights; i.e., for certain and values in , there exists a well defined result for an infinite . This is because for bases within a certain interval, tetration converges to a finite value as the height tends to
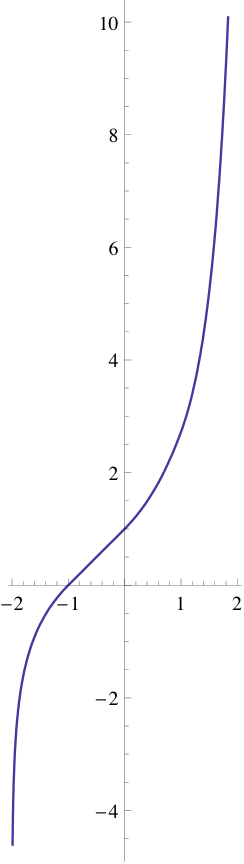 A linear approximation (solution to the continuity requirement, approximation to the differentiability requirement) is given by:
:
hence:
and so on. However, it is only piecewise differentiable; at integer values of , the derivative is multiplied by . It is continuously differentiable for if and only if . For example, using these methods and
A main theorem in Hooshmand's paper states: Let . If is continuous and satisfies the conditions:
*
* is differentiable on ,
* is a nondecreasing or nonincreasing function on ,
*
then is uniquely determined through the equation
:
where
A linear approximation (solution to the continuity requirement, approximation to the differentiability requirement) is given by:
:
hence:
and so on. However, it is only piecewise differentiable; at integer values of , the derivative is multiplied by . It is continuously differentiable for if and only if . For example, using these methods and
A main theorem in Hooshmand's paper states: Let . If is continuous and satisfies the conditions:
*
* is differentiable on ,
* is a nondecreasing or nonincreasing function on ,
*
then is uniquely determined through the equation
:
where
 In
In mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
. There is no standard notation
In linguistics and semiotics, a notation system is a system of graphics or symbols, Character_(symbol), characters and abbreviated Expression (language), expressions, used (for example) in Artistic disciplines, artistic and scientific disciplines ...
for tetration, though Knuth's up arrow notation and the left-exponent are common.
Under the definition as repeated exponentiation, means , where ' copies of ' are iterated via exponentiation, right-to-left, i.e. the application of exponentiation times. ' is called the "height" of the function, while ' is called the "base," analogous to exponentiation. It would be read as "the th tetration of ". For example, 2 tetrated to 4 (or the fourth tetration of 2) is .
It is the next hyperoperation
In mathematics, the hyperoperation sequence is an infinite sequence of arithmetic operations (called ''hyperoperations'' in this context) that starts with a unary operation (the successor function with ''n'' = 0). The sequence continues with th ...
after exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
, but before pentation
In mathematics, pentation (or hyper-5) is the fifth hyperoperation. Pentation is defined to be repeated tetration, similarly to how tetration is repeated exponentiation, exponentiation is repeated multiplication, and multiplication is repeated add ...
. The word was coined by Reuben Louis Goodstein from tetra-
Numeral or number prefixes are prefixes derived from numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example:
* triangle, quadrilateral, pentagon, hexagon, o ...
(four) and iteration
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration.
...
.
Tetration is also defined recursively as
:
allowing for the holomorphic
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex deri ...
extension of tetration to non-natural numbers such as real, complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
, and ordinal number
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals (first, second, th, etc.) aimed to extend enumeration to infinite sets.
A finite set can be enumerated by successively labeling each element with the leas ...
s, which was proved in 2017.
The two inverses of tetration are called super-root
In mathematics, tetration (or hyper-4) is an operation (mathematics), operation based on iterated, or repeated, exponentiation. There is no standard mathematical notation, notation for tetration, though Knuth's up arrow notation \uparrow \upa ...
and super-logarithm, analogous to the nth root
In mathematics, an th root of a number is a number which, when raised to the power of , yields : r^n = \underbrace_ = x.
The positive integer is called the ''index'' or ''degree'', and the number of which the root is taken is the ''ra ...
and the logarithmic functions. None of the three functions are elementary.
Tetration is used for the notation of very large numbers.
Introduction
The first fourhyperoperation
In mathematics, the hyperoperation sequence is an infinite sequence of arithmetic operations (called ''hyperoperations'' in this context) that starts with a unary operation (the successor function with ''n'' = 0). The sequence continues with th ...
s are shown here, with tetration being considered the fourth in the series. The unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. This is in contrast to ''binary operations'', which use two operands. An example is any function , where is a set; the function is a unary operation ...
succession
Succession is the act or process of following in order or sequence.
Governance and politics
*Order of succession, in politics, the ascension to power by one ruler, official, or monarch after the death, resignation, or removal from office of ...
, defined as , is considered to be the zeroth operation.
#Addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
copies of 1 added to combined by succession.
#Multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
copies of combined by addition.
#Exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
copies of combined by multiplication.
#Tetration copies of combined by exponentiation, right-to-left.
Importantly, nested exponents are interpreted from the top down: means and not
Succession, , is the most basic operation; while addition () is a primary operation, for addition of natural numbers it can be thought of as a chained succession of successors of ; multiplication () is also a primary operation, though for natural numbers it can analogously be thought of as a chained addition involving numbers of . Exponentiation can be thought of as a chained multiplication involving numbers of and tetration () as a chained power involving numbers . Each of the operations above are defined by iterating the previous one;Neyrinck, MarkAn Investigation of Arithmetic Operations.
Retrieved 9 January 2019. however, unlike the operations before it, tetration is not an
elementary function
In mathematics, an elementary function is a function of a single variable (typically real or complex) that is defined as taking sums, products, roots and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, a ...
.
The parameter is referred to as the base, while the parameter may be referred to as the height. In the original definition of tetration, the height parameter must be a natural number; for instance, it would be illogical to say "three raised to itself negative five times" or "four raised to itself one half of a time." However, just as addition, multiplication, and exponentiation can be defined in ways that allow for extensions to real and complex numbers, several attempts have been made to generalize tetration to negative numbers, real numbers, and complex numbers. One such way for doing so is using a recursive definition for tetration; for any positive real and non-negative integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
, we can define recursively as:
:
The recursive definition is equivalent to repeated exponentiation for natural
Nature is an inherent character or constitution, particularly of the ecosphere or the universe as a whole. In this general sense nature refers to the laws, elements and phenomena of the physical world, including life. Although humans are part ...
heights; however, this definition allows for extensions to the other heights such as , , and as well – many of these extensions are areas of active research.
Terminology
There are many terms for tetration, each of which has some logic behind it, but some have not become commonly used for one reason or another. Here is a comparison of each term with its rationale and counter-rationale. * The term ''tetration'', introduced by Goodstein in his 1947 paper ''Transfinite Ordinals in Recursive Number Theory'' (generalizing the recursive base-representation used inGoodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, proved by Reuben Goodstein in 1944, which states that every Goodstein sequence (as defined below) eventually terminates at 0. Laurence Kirby and Jeff Paris showed ...
to use higher operations), has gained dominance. It was also popularized in Rudy Rucker
Rudolf von Bitter Rucker (; born March 22, 1946) is an American mathematician, computer scientist, science fiction author, and one of the founders of the cyberpunk literary movement. The author of both fiction and non-fiction, he is best known f ...
's '' Infinity and the Mind''.
* The term ''superexponentiation'' was published by Bromer in his paper ''Superexponentiation'' in 1987. It was used earlier by Ed Nelson in his book Predicative Arithmetic, Princeton University Press
Princeton University Press is an independent publisher with close connections to Princeton University. Its mission is to disseminate scholarship within academia and society at large.
The press was founded by Whitney Darrow, with the financial ...
, 1986.
* The term ''hyperpower'' is a natural combination of ''hyper'' and ''power'', which aptly describes tetration. The problem lies in the meaning of ''hyper'' with respect to the hyperoperation
In mathematics, the hyperoperation sequence is an infinite sequence of arithmetic operations (called ''hyperoperations'' in this context) that starts with a unary operation (the successor function with ''n'' = 0). The sequence continues with th ...
sequence. When considering hyperoperations, the term ''hyper'' refers to all ranks, and the term ''super'' refers to rank 4, or tetration. So under these considerations ''hyperpower'' is misleading, since it is only referring to tetration.
* The term ''power tower'' is occasionally used, in the form "the power tower of order " for . Exponentiation is easily misconstrued: note that the operation of raising to a power is right-associative (see below
Below may refer to:
*Earth
*Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
* Ernst von Below (1863–1955), German World War I general
* Fred Belo ...
). Tetration is iterated ''exponentiation'' (call this right-associative
In programming language theory, the associativity of an operator is a property that determines how operators of the same precedence are grouped in the absence of parentheses. If an operand is both preceded and followed by operators (for examp ...
operation ^), starting from the top right side of the expression with an instance a^a (call this value c). Exponentiating the next leftward a (call this the 'next base' b), is to work leftward after obtaining the new value b^c. Working to the left, use the next a to the left, as the base b, and evaluate the new b^c. 'Descend down the tower' in turn, with the new value for c on the next downward step.
Owing in part to some shared terminology and similar notational symbolism, tetration is often confused with closely related functions and expressions. Here are a few related terms:
In the first two expressions is the ''base'', and the number of times appears is the ''height'' (add one for ). In the third expression, is the ''height'', but each of the bases is different.
Care must be taken when referring to iterated exponentials, as it is common to call expressions of this form iterated exponentiation, which is ambiguous, as this can either mean iterated powers or iterated exponentials
Exponential may refer to any of several mathematical topics related to exponentiation, including:
*Exponential function, also:
**Matrix exponential, the matrix analogue to the above
*Exponential decay, decrease at a rate proportional to value
*Expo ...
.
Notation
There are many different notation styles that can be used to express tetration. Some notations can also be used to describe otherhyperoperation
In mathematics, the hyperoperation sequence is an infinite sequence of arithmetic operations (called ''hyperoperations'' in this context) that starts with a unary operation (the successor function with ''n'' = 0). The sequence continues with th ...
s, while some are limited to tetration and have no immediate extension.
One notation above uses iterated exponential notation; this is defined in general as follows:
: with s.
There are not as many notations for iterated exponentials, but here are a few:
Examples
Because of the extremely fast growth of tetration, most values in the following table are too large to write inscientific notation
Scientific notation is a way of expressing numbers that are too large or too small to be conveniently written in decimal form, since to do so would require writing out an inconveniently long string of digits. It may be referred to as scientif ...
. In these cases, iterated exponential notation is used to express them in base 10. The values containing a decimal point are approximate. Usually, the limit that can be calculated in a numerical calculation program such as Wolfram Alpha
WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data.
History
Launch preparations for WolframAlpha began on Ma ...
is 3↑↑4, and the number of digits up to 3↑↑5 can be expressed.
Remark: If does not differ from 10 by orders of magnitude, then for all . For example, in the above table, and the difference is even smaller for the following rows.
Extensions
Tetration can be extended in two different ways; in the equation , both the base and the height can be generalized using the definition and properties of tetration. Although the base and the height can be extended beyond the non-negative integers to different domains, including , complex functions such as , and heights of infinite , the more limited properties of tetration reduce the ability to extend tetration.Extension of domain for bases
Base zero
The exponential is not consistently defined. Thus, the tetrations are not clearly defined by the formula given earlier. However, is well defined, and exists: : Thus we could consistently define . This is analogous to defining . Under this extension, , so the rule from the original definition still holds.Complex bases

 Since
Since complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s can be raised to powers, tetration can be applied to ''bases'' of the form (where and are real). For example, in with , tetration is achieved by using the principal branch
In mathematics, a principal branch is a function which selects one branch point, branch ("slice") of a multi-valued function. Most often, this applies to functions defined on the complex plane.
Examples
Trigonometric inverses
Principal bra ...
of the natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
; using Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for ...
we get the relation:
:
This suggests a recursive definition for given any :
:
The following approximate values can be derived:
Solving the inverse relation, as in the previous section, yields the expected and , with negative values of giving infinite results on the imaginary axis. Plotted in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
, the entire sequence spirals to the limit , which could be interpreted as the value where is infinite.
Such tetration sequences have been studied since the time of Euler, but are poorly understood due to their chaotic behavior. Most published research historically has focused on the convergence of the infinitely iterated exponential function. Current research has greatly benefited by the advent of powerful computers with fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
and symbolic mathematics software. Much of what is known about tetration comes from general knowledge of complex dynamics and specific research of the exponential map.
Extensions of the domain for different heights
Infinite heights
infinity
Infinity is something which is boundless, endless, or larger than any natural number. It is denoted by \infty, called the infinity symbol.
From the time of the Ancient Greek mathematics, ancient Greeks, the Infinity (philosophy), philosophic ...
. For example, converges to 2, and can therefore be said to be equal to 2. The trend towards 2 can be seen by evaluating a small finite tower:
:
In general, the infinitely iterated exponential , defined as the limit of as goes to infinity, converges for , roughly the interval from 0.066 to 1.44, a result shown by Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
. The limit, should it exist, is a positive real solution of the equation . Thus, . The limit defining the infinite exponential of does not exist when because the maximum of is . The limit also fails to exist when .
This may be extended to complex numbers with the definition:
:
where represents Lambert's W function.
As the limit (if existent on the positive real line, i.e. for ) must satisfy we see that is (the lower branch of) the inverse function of .
Negative heights
We can use the recursive rule for tetration, : to prove : : Substituting −1 for gives : . Smaller negative values cannot be well defined in this way. Substituting −2 for in the same equation gives : which is not well defined. They can, however, sometimes be considered sets. For , any definition of is consistent with the rule because : for any .Linear approximation for real heights
 A linear approximation (solution to the continuity requirement, approximation to the differentiability requirement) is given by:
:
hence:
and so on. However, it is only piecewise differentiable; at integer values of , the derivative is multiplied by . It is continuously differentiable for if and only if . For example, using these methods and
A main theorem in Hooshmand's paper states: Let . If is continuous and satisfies the conditions:
*
* is differentiable on ,
* is a nondecreasing or nonincreasing function on ,
*
then is uniquely determined through the equation
:
where
A linear approximation (solution to the continuity requirement, approximation to the differentiability requirement) is given by:
:
hence:
and so on. However, it is only piecewise differentiable; at integer values of , the derivative is multiplied by . It is continuously differentiable for if and only if . For example, using these methods and
A main theorem in Hooshmand's paper states: Let . If is continuous and satisfies the conditions:
*
* is differentiable on ,
* is a nondecreasing or nonincreasing function on ,
*
then is uniquely determined through the equation
:
where