stochastic block model

The stochastic block model is a generative model for random graphs. This model tends to produce graphs containing ''communities'', subsets of nodes characterized by being connected with one another with particular edge densities. For example, edges may be more common within communities than between communities. Its mathematical formulation was first introduced in 1983 in the field of social network analysis by Paul W. Holland et al. The stochastic block model is important in statistics, machine learning, and network science, where it serves as a useful benchmark for the task of recovering community structure in graph data.

Definition

The stochastic block model takes the following parameters:
* The number $n$ of vertices;
* a partition of the vertex set $\$ into disjoint subsets $C_1,\ldots,C_r$, called ''communities'';
* a symmetric $r \times r$ matrix $P$ of edge probabilities.

The edge set is then sampled at random as follows: any two vertices $u \in C_i$ and $v \in C_j$ are connected by an edge with probability $P_$. An example problem is: given a graph with $n$ vertices, where the edges are sampled as described, recover the groups $C_1,\ldots,C_r$.

Special cases

If the probability matrix is a constant, in the sense that $P_ = p$ for all $i,j$, then the result is the Erdős–Rényi model $G(n,p)$. This case is degenerate—the partition into communities becomes irrelevant—but it illustrates a close relationship to the Erdős–Rényi model.

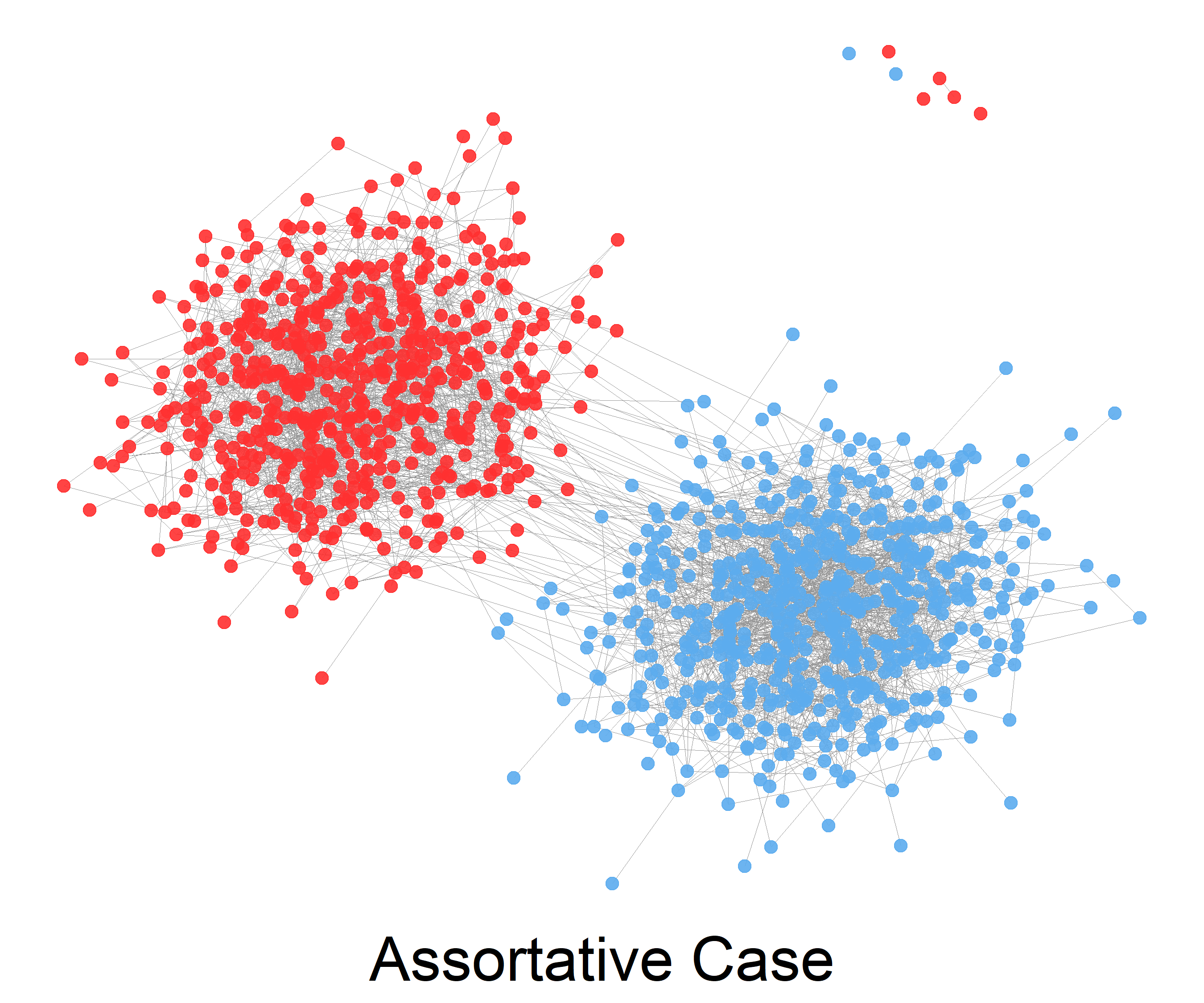
The ''planted partition model'' is the special case that the values of the probability matrix $P$ are a constant $p$ on the diagonal and another constant $q$ off the diagonal. Thus two vertices within the same community share an edge with probability $p$, while two vertices in different communities share an edge with probability $q$. Sometimes it is this restricted model that is called the stochastic block model. The case where $p > q$ is called an ''assortative'' model, while the case $p < q$ is called ''disassortative''.

Returning to the general stochastic block model, a model is called ''strongly assortative'' if $P_ > P_$ whenever $j \neq k$: all diagonal entries dominate all off-diagonal entries. A model is called ''weakly assortative'' if $P_ > P_$ whenever $i \neq j$: each diagonal entry is only required to dominate the rest of its own row and column. ''Disassortative'' forms of this terminology exist, by reversing all inequalities. For some algorithms, recovery might be easier for block models with assortative or disassortative conditions of this form.

Typical statistical tasks

Much of the literature on algorithmic community detection addresses three statistical tasks: detection, partial recovery, and exact recovery.

Detection

The goal of detection algorithms is simply to determine, given a sampled graph, whether the graph has latent community structure. More precisely, a graph might be generated, with some known prior probability, from a known stochastic block model, and otherwise from a similar Erdos-Renyi model. The algorithmic task is to correctly identify which of these two underlying models generated the graph.

Partial recovery

In partial recovery, the goal is to approximately determine the latent partition into communities, in the sense of finding a partition that is correlated with the true partition significantly better than a random guess.

Exact recovery

In exact recovery, the goal is to recover the latent partition into communities exactly. The community sizes and probability matrix may be known or unknown.

Statistical lower bounds and threshold behavior

Stochastic block models exhibit a sharp threshold effect reminiscent of percolation thresholds. Suppose that we allow the size $n$ of the graph to grow, keeping the community sizes in fixed proportions. If the probability matrix remains fixed, tasks such as partial and exact recovery become feasible for all non-degenerate parameter settings. However, if we scale down the probability matrix at a suitable rate as $n$ increases, we observe a sharp phase transition: for certain settings of the parameters, it will become possible to achieve recovery with probability tending to 1, whereas on the opposite side of the parameter threshold, the probability of recovery tends to 0 no matter what algorithm is used.

For partial recovery, the appropriate scaling is to take $P_ = \tilde P_ / n$ for fixed $\tilde P$, resulting in graphs of constant average degree. In the case of two equal-sized communities, in the assortative planted partition model with probability matrix
$P = \left(\begin \tilde p/n & \tilde q/n \\ \tilde q/n & \tilde p/n \end \right),$
partial recovery is feasible with probability $1 - o(1)$ whenever $(\tilde p - \tilde q)^2 > 2(\tilde p + \tilde q)$, whereas any estimator fails partial recovery with probability $1-o(1)$ whenever $(\tilde p - \tilde q)^2 < 2(\tilde p + \tilde q)$.

For exact recovery, the appropriate scaling is to take $P_ = \tilde P_ \log n / n$, resulting in graphs of logarithmic average degree. Here a similar threshold exists: for the assortative planted partition model with $r$ equal-sized communities, the threshold lies at $\sqrt - \sqrt = \sqrt$. In fact, the exact recovery threshold is known for the fully general stochastic block model.

Algorithms

In principle, exact recovery can be solved in its feasible range using maximum likelihood, but this amounts to solving a constrained or regularized cut problem such as minimum bisection that is typically NP-complete. Hence, no known efficient algorithms will correctly compute the maximum-likelihood estimate in the worst case.

However, a wide variety of algorithms perform well in the average case, and many high-probability performance guarantees have been proven for algorithms in both the partial and exact recovery settings. Successful algorithms include spectral clustering of the vertices, semidefinite programming, forms of belief propagation, and community detection among others.

Variants

Several variants of the model exist. One minor tweak allocates vertices to communities randomly, according to a categorical distribution, rather than in a fixed partition. More significant variants include the degree-corrected stochastic block model, the hierarchical stochastic block model, the geometric block model, censored block model and the mixed-membership block model.

Topic models

Stochastic block model have been recognised to be a topic model on bipartite networks. In a network of documents and words, Stochastic block model can identify topics: group of words with a similar meaning.

Extensions to signed graphs

Signed graphs allow for both favorable and adverse relationships and serve as a common model choice for various data analysis applications, e.g., correlation clustering. The stochastic block model can be trivially extended to signed graphs by assigning both positive and negative edge weights or equivalently using a difference of adjacency matrices of two stochastic block models.

DARPA/MIT/AWS Graph Challenge: streaming stochastic block partition

GraphChallenge encourages community approaches to developing new solutions for analyzing graphs and sparse data derived from social media, sensor feeds, and scientific data to enable relationships between events to be discovered as they unfold in the field. Streaming stochastic block partition is one of the challenges since 2017.
Spectral clustering has demonstrated outstanding performance compared to the original and even improved
base algorithm, matching its quality of clusters while being multiple orders of magnitude faster.

See also

* blockmodeling
*
* for generating benchmark networks with communities

References

{{reflist, refs=
{{cite journal,
last1 = Decelle, first1 = Aurelien ,
last2 = Krzakala, first2 = Florent ,
last3 = Moore, first3 = Cristopher ,
last4 = Zdeborová , first4 = Lenka , author4-link = Lenka Zdeborová ,
title = Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications ,
arxiv = 1109.3041 ,
date = September 2011 , doi=10.1103/PhysRevE.84.066106 , volume=84 , journal=Physical Review E, issue = 6 , bibcode = 2011PhRvE..84f6106D , pmid=22304154 , page=066106, s2cid = 15788070
{{cite arXiv, last1 = Abbe, first1 = Emmanuel, last2 = Bandeira, first2 = Afonso S., last3 = Hall, first3 = Georgina, title = Exact Recovery in the Stochastic Block Model, eprint= 1405.3267, date = May 2014 , class = cs.SI
{{cite arXiv, last1 = Abbe, first1 = Emmanuel, last2 = Sandon, first2 = Colin, title = Community detection in general stochastic block models: fundamental limits and efficient recovery algorithms, eprint= 1503.00609, date = March 2015 , class = math.PR
{{cite arXiv, last1 = Abbe, first1 = Emmanuel, last2 = Sandon, first2 = Colin, title = Recovering communities in the general stochastic block model without knowing the parameters, eprint= 1506.03729, date = June 2015 , class = math.PR
{{Cite journal, doi = 10.1214/14-AOS1274, issn = 0090-5364, volume = 43, issue = 1, pages = 215–237, last1 = Lei, first1 = Jing, last2 = Rinaldo, first2 = Alessandro, title = Consistency of spectral clustering in stochastic block models, journal = The Annals of Statistics, date = February 2015 , arxiv = 1312.2050, s2cid = 88519551
{{Cite journal, last1 = Galhotra, first1 = Sainyam, last2 = Mazumdar, first2 = Arya, last3 = Pal, first3 = Soumyabrata,
last4 = Saha, first4 = Barna, author4-link=Barna Saha, title = The Geometric Block Model, journal = AAAI, date = February 2018 , volume = 32, doi = 10.1609/aaai.v32i1.11905, arxiv = 1709.05510, s2cid = 19152144
{{cite journal,
last1 = Krzakala, first1 = Florent,
last2 = Moore, first2 = Cristopher,
last3 = Mossel, first3 = Elchanan,
last4 = Neeman, first4 = Joe,
last5 = Sly, first5 = Allan,
last6 = Lenka, first6 = Lenka,
last7 = Zhang, first7 = Pan,
title = Spectral redemption in clustering sparse networks , journal = Proceedings of the National Academy of Sciences, date = October 2013 , doi = 10.1073/pnas.1312486110 , arxiv = 1306.5550, bibcode = 2013PNAS..11020935K , volume=110 , issue = 52, pages=20935–20940, pmid = 24277835, pmc = 3876200, doi-access = free
{{cite arXiv, last1 = Mossel, first1 = Elchanan, last2 = Neeman, first2 = Joe, last3 = Sly, first3 = Allan, title = Stochastic Block Models and Reconstruction, eprint= 1202.1499, date = February 2012 , class = math.PR
{{cite journal, last1 = Mossel, first1 = Elchanan, last2 = Neeman, first2 = Joe, last3 = Sly, first3 = Allan, title = Belief Propagation, Robust Reconstruction, and Optimal Recovery of Block Models, journal = The Annals of Applied Probability, arxiv= 1309.1380, date = September 2013 , volume = 26, issue = 4, pages = 2211–2256, doi = 10.1214/15-AAP1145, bibcode = 2013arXiv1309.1380M, s2cid = 184446
{{cite arXiv, last = Massoulie, first = Laurent, title = Community detection thresholds and the weak Ramanujan property, eprint= 1311.3085, date = November 2013 , class = cs.SI
{{cite arXiv, last1 = Amini, first1 = Arash A., last2 = Levina, first2 = Elizaveta, author2-link= Elizaveta Levina, title = On semidefinite relaxations for the block model, eprint= 1406.5647, date = June 2014 , class = cs.LG
{{cite journal,
last1 = Airoldi, first1 = Edoardo, authorlink1=Edoardo Airoldi,
last2 = Blei, first2 = David,
last3 = Feinberg, first3 = Stephen,
last4 = Xing, first4 = Eric,
title = Mixed membership stochastic blockmodels, journal = Journal of Machine Learning Research , arxiv = 0705.4485, date = May 2007 , volume = 9, pages = 1981–2014, pmid = 21701698, pmc = 3119541, bibcode = 2007arXiv0705.4485A
{{cite arXiv, last = Fathi, first = Reza, title = Efficient Distributed Community Detection in the Stochastic Block Model, eprint= 1904.07494, date = April 2019 , class = cs.DC
{{cite journal , title=Stochastic blockmodels: First steps , journal=Social Networks , year=1983 , last1=Holland , first1=Paul W , last2=Laskey , first2=Kathryn Blackmond , last3=Leinhardt , first3=Samuel , volume=5 , issue=2 , pages=109–137 , issn=0378-8733 , doi=10.1016/0378-8733(83)90021-7 , s2cid=34098453 , url=https://doi.org/10.1016/0378-8733(83)90021-7 , accessdate=2021-06-16 , archive-date=2023-02-04 , archive-url=https://web.archive.org/web/20230204160405/https://www.sciencedirect.com/science/article/abs/pii/0378873383900217?via%3Dihub , url-status=live
{{cite journal , title=Stochastic blockmodels and community structure in networks , journal=Physical Review E , year=2011 , last1=Karrer , first1=Brian , last2=Newman , first2=Mark E J , volume=83 , issue=1 , page=016107 , doi=10.1103/PhysRevE.83.016107 , pmid=21405744 , url=https://link.aps.org/doi/10.1103/PhysRevE.83.016107 , accessdate=2021-06-16 , arxiv=1008.3926 , bibcode=2011PhRvE..83a6107K , s2cid=9068097 , archive-date=2023-02-04 , archive-url=https://web.archive.org/web/20230204160406/https://journals.aps.org/pre/abstract/10.1103/PhysRevE.83.016107 , url-status=live
{{cite journal , title=Hierarchical block structures and high-resolution model selection in large networks , journal=Physical Review X , year=2014 , last=Peixoto , first=Tiago , volume=4 , issue=1 , page=011047 , doi=10.1103/PhysRevX.4.011047 , url=https://journals.aps.org/prx/abstract/10.1103/PhysRevX.4.011047 , accessdate=2021-06-16 , arxiv=1310.4377 , bibcode=2014PhRvX...4a1047P , s2cid=5841379 , archive-date=2021-06-24 , archive-url=https://web.archive.org/web/20210624195430/https://journals.aps.org/prx/abstract/10.1103/PhysRevX.4.011047 , url-status=live

Random graphs
Networks
Blockmodeling