stellated octahedron on:
[Wikipedia]
[Google]
[Amazon]
 The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in
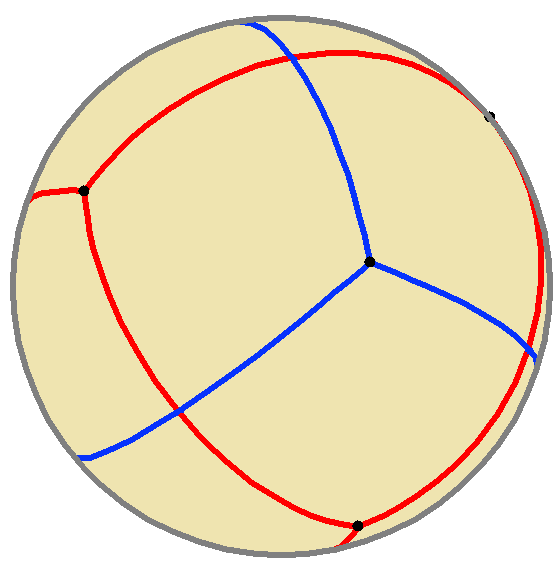
 A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, between two parallel edges of the two tetrahedra. These two tetrahedra can be completed to a
A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, between two parallel edges of the two tetrahedra. These two tetrahedra can be completed to a
 The stellated octahedron appears with several other polyhedra and polyhedral compounds in M. C. Escher's print " Stars", and provides the central form in Escher's ''
The stellated octahedron appears with several other polyhedra and polyhedral compounds in M. C. Escher's print " Stars", and provides the central form in Escher's ''
Pacioli
Fra Luca Bartolomeo de Pacioli (sometimes ''Paccioli'' or ''Paciolo''; 1447 – 19 June 1517) was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and an early contributor to the field now known as accounting ...
's ''De Divina Proportione,'' 1509.
It is the simplest of five regular polyhedral compounds, and the only regular compound of two tetrahedra. It is also the least dense of the regular polyhedral compounds, having a density of 2.
It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells. It can also be seen as one of the stages in the construction of a 3D Koch snowflake, a fractal shape formed by repeated attachment of smaller tetrahedra to each triangular face of a larger figure. The first stage of the construction of the Koch Snowflake is a single central tetrahedron, and the second stage, formed by adding four smaller tetrahedra to the faces of the central tetrahedron, is the stellated octahedron.
Construction
The Cartesian coordinates of the stellated octahedron are as follows: (±1/2, ±1/2, 0) (0, 0, ±1/√2) (±1, 0, ±1/√2) (0, ±1, ±1/√2) The stellated octahedron can be constructed in several ways: *It is a stellation of the regular octahedron, sharing the same face planes. (See Wenninger model W19.) *It is also a regular polyhedron compound, when constructed as the union of two regulartetrahedra
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ...
(a regular tetrahedron and its dual tetrahedron).
*It can be obtained as an augmentation of the regular octahedron, by adding tetrahedral pyramids
A pyramid (from el, πυραμίς ') is a structure whose outer surfaces are triangular and converge to a single step at the top, making the shape roughly a pyramid in the geometric sense. The base of a pyramid can be trilateral, quadrilat ...
on each face. In this construction it has the same topology as the convex Catalan solid, the triakis octahedron, which has much shorter pyramids.
*It is a facetting of the cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the on ...
, sharing the vertex arrangement.
*It can be seen as a antiprism; with being a tetragram, a compound of two dual digons, and the tetrahedron seen as a digonal antiprism, this can be seen as a compound of two digonal antiprism
In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same sha ...
s.
*It can be seen as a net of a four-dimensional octahedral pyramid, consisting of a central octahedron surrounded by eight tetrahedra.
Related concepts
 A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, between two parallel edges of the two tetrahedra. These two tetrahedra can be completed to a
A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, between two parallel edges of the two tetrahedra. These two tetrahedra can be completed to a desmic system
Two desmic tetrahedra. The third tetrahedron of this system is not shown, but has one vertex at the center and the other three on the plane at infinity.
In projective geometry, a desmic system () is a set of three tetrahedra in 3-dimensional p ...
of three tetrahedra, where the third tetrahedron has as its four vertices the three crossing points at infinity and the centroid of the two finite tetrahedra. The same twelve tetrahedron vertices also form the points of Reye's configuration
In geometry, the Reye configuration, introduced by , is a configuration of 12 points and 16 lines.
Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye ...
.
The stella octangula numbers are figurate numbers that count the number of balls that can be arranged into the shape of a stellated octahedron. They are
:0, 1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990, ....
In popular culture
 The stellated octahedron appears with several other polyhedra and polyhedral compounds in M. C. Escher's print " Stars", and provides the central form in Escher's ''
The stellated octahedron appears with several other polyhedra and polyhedral compounds in M. C. Escher's print " Stars", and provides the central form in Escher's ''Double Planetoid
''Double Planetoid'' is a wood engraving print by the Dutch artist M. C. Escher, first printed in 1949.
Description
''Double Planetoid'' is printed in four colors from four wood blocks. It depicts a planetoid in the shape of a compound of two ...
'' (1949).
The obelisk in the center of the in Zaragoza
Zaragoza, also known in English as Saragossa,''Encyclopædia Britannica'"Zaragoza (conventional Saragossa)" is the capital city of the Zaragoza Province and of the autonomous community of Aragon, Spain. It lies by the Ebro river and its tribut ...
, Spain
, image_flag = Bandera de España.svg
, image_coat = Escudo de España (mazonado).svg
, national_motto = '' Plus ultra'' ( Latin)(English: "Further Beyond")
, national_anthem = (English: "Royal March")
, ...
, is surrounded by twelve stellated octahedral lamppposts, shaped to form a three-dimensional version of the Flag of Europe
The Flag of Europe or European Flag consists of twelve golden stars forming a circle on a blue field. It was designed and adopted in 1955 by the Council of Europe (CoE) as a symbol for the whole of Europe.
Since 1985, the flag has also b ...
.
Some modern mystics have associated this shape with the "merkaba", which according to them is a "counter-rotating energy field" named from an ancient Egyptian word. However, the word "merkaba" is actually Hebrew
Hebrew (; ; ) is a Northwest Semitic language of the Afroasiatic language family. Historically, it is one of the spoken languages of the Israelites and their longest-surviving descendants, the Jews and Samaritans. It was largely preserved ...
, and more properly refers to a chariot
A chariot is a type of cart driven by a charioteer, usually using horses to provide rapid motive power. The oldest known chariots have been found in burials of the Sintashta culture in modern-day Chelyabinsk Oblast, Russia, dated to c. 2000&nb ...
in the visions of Ezekiel
Ezekiel (; he, יְחֶזְקֵאל ''Yəḥezqēʾl'' ; in the Septuagint written in grc-koi, Ἰεζεκιήλ ) is the central protagonist of the Book of Ezekiel in the Hebrew Bible.
In Judaism, Christianity, and Islam, Ezekiel is ackn ...
.
The resemblance between this shape and the two-dimensional star of David
The Star of David (). is a generally recognized symbol of both Jewish identity and Judaism. Its shape is that of a hexagram: the compound of two equilateral triangles.
A derivation of the '' seal of Solomon'', which was used for decorat ...
has also been frequently noted.
References
External links
* *{{KlitzingPolytopes, ../incmats/so.htm, 3D compound, mode=cs2 Polyhedral stellation Polyhedral compounds