spacetime diagram on:
[Wikipedia]
[Google]
[Amazon]
 A spacetime diagram is a graphical illustration of the properties of space and time in the special theory of relativity. Spacetime diagrams allow a qualitative understanding of the corresponding phenomena like time dilation and
A spacetime diagram is a graphical illustration of the properties of space and time in the special theory of relativity. Spacetime diagrams allow a qualitative understanding of the corresponding phenomena like time dilation and
 In the study of 1-dimensional kinematics, position vs. time graphs (also called distance vs. time graphs, or p-t graphs) provide a useful means to describe motion. The specific features of the motion of objects are demonstrated by the shape and the slope of the lines. In Fig 1-1, the plotted object moves away from the origin at a uniform speed of 1.66 m/s for 6 seconds, halts for 5 seconds, then returns to the origin over a period of 7 seconds at a non-constant speed.
At its most basic level, a spacetime diagram is merely a time vs position graph, with the directions of the axes in a usual p-t graph exchanged, that is, the vertical axis refers to temporal and the horizontal axis to spatial coordinate values. Especially when used in special relativity (SR), the temporal axes of a spacetime diagram are scaled with the speed of light , and thus are often labeled by This changes the dimension of the addressed physical quantity from <''Time''> to <''Length''>, in accordance with the dimension associated with the spatial axes, which are frequently labeled
In the study of 1-dimensional kinematics, position vs. time graphs (also called distance vs. time graphs, or p-t graphs) provide a useful means to describe motion. The specific features of the motion of objects are demonstrated by the shape and the slope of the lines. In Fig 1-1, the plotted object moves away from the origin at a uniform speed of 1.66 m/s for 6 seconds, halts for 5 seconds, then returns to the origin over a period of 7 seconds at a non-constant speed.
At its most basic level, a spacetime diagram is merely a time vs position graph, with the directions of the axes in a usual p-t graph exchanged, that is, the vertical axis refers to temporal and the horizontal axis to spatial coordinate values. Especially when used in special relativity (SR), the temporal axes of a spacetime diagram are scaled with the speed of light , and thus are often labeled by This changes the dimension of the addressed physical quantity from <''Time''> to <''Length''>, in accordance with the dimension associated with the spatial axes, which are frequently labeled
 To ease insight into how spacetime coordinates, measured by observers in different
To ease insight into how spacetime coordinates, measured by observers in different
 The black axes labelled and on Fig 1-3 are the coordinate system of an observer, referred to as ''at rest'', and who is positioned at . This observer's world line is identical with the time axis. Each parallel line to this axis would correspond also to an object at rest but at another position. The blue line describes an object moving with constant speed to the right, such as a moving observer.
This blue line labelled may be interpreted as the time axis for the second observer. Together with the axis, which is identical for both observers, it represents their coordinate system. Since the reference frames are in standard configuration, both observers agree on the location of the origin of their coordinate systems. The axes for the moving observer are not perpendicular to each other and the scale on their time axis is stretched. To determine the coordinates of a certain event, two lines, each parallel to one of the two axes, must be constructed passing through the event, and their intersections with the axes read off.
Determining position and time of the event A as an example in the diagram leads to the same time for both observers, as expected. Only for the position different values result, because the moving observer has approached the position of the event A since . Generally stated, all events on a line parallel to the axis happen simultaneously for both observers. There is only one universal time , modelling the existence of one common position axis. On the other hand, due to two different time axes the observers usually measure different coordinates for the same event. This graphical translation from and to and and vice versa is described mathematically by the so-called
The black axes labelled and on Fig 1-3 are the coordinate system of an observer, referred to as ''at rest'', and who is positioned at . This observer's world line is identical with the time axis. Each parallel line to this axis would correspond also to an object at rest but at another position. The blue line describes an object moving with constant speed to the right, such as a moving observer.
This blue line labelled may be interpreted as the time axis for the second observer. Together with the axis, which is identical for both observers, it represents their coordinate system. Since the reference frames are in standard configuration, both observers agree on the location of the origin of their coordinate systems. The axes for the moving observer are not perpendicular to each other and the scale on their time axis is stretched. To determine the coordinates of a certain event, two lines, each parallel to one of the two axes, must be constructed passing through the event, and their intersections with the axes read off.
Determining position and time of the event A as an example in the diagram leads to the same time for both observers, as expected. Only for the position different values result, because the moving observer has approached the position of the event A since . Generally stated, all events on a line parallel to the axis happen simultaneously for both observers. There is only one universal time , modelling the existence of one common position axis. On the other hand, due to two different time axes the observers usually measure different coordinates for the same event. This graphical translation from and to and and vice versa is described mathematically by the so-called

 The term Minkowski diagram refers to a specific form of spacetime diagram frequently used in special relativity. A Minkowski diagram is a two-dimensional graphical depiction of a portion of Minkowski space, usually where space has been curtailed to a single dimension. The units of measurement in these diagrams are taken such that the light cone at an event consists of the lines of slope plus or minus one through that event. The horizontal lines correspond to the usual notion of ''simultaneous events'' for a stationary observer at the origin.
A particular Minkowski diagram illustrates the result of a Lorentz transformation. The Lorentz transformation relates two
The term Minkowski diagram refers to a specific form of spacetime diagram frequently used in special relativity. A Minkowski diagram is a two-dimensional graphical depiction of a portion of Minkowski space, usually where space has been curtailed to a single dimension. The units of measurement in these diagrams are taken such that the light cone at an event consists of the lines of slope plus or minus one through that event. The horizontal lines correspond to the usual notion of ''simultaneous events'' for a stationary observer at the origin.
A particular Minkowski diagram illustrates the result of a Lorentz transformation. The Lorentz transformation relates two
 The corresponding boost from and to and and vice versa is described mathematically by the Lorentz transformation, which can be written
:
where is the Lorentz factor. By applying the Lorentz transformation, the spacetime axes obtained for a boosted frame will always correspond to conjugate diameters of a pair of hyperbolas.
As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths. If is the unit length on the axes of and respectively, the unit length on the axes of and is:
:
The -axis represents the worldline of a clock resting in , with representing the duration between two events happening on this worldline, also called the proper time between these events. Length upon the -axis represents the rest length or proper length of a rod resting in . The same interpretation can also be applied to distance upon the - and -axes for clocks and rods resting in .
The corresponding boost from and to and and vice versa is described mathematically by the Lorentz transformation, which can be written
:
where is the Lorentz factor. By applying the Lorentz transformation, the spacetime axes obtained for a boosted frame will always correspond to conjugate diameters of a pair of hyperbolas.
As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths. If is the unit length on the axes of and respectively, the unit length on the axes of and is:
:
The -axis represents the worldline of a clock resting in , with representing the duration between two events happening on this worldline, also called the proper time between these events. Length upon the -axis represents the rest length or proper length of a rod resting in . The same interpretation can also be applied to distance upon the - and -axes for clocks and rods resting in .
 Relativistic time dilation refers to the fact that a clock (indicating its proper time in its rest frame) that moves relative to an observer is observed to run slower. The situation is depicted in the symmetric Loedel diagrams of Fig 4-1. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-2, the observer whose reference frame is given by the black axes is assumed to move from the origin O towards A. The moving clock has the reference frame given by the blue axes and moves from O to B. For the black observer, all events happening simultaneously with the event at A are located on a straight line parallel to its space axis. This line passes through A and B, so A and B are simultaneous from the reference frame of the observer with black axes. However, the clock that is moving relative to the black observer marks off time along the blue time axis. This is represented by the distance from O to B. Therefore, the observer at A with the black axes notices their clock as reading the distance from O to A while they observe the clock moving relative him or her to read the distance from O to B. Due to the distance from O to B being smaller than the distance from O to A, they conclude that the time passed on the clock moving relative to them is smaller than that passed on their own clock.
A second observer, having moved together with the clock from O to B, will argue that the black axis clock has only reached C and therefore runs slower. The reason for these apparently paradoxical statements is the different determination of the events happening synchronously at different locations. Due to the principle of relativity, the question of who is right has no answer and does not make sense.
Relativistic time dilation refers to the fact that a clock (indicating its proper time in its rest frame) that moves relative to an observer is observed to run slower. The situation is depicted in the symmetric Loedel diagrams of Fig 4-1. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-2, the observer whose reference frame is given by the black axes is assumed to move from the origin O towards A. The moving clock has the reference frame given by the blue axes and moves from O to B. For the black observer, all events happening simultaneously with the event at A are located on a straight line parallel to its space axis. This line passes through A and B, so A and B are simultaneous from the reference frame of the observer with black axes. However, the clock that is moving relative to the black observer marks off time along the blue time axis. This is represented by the distance from O to B. Therefore, the observer at A with the black axes notices their clock as reading the distance from O to A while they observe the clock moving relative him or her to read the distance from O to B. Due to the distance from O to B being smaller than the distance from O to A, they conclude that the time passed on the clock moving relative to them is smaller than that passed on their own clock.
A second observer, having moved together with the clock from O to B, will argue that the black axis clock has only reached C and therefore runs slower. The reason for these apparently paradoxical statements is the different determination of the events happening synchronously at different locations. Due to the principle of relativity, the question of who is right has no answer and does not make sense.
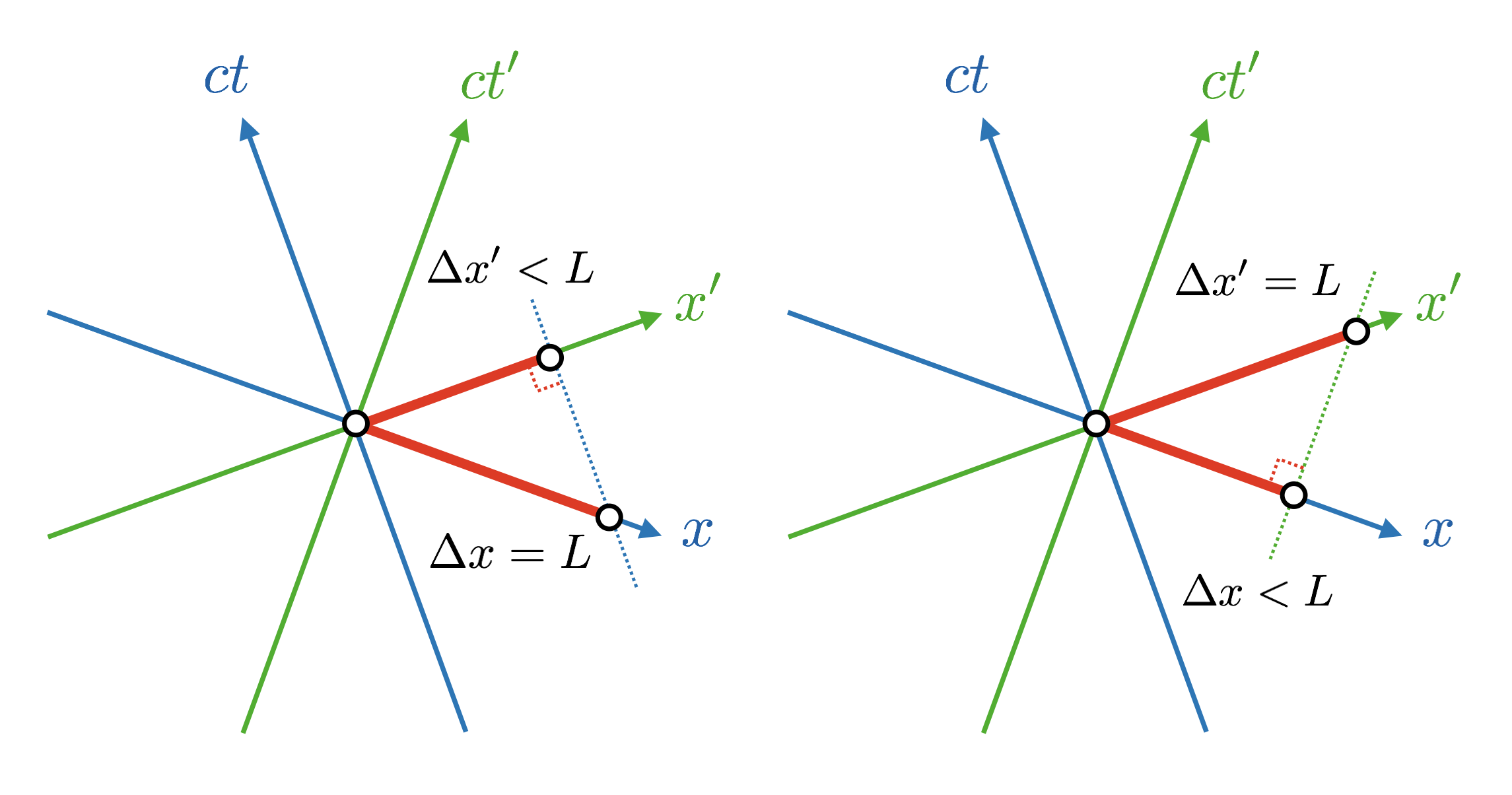 Relativistic length contraction refers to the fact that a ruler (indicating its proper length in its rest frame) that moves relative to an observer is observed to contract/shorten. The situation is depicted in symmetric Loedel diagrams in Fig 4-3. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-4, the observer is assumed again to move along the -axis. The world lines of the endpoints of an object moving relative to him are assumed to move along the -axis and the parallel line passing through A and B. For this observer the endpoints of the object at are O and A. For a second observer moving together with the object, so that for him the object is at rest, it has the proper length OB at . Due to . the object is contracted for the first observer.
The second observer will argue that the first observer has evaluated the endpoints of the object at O and A respectively and therefore at different times, leading to a wrong result due to his motion in the meantime. If the second observer investigates the length of another object with endpoints moving along the -axis and a parallel line passing through C and D he concludes the same way this object to be contracted from OD to OC. Each observer estimates objects moving with the other observer to be contracted. This apparently paradoxical situation is again a consequence of the relativity of simultaneity as demonstrated by the analysis via Minkowski diagram.
For all these considerations it was assumed, that both observers take into account the speed of light and their distance to all events they see in order to determine the actual times at which these events happen from their point of view.
Relativistic length contraction refers to the fact that a ruler (indicating its proper length in its rest frame) that moves relative to an observer is observed to contract/shorten. The situation is depicted in symmetric Loedel diagrams in Fig 4-3. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-4, the observer is assumed again to move along the -axis. The world lines of the endpoints of an object moving relative to him are assumed to move along the -axis and the parallel line passing through A and B. For this observer the endpoints of the object at are O and A. For a second observer moving together with the object, so that for him the object is at rest, it has the proper length OB at . Due to . the object is contracted for the first observer.
The second observer will argue that the first observer has evaluated the endpoints of the object at O and A respectively and therefore at different times, leading to a wrong result due to his motion in the meantime. If the second observer investigates the length of another object with endpoints moving along the -axis and a parallel line passing through C and D he concludes the same way this object to be contracted from OD to OC. Each observer estimates objects moving with the other observer to be contracted. This apparently paradoxical situation is again a consequence of the relativity of simultaneity as demonstrated by the analysis via Minkowski diagram.
For all these considerations it was assumed, that both observers take into account the speed of light and their distance to all events they see in order to determine the actual times at which these events happen from their point of view.
 Another postulate of special relativity is the constancy of the speed of light. It says that any observer in an inertial reference frame measuring the vacuum speed of light relative to themself obtains the same value regardless of his own motion and that of the light source. This statement seems to be paradoxical, but it follows immediately from the differential equation yielding this, and the Minkowski diagram agrees. It explains also the result of the Michelson–Morley experiment which was considered to be a mystery before the theory of relativity was discovered, when photons were thought to be waves through an undetectable medium.
For world lines of photons passing the origin in different directions and holds. That means any position on such a world line corresponds with steps on - and -axes of equal absolute value. From the rule for reading off coordinates in coordinate system with tilted axes follows that the two world lines are the angle bisectors of the - and -axes. As shown in Fig 4-5, the Minkowski diagram illustrates them as being angle bisectors of the - and -axes as well. That means both observers measure the same speed for both photons.
Further coordinate systems corresponding to observers with arbitrary velocities can be added to this Minkowski diagram. For all these systems both photon world lines represent the angle bisectors of the axes. The more the relative speed approaches the speed of light the more the axes approach the corresponding angle bisector. The axis is always more flat and the time axis more steep than the photon world lines. The scales on both axes are always identical, but usually different from those of the other coordinate systems.
Another postulate of special relativity is the constancy of the speed of light. It says that any observer in an inertial reference frame measuring the vacuum speed of light relative to themself obtains the same value regardless of his own motion and that of the light source. This statement seems to be paradoxical, but it follows immediately from the differential equation yielding this, and the Minkowski diagram agrees. It explains also the result of the Michelson–Morley experiment which was considered to be a mystery before the theory of relativity was discovered, when photons were thought to be waves through an undetectable medium.
For world lines of photons passing the origin in different directions and holds. That means any position on such a world line corresponds with steps on - and -axes of equal absolute value. From the rule for reading off coordinates in coordinate system with tilted axes follows that the two world lines are the angle bisectors of the - and -axes. As shown in Fig 4-5, the Minkowski diagram illustrates them as being angle bisectors of the - and -axes as well. That means both observers measure the same speed for both photons.
Further coordinate systems corresponding to observers with arbitrary velocities can be added to this Minkowski diagram. For all these systems both photon world lines represent the angle bisectors of the axes. The more the relative speed approaches the speed of light the more the axes approach the corresponding angle bisector. The axis is always more flat and the time axis more steep than the photon world lines. The scales on both axes are always identical, but usually different from those of the other coordinate systems.
 Straight lines passing the origin which are steeper than both photon world lines correspond with objects moving more slowly than the speed of light. If this applies to an object, then it applies from the viewpoint of all observers, because the world lines of these photons are the angle bisectors for any inertial reference frame. Therefore, any point above the origin and between the world lines of both photons can be reached with a speed smaller than that of the light and can have a cause-and-effect relationship with the origin. This area is the absolute future, because any event there happens later compared to the event represented by the origin regardless of the observer, which is obvious graphically from the Minkowski diagram in Fig 4-6.
Following the same argument the range below the origin and between the photon world lines is the absolute past relative to the origin. Any event there belongs definitely to the past and can be the cause of an effect at the origin.
The relationship between any such pairs of event is called ''timelike'', because they have a time distance greater than zero for all observers. A straight line connecting these two events is always the time axis of a possible observer for whom they happen at the same place. Two events which can be connected just with the speed of light are called ''lightlike''.
In principle a further dimension of space can be added to the Minkowski diagram leading to a three-dimensional representation. In this case the ranges of future and past become cones with apexes touching each other at the origin. They are called
Straight lines passing the origin which are steeper than both photon world lines correspond with objects moving more slowly than the speed of light. If this applies to an object, then it applies from the viewpoint of all observers, because the world lines of these photons are the angle bisectors for any inertial reference frame. Therefore, any point above the origin and between the world lines of both photons can be reached with a speed smaller than that of the light and can have a cause-and-effect relationship with the origin. This area is the absolute future, because any event there happens later compared to the event represented by the origin regardless of the observer, which is obvious graphically from the Minkowski diagram in Fig 4-6.
Following the same argument the range below the origin and between the photon world lines is the absolute past relative to the origin. Any event there belongs definitely to the past and can be the cause of an effect at the origin.
The relationship between any such pairs of event is called ''timelike'', because they have a time distance greater than zero for all observers. A straight line connecting these two events is always the time axis of a possible observer for whom they happen at the same place. Two events which can be connected just with the speed of light are called ''lightlike''.
In principle a further dimension of space can be added to the Minkowski diagram leading to a three-dimensional representation. In this case the ranges of future and past become cones with apexes touching each other at the origin. They are called
 Following the same argument, all straight lines passing through the origin and which are more nearly horizontal than the photon world lines, would correspond to objects or signals moving faster than light regardless of the speed of the observer. Therefore, no event outside the light cones can be reached from the origin, even by a light-signal, nor by any object or signal moving with less than the speed of light. Such pairs of events are called ''spacelike'' because they have a finite spatial distance different from zero for all observers. On the other hand, a straight line connecting such events is always the space coordinate axis of a possible observer for whom they happen at the same time. By a slight variation of the velocity of this coordinate system in both directions it is always possible to find two inertial reference frames whose observers estimate the chronological order of these events to be different.
Given an object moving faster than light, say from O to A in Fig 4-7, then for any observer watching the object moving from O to A, another observer can be found (moving at less than the speed of light with respect to the first) for whom the object moves from A to O. The question of which observer is right has no unique answer, and therefore makes no physical sense. Any such moving object or signal would violate the principle of causality.
Also, any general technical means of sending signals faster than light would permit information to be sent into the originator's own past. In the diagram, an observer at O in the system sends a message moving faster than light to A. At A, it is received by another observer, moving so as to be in the system, who sends it back, again faster than light, arriving at B. But B is in the past relative to O. The absurdity of this process becomes obvious when both observers subsequently confirm that they received no message at all, but all messages were directed towards the other observer as can be seen graphically in the Minkowski diagram. Furthermore, if it were possible to accelerate an observer to the speed of light, their space and time axes would coincide with their angle bisector. The coordinate system would collapse, in concordance with the fact that due to time dilation, time would effectively stop passing for them.
These considerations show that the speed of light as a limit is a consequence of the properties of spacetime, and not of the properties of objects such as technologically imperfect space ships. The prohibition of faster-than-light motion, therefore, has nothing in particular to do with electromagnetic waves or light, but comes as a consequence of the structure of spacetime.
Following the same argument, all straight lines passing through the origin and which are more nearly horizontal than the photon world lines, would correspond to objects or signals moving faster than light regardless of the speed of the observer. Therefore, no event outside the light cones can be reached from the origin, even by a light-signal, nor by any object or signal moving with less than the speed of light. Such pairs of events are called ''spacelike'' because they have a finite spatial distance different from zero for all observers. On the other hand, a straight line connecting such events is always the space coordinate axis of a possible observer for whom they happen at the same time. By a slight variation of the velocity of this coordinate system in both directions it is always possible to find two inertial reference frames whose observers estimate the chronological order of these events to be different.
Given an object moving faster than light, say from O to A in Fig 4-7, then for any observer watching the object moving from O to A, another observer can be found (moving at less than the speed of light with respect to the first) for whom the object moves from A to O. The question of which observer is right has no unique answer, and therefore makes no physical sense. Any such moving object or signal would violate the principle of causality.
Also, any general technical means of sending signals faster than light would permit information to be sent into the originator's own past. In the diagram, an observer at O in the system sends a message moving faster than light to A. At A, it is received by another observer, moving so as to be in the system, who sends it back, again faster than light, arriving at B. But B is in the past relative to O. The absurdity of this process becomes obvious when both observers subsequently confirm that they received no message at all, but all messages were directed towards the other observer as can be seen graphically in the Minkowski diagram. Furthermore, if it were possible to accelerate an observer to the speed of light, their space and time axes would coincide with their angle bisector. The coordinate system would collapse, in concordance with the fact that due to time dilation, time would effectively stop passing for them.
These considerations show that the speed of light as a limit is a consequence of the properties of spacetime, and not of the properties of objects such as technologically imperfect space ships. The prohibition of faster-than-light motion, therefore, has nothing in particular to do with electromagnetic waves or light, but comes as a consequence of the structure of spacetime.
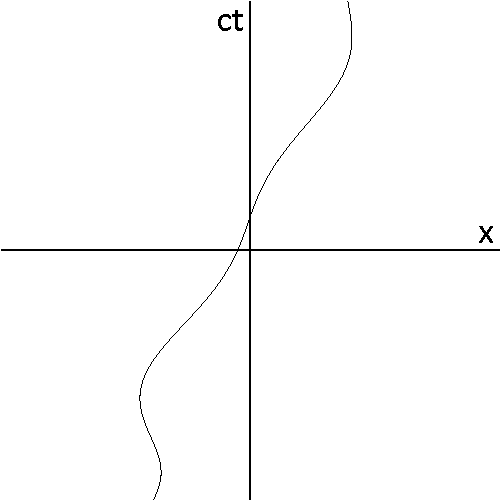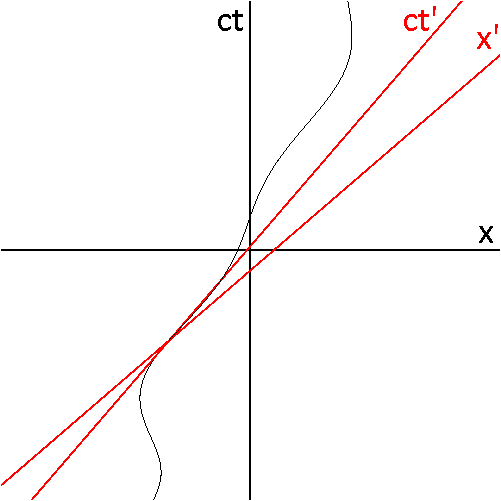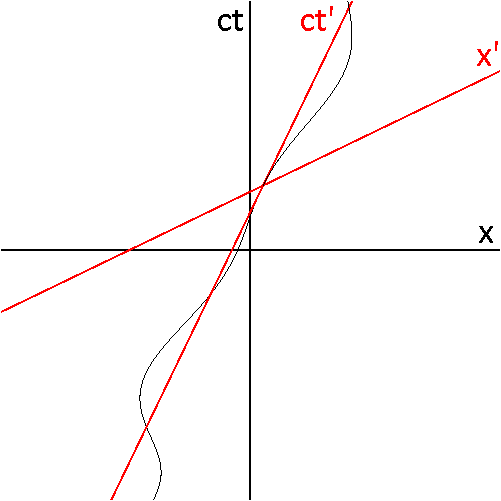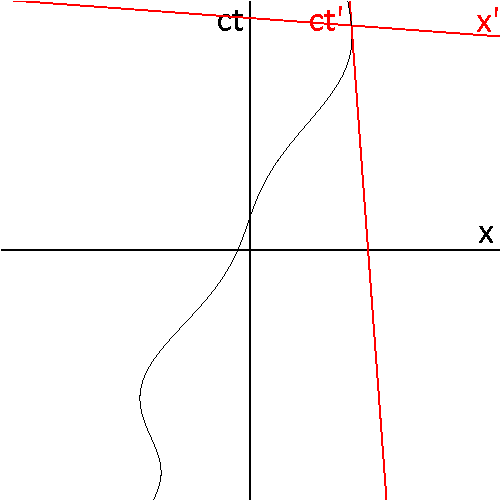
 It is often, incorrectly, asserted that special relativity cannot handle accelerating particles or accelerating reference frames. In reality, accelerating particles present no difficulty at all in special relativity. On the other hand, accelerating ''frames'' do require some special treatment, However, as long as one is dealing with flat, Minkowskian spacetime, special relativity can handle the situation. It is only in the presence of gravitation that general relativity is required.
An accelerating particle's 4-vector acceleration is the derivative with respect to proper time of its 4-velocity. This is not a difficult situation to handle. Accelerating frames require that one understand the concept of a ''momentarily comoving reference frame'' (MCRF), which is to say, a frame traveling at the same instantaneous velocity of a particle at any given instant.
Consider the animation in Fig 5-1. The curved line represents the world line of a particle that undergoes continuous acceleration, including complete changes of direction in the positive and negative x-directions. The red axes are the axes of the MCRF for each point along the particle's trajectory. The coordinates of events in the unprimed (stationary) frame can be related to their coordinates in any momentarily co-moving primed frame using the Lorentz transformations.
Fig 5-2 illustrates the changing views of spacetime along the world line of a rapidly accelerating particle. The axis (not drawn) is vertical, while the axis (not drawn) is horizontal. The dashed line is the spacetime trajectory ("world line") of the particle. The balls are placed at regular intervals of proper time along the world line. The solid diagonal lines are the light cones for the observer's current event, and they intersect at that event. The small dots are other arbitrary events in the spacetime.
The slope of the world line (deviation from being vertical) is the velocity of the particle on that section of the world line. Bends in the world line represent particle acceleration. As the particle accelerates, its view of spacetime changes. These changes in view are governed by the Lorentz transformations. Also note that:
* the balls on the world line before/after future/past accelerations are more spaced out due to time dilation.
* events which were simultaneous before an acceleration (horizontally spaced events) are at different times afterwards due to the relativity of simultaneity,
* events pass through the light cone lines due to the progression of proper time, but not due to the change of views caused by the accelerations, and
* the world line always remains within the future and past light cones of the current event.
If one imagines each event to be the flashing of a light, then the events that are within the past light cone of the observer are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the velocity relative to the observer.
It is often, incorrectly, asserted that special relativity cannot handle accelerating particles or accelerating reference frames. In reality, accelerating particles present no difficulty at all in special relativity. On the other hand, accelerating ''frames'' do require some special treatment, However, as long as one is dealing with flat, Minkowskian spacetime, special relativity can handle the situation. It is only in the presence of gravitation that general relativity is required.
An accelerating particle's 4-vector acceleration is the derivative with respect to proper time of its 4-velocity. This is not a difficult situation to handle. Accelerating frames require that one understand the concept of a ''momentarily comoving reference frame'' (MCRF), which is to say, a frame traveling at the same instantaneous velocity of a particle at any given instant.
Consider the animation in Fig 5-1. The curved line represents the world line of a particle that undergoes continuous acceleration, including complete changes of direction in the positive and negative x-directions. The red axes are the axes of the MCRF for each point along the particle's trajectory. The coordinates of events in the unprimed (stationary) frame can be related to their coordinates in any momentarily co-moving primed frame using the Lorentz transformations.
Fig 5-2 illustrates the changing views of spacetime along the world line of a rapidly accelerating particle. The axis (not drawn) is vertical, while the axis (not drawn) is horizontal. The dashed line is the spacetime trajectory ("world line") of the particle. The balls are placed at regular intervals of proper time along the world line. The solid diagonal lines are the light cones for the observer's current event, and they intersect at that event. The small dots are other arbitrary events in the spacetime.
The slope of the world line (deviation from being vertical) is the velocity of the particle on that section of the world line. Bends in the world line represent particle acceleration. As the particle accelerates, its view of spacetime changes. These changes in view are governed by the Lorentz transformations. Also note that:
* the balls on the world line before/after future/past accelerations are more spaced out due to time dilation.
* events which were simultaneous before an acceleration (horizontally spaced events) are at different times afterwards due to the relativity of simultaneity,
* events pass through the light cone lines due to the progression of proper time, but not due to the change of views caused by the accelerations, and
* the world line always remains within the future and past light cones of the current event.
If one imagines each event to be the flashing of a light, then the events that are within the past light cone of the observer are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the velocity relative to the observer.

 The photon world lines are determined using the metric with . The
The photon world lines are determined using the metric with . The
length contraction
Length contraction is the phenomenon that a moving object's length is measured to be shorter than its proper length, which is the length as measured in the object's own rest frame. It is also known as Lorentz contraction or Lorentz–FitzGerald ...
without mathematical equations.
The history of an object's location throughout all time traces out a line, referred to as the object's world line, in a spacetime diagram. Points in spacetime diagrams represent a fixed position in space and time and are referred to as events.
The most well-known class of spacetime diagrams are known as Minkowski diagrams, developed by Hermann Minkowski
Hermann Minkowski (; ; 22 June 1864 – 12 January 1909) was a German mathematician and professor at Königsberg, Zürich and Göttingen. He created and developed the geometry of numbers and used geometrical methods to solve problems in number t ...
in 1908. Minkowski diagrams are two-dimensional graphs that depict events as happening in a universe consisting of one space dimension and one time dimension. Unlike a regular distance-time graph, the distance is displayed on the horizontal axis and time on the vertical axis. Additionally, the time and space units of measurement are chosen in such a way that an object moving at the speed of light is depicted as following a 45° angle to the diagram's axes.
Introduction to kinetic diagrams
Position versus time graphs
Standard configuration of reference frames
reference frames
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathema ...
, compare with each other, it is useful to work with a simplified setup. With care, this allows simplification of the math with no loss of generality in the conclusions that are reached. Setting the temporal component aside for the moment, two Galilean reference frame
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. ...
s (i.e. conventional 3-space frames), S and S′ (pronounced "S prime"), each with observers O and O′ at rest in their respective frames, but measuring the other as moving with speeds ±''v'' are said to be in ''standard configuration'', when:
* The ''x'', ''y'', ''z'' axes of frame S are oriented parallel to the respective primed axes of frame S′.
* Frame S′ moves in the ''x''-direction of frame S with a constant velocity ''v'' as measured in frame S.
* The origins of frames S and S′ coincide for time ''t'' = 0 in frame S and ''t''′ = 0 in frame S′.
This spatial setting is displayed in the Fig 1-2, in which the temporal coordinates are separately annotated as quantities ''t'' and ''t.
In a further step of simplification it is often possible to consider just the direction of the observed motion and ignore the other two spatial components, allowing ''x'' and ''ct'' to be plotted in 2-dimensional spacetime diagrams, as introduced above.
Non-relativistic "spacetime diagrams"
Galilean transformation
In physics, a Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. These transformations together with spatial rotatio ...
.
Minkowski diagrams
Overview
 The term Minkowski diagram refers to a specific form of spacetime diagram frequently used in special relativity. A Minkowski diagram is a two-dimensional graphical depiction of a portion of Minkowski space, usually where space has been curtailed to a single dimension. The units of measurement in these diagrams are taken such that the light cone at an event consists of the lines of slope plus or minus one through that event. The horizontal lines correspond to the usual notion of ''simultaneous events'' for a stationary observer at the origin.
A particular Minkowski diagram illustrates the result of a Lorentz transformation. The Lorentz transformation relates two
The term Minkowski diagram refers to a specific form of spacetime diagram frequently used in special relativity. A Minkowski diagram is a two-dimensional graphical depiction of a portion of Minkowski space, usually where space has been curtailed to a single dimension. The units of measurement in these diagrams are taken such that the light cone at an event consists of the lines of slope plus or minus one through that event. The horizontal lines correspond to the usual notion of ''simultaneous events'' for a stationary observer at the origin.
A particular Minkowski diagram illustrates the result of a Lorentz transformation. The Lorentz transformation relates two inertial frames of reference
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration ...
, where an observer stationary at the event makes a change of velocity along the -axis. As shown in Fig 2-1, the new time axis of the observer forms an angle with the previous time axis, with . In the new frame of reference the simultaneous events lie parallel to a line inclined by to the previous lines of simultaneity. This is the new -axis. Both the original set of axes and the primed set of axes have the property that they are orthogonal with respect to the Minkowski inner product
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inert ...
or ''relativistic dot product''.
Whatever the magnitude of , the line forms the universal bisector, as shown in Fig 2-2.
One frequently encounters Minkowski diagrams where the time units of measurement are scaled by a factor of such that one unit of equals one unit of . Such a diagram may have units of
* Approximately 30 centimetres length and nanoseconds
* Astronomical units and intervals of about 8 minutes and 19 seconds (499 seconds)
* Light year
A light-year, alternatively spelled light year, is a large unit of length used to express astronomical distances and is equivalent to about 9.46 trillion kilometers (), or 5.88 trillion miles ().One trillion here is taken to be 1012 ...
s and years
* Light-second and second
With that, light paths are represented by lines parallel to the bisector between the axes.
Mathematical details
The angle between the and axes will be identical with that between the time axes and . This follows from the second postulate of special relativity, which says that the speed of light is the same for all observers, regardless of their relative motion (see below). The angle is given by :History
Albert Einstein discovered special relativity in 1905, withHermann Minkowski
Hermann Minkowski (; ; 22 June 1864 – 12 January 1909) was a German mathematician and professor at Königsberg, Zürich and Göttingen. He created and developed the geometry of numbers and used geometrical methods to solve problems in number t ...
providing his graphical representation in 1908.
: Various English translations on Wikisource: Space and Time
In Minkowski's 1908 paper there were three diagrams, first to illustrate the Lorentz transformation, then the partition of the plane by the light-cone, and finally illustration of worldlines. The first diagram used a branch of the unit hyperbola to show the locus of a unit of proper time depending on velocity, thus illustrating time dilation. The second diagram showed the conjugate hyperbola to calibrate space, where a similar stretching leaves the impression of FitzGerald contraction
Length contraction is the phenomenon that a moving object's length is measured to be shorter than its proper length, which is the length as measured in the object's own rest frame. It is also known as Lorentz contraction or Lorentz–FitzGerald ...
. In 1914 Ludwik Silberstein included a diagram of "Minkowski's representation of the Lorentz transformation". This diagram included the unit hyperbola, its conjugate, and a pair of conjugate diameters. Since the 1960s a version of this more complete configuration has been referred to as The Minkowski Diagram, and used as a standard illustration of the transformation geometry of special relativity. E. T. Whittaker has pointed out that the principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference.
For example, in the framework of special relativity the Maxwell equations have ...
is tantamount to the arbitrariness of what hyperbola radius is selected for time in the Minkowski diagram. In 1912 Gilbert N. Lewis
Gilbert Newton Lewis (October 23 or October 25, 1875 – March 23, 1946) was an American physical chemist and a Dean of the College of Chemistry at University of California, Berkeley. Lewis was best known for his discovery of the covalent bond a ...
and Edwin B. Wilson
Edwin Bidwell Wilson (April 25, 1879 – December 28, 1964) was an American mathematician, statistician, physicist and general polymath. He was the sole protégé of Yale University physicist Josiah Willard Gibbs and was mentor to MIT economist ...
applied the methods of synthetic geometry to develop the properties of the non-Euclidean
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geo ...
plane that has Minkowski diagrams.
When Taylor and Wheeler composed ''Spacetime Physics'' (1966), they did ''not'' use the term ''Minkowski diagram'' for their spacetime geometry. Instead they included an acknowledgement of Minkowski's contribution to philosophy by the totality of his innovation of 1908.
Loedel diagrams
While a frame at rest in a Minkowski diagram has orthogonal spacetime axes, a frame moving relative to the rest frame in a Minkowski diagram has spacetime axes which form an acute angle. This asymmetry of Minkowski diagrams can be misleading, since special relativity postulates that any twoinertial reference frames
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. ...
must be physically equivalent. The Loedel diagram is an alternative spacetime diagram that makes the symmetry of inertial references frames much more manifest.
Formulation via median frame
Several authors showed that there is a frame of reference between the resting and moving ones where their symmetry would be apparent ("median frame"). In this frame, the two other frames are moving in opposite directions with equal speed. Using such coordinates makes the units of length and time the same for both axes. If and are given between and , then these expressions are connected with the values in their median frame ''S''0 as follows: (Translation: The Lorentz–Einstein transformation and the universal time of Ed. Guillaume) : For instance, if between and , then by (2) they are moving in their median frame ''S''0 with approximately each in opposite directions. On the other hand, if in ''S''0, then by (1) the relative velocity between and in their own rest frames is . The construction of the axes of and is done in accordance with the ordinary method using with respect to the orthogonal axes of the median frame (Fig. 3-1). However, it turns out that when drawing such a symmetric diagram, it is possible to derive the diagram's relations even without mentioning the median frame and at all. Instead, the relative velocity between and can directly be used in the following construction, providing the same result: If is the angle between the axes of and (or between and ), and between the axes of and , it is given: : Two methods of construction are obvious from Fig. 3-2: the -axis is drawn perpendicular to the -axis, the and -axes are added at angle ; and the ''x''′-axis is drawn at angle with respect to the -axis, the -axis is added perpendicular to the -axis and the -axis perpendicular to the -axis. In a Minkowski diagram, lengths on the page cannot be directly compared to each other, due to warping factor between the axes' unit lengths in a Minkowski diagram. In particular, if and are the unit lengths of the rest frame axes and moving frame axes, respectively, in a Minkowski diagram, then the two unit lengths are warped relative to each other via the formula: : By contrast, in a symmetric Loedel diagram, both the and frame axes are warped by the same factor relative to the median frame and hence have identical unit lengths. This implies that, for a Loedel spacetime diagram, we can directly compare spacetime lengths between different frames as they appear on the page; no unit length scaling/conversion between frames is necessary due to the symmetric nature of the Loedel diagram.History
*Max Born
Max Born (; 11 December 1882 – 5 January 1970) was a German physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a n ...
(1920) drew Minkowski diagrams by placing the -axis almost perpendicular to the -axis, as well as the -axis to the -axis, in order to demonstrate length contraction and time dilation in the symmetric case of two rods and two clocks moving in opposite direction.
* Dmitry Mirimanoff (1921) showed that there is always a median frame with respect to two relatively moving frames, and derived the relations between them from the Lorentz transformation. However, he didn't give a graphical representation in a diagram.
* Symmetric diagrams were systematically developed by Paul Gruner
Paul may refer to:
*Paul (given name), a given name (includes a list of people with that name)
*Paul (surname), a list of people
People
Christianity
* Paul the Apostle (AD c.5–c.64/65), also known as Saul of Tarsus or Saint Paul, early Chri ...
in collaboration with Josef Sauter in two papers in 1921. Relativistic effects such as length contraction and time dilation and some relations to covariant and contravariant vectors were demonstrated by them. (Translation: Elementary geometric representation of the formulas of the special theory of relativity) (translation: An elementary geometrical representation of the transformation formulas of the special theory of relativity) Gruner extended this method in subsequent papers (1922–1924), and gave credit to Mirimanoff's treatment as well. (translation: Graphical representation of the four-dimensional space-time universe)
* The construction of symmetric Minkowski diagrams was later independently rediscovered by several authors. For instance, starting in 1948, Enrique Loedel Palumbo
Enrique Loedel Palumbo (Montevideo Uruguay, June 29, 1901 – La Plata Argentina, July 31, 1962) was an Uruguayan physicist.
Loedel Palumbo was born in Montevideo, Uruguay and studied at the University of La Plata in Argentina. His doctoral advis ...
published a series of papers in Spanish language, presenting the details of such an approach. In 1955, Henri Amar
Henri is an Estonian, Finnish, French, German and Luxembourgish form of the masculine given name Henry (given name), Henry.
People with this given name
; French noblemen
:'' See the 'List_of_rulers_named_Henry#France, List of rulers named Henry ...
also published a paper presenting such relations, and gave credit to Loedel in a subsequent paper in 1957. Some authors of textbooks use symmetric Minkowski diagrams, denoting as ''Loedel diagrams''.
Relativistic phenomena in diagrams
Time dilation
 Relativistic time dilation refers to the fact that a clock (indicating its proper time in its rest frame) that moves relative to an observer is observed to run slower. The situation is depicted in the symmetric Loedel diagrams of Fig 4-1. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-2, the observer whose reference frame is given by the black axes is assumed to move from the origin O towards A. The moving clock has the reference frame given by the blue axes and moves from O to B. For the black observer, all events happening simultaneously with the event at A are located on a straight line parallel to its space axis. This line passes through A and B, so A and B are simultaneous from the reference frame of the observer with black axes. However, the clock that is moving relative to the black observer marks off time along the blue time axis. This is represented by the distance from O to B. Therefore, the observer at A with the black axes notices their clock as reading the distance from O to A while they observe the clock moving relative him or her to read the distance from O to B. Due to the distance from O to B being smaller than the distance from O to A, they conclude that the time passed on the clock moving relative to them is smaller than that passed on their own clock.
A second observer, having moved together with the clock from O to B, will argue that the black axis clock has only reached C and therefore runs slower. The reason for these apparently paradoxical statements is the different determination of the events happening synchronously at different locations. Due to the principle of relativity, the question of who is right has no answer and does not make sense.
Relativistic time dilation refers to the fact that a clock (indicating its proper time in its rest frame) that moves relative to an observer is observed to run slower. The situation is depicted in the symmetric Loedel diagrams of Fig 4-1. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-2, the observer whose reference frame is given by the black axes is assumed to move from the origin O towards A. The moving clock has the reference frame given by the blue axes and moves from O to B. For the black observer, all events happening simultaneously with the event at A are located on a straight line parallel to its space axis. This line passes through A and B, so A and B are simultaneous from the reference frame of the observer with black axes. However, the clock that is moving relative to the black observer marks off time along the blue time axis. This is represented by the distance from O to B. Therefore, the observer at A with the black axes notices their clock as reading the distance from O to A while they observe the clock moving relative him or her to read the distance from O to B. Due to the distance from O to B being smaller than the distance from O to A, they conclude that the time passed on the clock moving relative to them is smaller than that passed on their own clock.
A second observer, having moved together with the clock from O to B, will argue that the black axis clock has only reached C and therefore runs slower. The reason for these apparently paradoxical statements is the different determination of the events happening synchronously at different locations. Due to the principle of relativity, the question of who is right has no answer and does not make sense.
Length contraction
 Relativistic length contraction refers to the fact that a ruler (indicating its proper length in its rest frame) that moves relative to an observer is observed to contract/shorten. The situation is depicted in symmetric Loedel diagrams in Fig 4-3. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-4, the observer is assumed again to move along the -axis. The world lines of the endpoints of an object moving relative to him are assumed to move along the -axis and the parallel line passing through A and B. For this observer the endpoints of the object at are O and A. For a second observer moving together with the object, so that for him the object is at rest, it has the proper length OB at . Due to . the object is contracted for the first observer.
The second observer will argue that the first observer has evaluated the endpoints of the object at O and A respectively and therefore at different times, leading to a wrong result due to his motion in the meantime. If the second observer investigates the length of another object with endpoints moving along the -axis and a parallel line passing through C and D he concludes the same way this object to be contracted from OD to OC. Each observer estimates objects moving with the other observer to be contracted. This apparently paradoxical situation is again a consequence of the relativity of simultaneity as demonstrated by the analysis via Minkowski diagram.
For all these considerations it was assumed, that both observers take into account the speed of light and their distance to all events they see in order to determine the actual times at which these events happen from their point of view.
Relativistic length contraction refers to the fact that a ruler (indicating its proper length in its rest frame) that moves relative to an observer is observed to contract/shorten. The situation is depicted in symmetric Loedel diagrams in Fig 4-3. Note that we can compare spacetime lengths on page directly with each other, due to the symmetric nature of the Loedel diagram.
In Fig 4-4, the observer is assumed again to move along the -axis. The world lines of the endpoints of an object moving relative to him are assumed to move along the -axis and the parallel line passing through A and B. For this observer the endpoints of the object at are O and A. For a second observer moving together with the object, so that for him the object is at rest, it has the proper length OB at . Due to . the object is contracted for the first observer.
The second observer will argue that the first observer has evaluated the endpoints of the object at O and A respectively and therefore at different times, leading to a wrong result due to his motion in the meantime. If the second observer investigates the length of another object with endpoints moving along the -axis and a parallel line passing through C and D he concludes the same way this object to be contracted from OD to OC. Each observer estimates objects moving with the other observer to be contracted. This apparently paradoxical situation is again a consequence of the relativity of simultaneity as demonstrated by the analysis via Minkowski diagram.
For all these considerations it was assumed, that both observers take into account the speed of light and their distance to all events they see in order to determine the actual times at which these events happen from their point of view.
Constancy of the speed of light
Speed of light and causality
light cones
In special and general relativity, a light cone (or "null cone") is the path that a flash of light, emanating from a single event (localized to a single point in space and a single moment in time) and traveling in all directions, would take thro ...
.
The speed of light as a limit
Accelerating observers
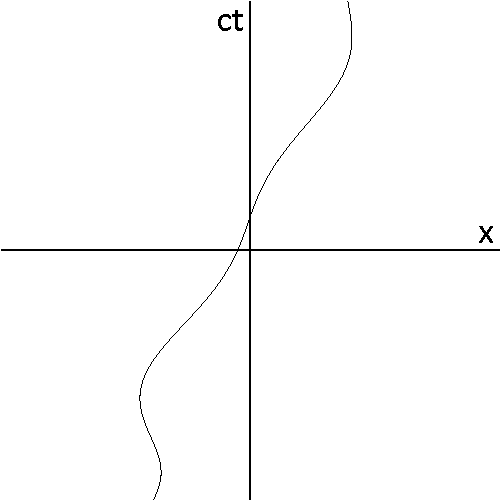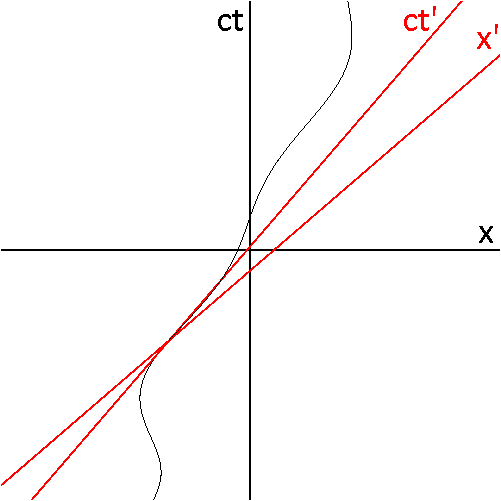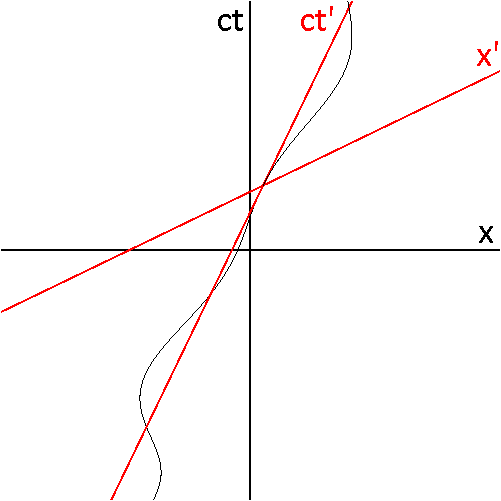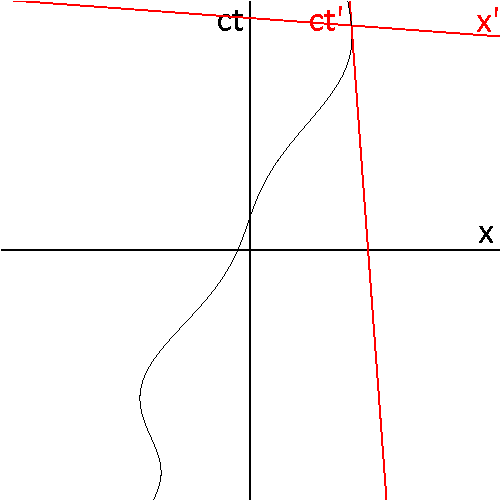
 It is often, incorrectly, asserted that special relativity cannot handle accelerating particles or accelerating reference frames. In reality, accelerating particles present no difficulty at all in special relativity. On the other hand, accelerating ''frames'' do require some special treatment, However, as long as one is dealing with flat, Minkowskian spacetime, special relativity can handle the situation. It is only in the presence of gravitation that general relativity is required.
An accelerating particle's 4-vector acceleration is the derivative with respect to proper time of its 4-velocity. This is not a difficult situation to handle. Accelerating frames require that one understand the concept of a ''momentarily comoving reference frame'' (MCRF), which is to say, a frame traveling at the same instantaneous velocity of a particle at any given instant.
Consider the animation in Fig 5-1. The curved line represents the world line of a particle that undergoes continuous acceleration, including complete changes of direction in the positive and negative x-directions. The red axes are the axes of the MCRF for each point along the particle's trajectory. The coordinates of events in the unprimed (stationary) frame can be related to their coordinates in any momentarily co-moving primed frame using the Lorentz transformations.
Fig 5-2 illustrates the changing views of spacetime along the world line of a rapidly accelerating particle. The axis (not drawn) is vertical, while the axis (not drawn) is horizontal. The dashed line is the spacetime trajectory ("world line") of the particle. The balls are placed at regular intervals of proper time along the world line. The solid diagonal lines are the light cones for the observer's current event, and they intersect at that event. The small dots are other arbitrary events in the spacetime.
The slope of the world line (deviation from being vertical) is the velocity of the particle on that section of the world line. Bends in the world line represent particle acceleration. As the particle accelerates, its view of spacetime changes. These changes in view are governed by the Lorentz transformations. Also note that:
* the balls on the world line before/after future/past accelerations are more spaced out due to time dilation.
* events which were simultaneous before an acceleration (horizontally spaced events) are at different times afterwards due to the relativity of simultaneity,
* events pass through the light cone lines due to the progression of proper time, but not due to the change of views caused by the accelerations, and
* the world line always remains within the future and past light cones of the current event.
If one imagines each event to be the flashing of a light, then the events that are within the past light cone of the observer are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the velocity relative to the observer.
It is often, incorrectly, asserted that special relativity cannot handle accelerating particles or accelerating reference frames. In reality, accelerating particles present no difficulty at all in special relativity. On the other hand, accelerating ''frames'' do require some special treatment, However, as long as one is dealing with flat, Minkowskian spacetime, special relativity can handle the situation. It is only in the presence of gravitation that general relativity is required.
An accelerating particle's 4-vector acceleration is the derivative with respect to proper time of its 4-velocity. This is not a difficult situation to handle. Accelerating frames require that one understand the concept of a ''momentarily comoving reference frame'' (MCRF), which is to say, a frame traveling at the same instantaneous velocity of a particle at any given instant.
Consider the animation in Fig 5-1. The curved line represents the world line of a particle that undergoes continuous acceleration, including complete changes of direction in the positive and negative x-directions. The red axes are the axes of the MCRF for each point along the particle's trajectory. The coordinates of events in the unprimed (stationary) frame can be related to their coordinates in any momentarily co-moving primed frame using the Lorentz transformations.
Fig 5-2 illustrates the changing views of spacetime along the world line of a rapidly accelerating particle. The axis (not drawn) is vertical, while the axis (not drawn) is horizontal. The dashed line is the spacetime trajectory ("world line") of the particle. The balls are placed at regular intervals of proper time along the world line. The solid diagonal lines are the light cones for the observer's current event, and they intersect at that event. The small dots are other arbitrary events in the spacetime.
The slope of the world line (deviation from being vertical) is the velocity of the particle on that section of the world line. Bends in the world line represent particle acceleration. As the particle accelerates, its view of spacetime changes. These changes in view are governed by the Lorentz transformations. Also note that:
* the balls on the world line before/after future/past accelerations are more spaced out due to time dilation.
* events which were simultaneous before an acceleration (horizontally spaced events) are at different times afterwards due to the relativity of simultaneity,
* events pass through the light cone lines due to the progression of proper time, but not due to the change of views caused by the accelerations, and
* the world line always remains within the future and past light cones of the current event.
If one imagines each event to be the flashing of a light, then the events that are within the past light cone of the observer are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the velocity relative to the observer.
Case of non-inertial reference frames

 The photon world lines are determined using the metric with . The
The photon world lines are determined using the metric with . The light cones
In special and general relativity, a light cone (or "null cone") is the path that a flash of light, emanating from a single event (localized to a single point in space and a single moment in time) and traveling in all directions, would take thro ...
are deformed according to the position. In an inertial reference frame a free particle has a straight world line. In a non-inertial reference frame
A non-inertial reference frame is a frame of reference that undergoes acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are ...
the world line of a free particle is curved.
Let's take the example of the fall of an object dropped without initial velocity from a rocket. The rocket has a uniformly accelerated motion with respect to an inertial reference frame. As can be seen from Fig 6-2 of a Minkowski diagram in a non-inertial reference frame, the object once dropped, gains speed, reaches a maximum, and then sees its speed decrease and asymptotically cancel on the horizon
The horizon is the apparent line that separates the surface of a celestial body from its sky when viewed from the perspective of an observer on or near the surface of the relevant body. This line divides all viewing directions based on whether i ...
where its proper time freezes at . The velocity is measured by an observer at rest in the accelerated rocket.
See also
* Minkowski space * Penrose diagram *Rapidity
In relativity, rapidity is commonly used as a measure for relativistic velocity. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with di ...
References
* Anthony French (1968) ''Special Relativity'', pages 82 & 83, New York: W W Norton & Company. * E.N. Glass (1975) "Lorentz boosts and Minkowski diagrams" American Journal of Physics 43:1013,4. * N. David Mermin (1968) ''Space and Time in Special Relativity'', Chapter 17 Minkowski diagrams: The Geometry of Spacetime, pages 155–99 McGraw-Hill. * * W.G.V. Rosser (1964) ''An Introduction to the Theory of Relativity'', page 256, Figure 6.4, London:Butterworths
LexisNexis is a part of the RELX corporation that sells data analytics products and various databases that are accessed through online portals, including portals for computer-assisted legal research (CALR), newspaper search, and consumer inform ...
.
* Edwin F. Taylor
Edwin F. Taylor is an American physicist known for his contributions to the teaching of physics. Taylor was editor of the American Journal of Physics, and is author of several introductory books to physics. In 1998 he was awarded the Oersted Meda ...
and John Archibald Wheeler (1963) ''Spacetime Physics'', pages 27 to 38, New York: W. H. Freeman and Company
W. H. Freeman and Company is an imprint of Macmillan Higher Education, a division of Macmillan Publishers. Macmillan publishes monographs and textbooks for the sciences under the imprint.
History
The company was founded in 1946 by William H. ...
, Second edition (1992).
* (see page 10 of e-link)
External links
{{Relativity Special relativity Geometry Diagrams