second partial derivative test on:
[Wikipedia]
[Google]
[Amazon]
In
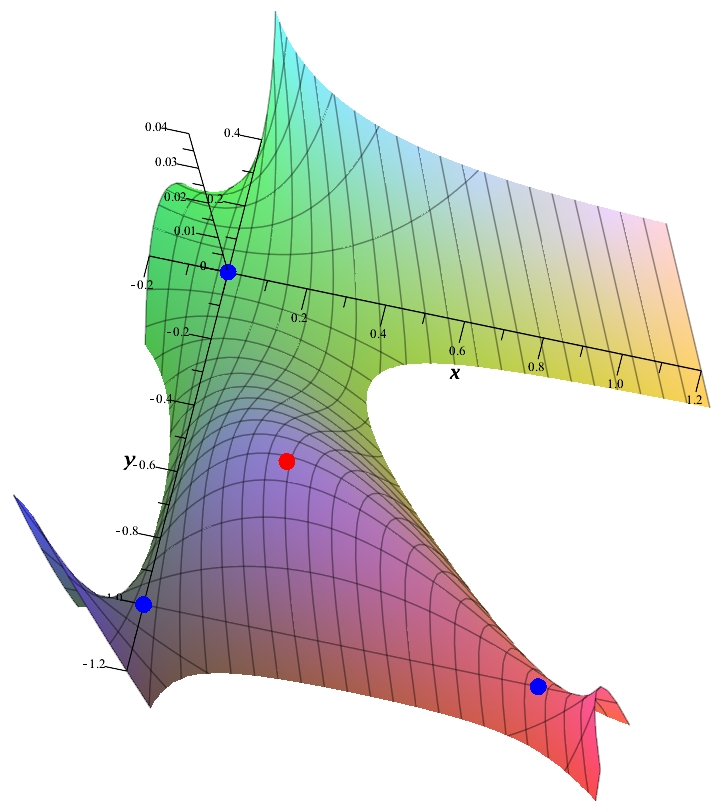 To find and classify the critical points of the function
:,
we first set the partial derivatives
: and
equal to zero and solve the resulting equations simultaneously to find the four critical points
: and .
In order to classify the critical points, we examine the value of the determinant ''D''(''x'', ''y'') of the Hessian of ''f'' at each of the four critical points. We have
:
Now we plug in all the different critical values we found to label them; we have
:
Thus, the second partial derivative test indicates that ''f''(''x'', ''y'') has saddle points at (0, −1) and (1, −1) and has a local maximum at since . At the remaining critical point (0, 0) the second derivative test is insufficient, and one must use higher order tests or other tools to determine the behavior of the function at this point. (In fact, one can show that ''f'' takes both positive and negative values in small neighborhoods around (0, 0) and so this point is a saddle point of ''f''.)
To find and classify the critical points of the function
:,
we first set the partial derivatives
: and
equal to zero and solve the resulting equations simultaneously to find the four critical points
: and .
In order to classify the critical points, we examine the value of the determinant ''D''(''x'', ''y'') of the Hessian of ''f'' at each of the four critical points. We have
:
Now we plug in all the different critical values we found to label them; we have
:
Thus, the second partial derivative test indicates that ''f''(''x'', ''y'') has saddle points at (0, −1) and (1, −1) and has a local maximum at since . At the remaining critical point (0, 0) the second derivative test is insufficient, and one must use higher order tests or other tools to determine the behavior of the function at this point. (In fact, one can show that ''f'' takes both positive and negative values in small neighborhoods around (0, 0) and so this point is a saddle point of ''f''.)
''Relative Minimums and Maximums''
- Paul's Online Math Notes - Calc III Notes (Lamar University) *{{MathWorld, title=Second Derivative Test, urlname=SecondDerivativeTest Multivariable calculus
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the second partial derivative test is a method in multivariable calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables ('' mult ...
used to determine if a critical point of a function is a local minimum
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative ...
, maximum or saddle point
In mathematics, a saddle point or minimax point is a Point (geometry), point on the surface (mathematics), surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a Critical point (mathematics), ...
.
Functions of two variables
Suppose that is a differentiablereal function
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers \mathbb, or a subset of \mathbb that contains an inter ...
of two variables whose second partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
s exist and are continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
. The Hessian matrix
In mathematics, the Hessian matrix, Hessian or (less commonly) Hesse matrix is a square matrix of second-order partial derivatives of a scalar-valued Function (mathematics), function, or scalar field. It describes the local curvature of a functio ...
of is the 2 × 2 matrix of partial derivatives of :
Define to be the determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
of . Finally, suppose that is a critical point of , that is, that . Then the second partial derivative test asserts the following:
#If and then is a local minimum of .
#If and then is a local maximum of .
#If then is a saddle point
In mathematics, a saddle point or minimax point is a Point (geometry), point on the surface (mathematics), surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a Critical point (mathematics), ...
of .
#If then the point could be any of a minimum, maximum, or saddle point (that is, the test is inconclusive).
Sometimes other equivalent versions of the test are used. In cases 1 and 2, the requirement that is positive at implies that and have the same sign there. Therefore, the second condition, that be greater (or less) than zero, could equivalently be that or be greater (or less) than zero at that point.
A condition implicit in the statement of the test is that if or , it must be the case that and therefore only cases 3 or 4 are possible.
Functions of many variables
For a function ''f'' of three or more variables, there is a generalization of the rule shown above. In this context, instead of examining the determinant of the Hessian matrix, one must look at theeigenvalues
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
of the Hessian matrix at the critical point. The following test can be applied at any critical point ''a'' for which the Hessian matrix is invertible
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
:
# If the Hessian is positive definite (equivalently, has all eigenvalues positive) at ''a'', then ''f'' attains a local minimum at ''a''.
# If the Hessian is negative definite (equivalently, has all eigenvalues negative) at ''a'', then ''f'' attains a local maximum at ''a''.
# If the Hessian has both positive and negative eigenvalues then ''a'' is a saddle point for ''f'' (and in fact this is true even if ''a'' is degenerate).
In those cases not listed above, the test is inconclusive.Kurt Endl/Wolfgang Luh: ''Analysis II''. Aula-Verlag 1972, 7th edition 1989, , pp. 248-258 (German)
For functions of three or more variables, the ''determinant'' of the Hessian does not provide enough information to classify the critical point, because the number of jointly sufficient second-order conditions is equal to the number of variables, and the sign condition on the determinant of the Hessian is only one of the conditions. Note that in the one-variable case, the Hessian condition simply gives the usual second derivative test
In calculus, a derivative test uses the derivatives of a function to locate the critical points of a function and determine whether each point is a local maximum, a local minimum, or a saddle point. Derivative tests can also give information abou ...
.
In the two variable case, and are the principal minors of the Hessian. The first two conditions listed above on the signs of these minors are the conditions for the positive or negative definiteness of the Hessian. For the general case of an arbitrary number ''n'' of variables, there are ''n'' sign conditions on the ''n'' principal minors of the Hessian matrix that together are equivalent to positive or negative definiteness of the Hessian (Sylvester's criterion
In mathematics, Sylvester’s criterion is a necessary and sufficient condition, necessary and sufficient criterion to determine whether a Hermitian matrix is Definite matrix, positive-definite.
Sylvester's criterion states that a ''n'' × ''n'' ...
): for a local minimum, all the principal minors need to be positive, while for a local maximum, the minors with an odd number of rows and columns need to be negative and the minors with an even number of rows and columns need to be positive. See Hessian matrix#Bordered Hessian for a discussion that generalizes these rules to the case of equality-constrained optimization.
Examples
 To find and classify the critical points of the function
:,
we first set the partial derivatives
: and
equal to zero and solve the resulting equations simultaneously to find the four critical points
: and .
In order to classify the critical points, we examine the value of the determinant ''D''(''x'', ''y'') of the Hessian of ''f'' at each of the four critical points. We have
:
Now we plug in all the different critical values we found to label them; we have
:
Thus, the second partial derivative test indicates that ''f''(''x'', ''y'') has saddle points at (0, −1) and (1, −1) and has a local maximum at since . At the remaining critical point (0, 0) the second derivative test is insufficient, and one must use higher order tests or other tools to determine the behavior of the function at this point. (In fact, one can show that ''f'' takes both positive and negative values in small neighborhoods around (0, 0) and so this point is a saddle point of ''f''.)
To find and classify the critical points of the function
:,
we first set the partial derivatives
: and
equal to zero and solve the resulting equations simultaneously to find the four critical points
: and .
In order to classify the critical points, we examine the value of the determinant ''D''(''x'', ''y'') of the Hessian of ''f'' at each of the four critical points. We have
:
Now we plug in all the different critical values we found to label them; we have
:
Thus, the second partial derivative test indicates that ''f''(''x'', ''y'') has saddle points at (0, −1) and (1, −1) and has a local maximum at since . At the remaining critical point (0, 0) the second derivative test is insufficient, and one must use higher order tests or other tools to determine the behavior of the function at this point. (In fact, one can show that ''f'' takes both positive and negative values in small neighborhoods around (0, 0) and so this point is a saddle point of ''f''.)
See also
*Second variation
In the calculus of variations, the second variation extends the idea of the second derivative test to functionals. Much like for functions, at a stationary point where the first derivative is zero, the second derivative determines the nature ...
Notes
References
*External links
''Relative Minimums and Maximums''
- Paul's Online Math Notes - Calc III Notes (Lamar University) *{{MathWorld, title=Second Derivative Test, urlname=SecondDerivativeTest Multivariable calculus