Riemann curvature tensor

In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.

It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving along a geodesic in a sense made precise by the Jacobi equation.

Definition

Let (''M'', g) be a Riemannian or pseudo-Riemannian manifold, and $\mathfrak(M)$ be the space of all vector fields on M. We define the ''Riemann curvature tensor'' as a map $R\colon\mathfrak(M)\times\mathfrak(M)\times\mathfrak(M)\rightarrow\mathfrak(M)$ by the following formula where $\nabla$ is an affine connection:

:$R(X, Y)Z = \nabla_X\nabla_Y Z - \nabla_Y \nabla_X Z - \nabla_ Z$

or equivalently

:R(X, Y) = nabla_X,\nabla_Y- \nabla_

where 'X'', ''Y''is the Lie bracket of vector fields and nabla_X,\nabla_Y is a commutator of differential operators. For each pair of tangent vectors ''u'', ''v'', ''R''(''u'', ''v'') is a linear transformation of the tangent space of the manifold. It is linear in ''u'' and ''v'', and so defines a tensor. Occasionally, the curvature tensor is defined with the opposite sign.

If $X = \partial/\partial x^i$ and $Y = \partial/\partial x^j$ are coordinate vector fields then , Y= 0 and therefore the formula simplifies to
:$R(X, Y)Z = \nabla_X\nabla_Y Z - \nabla_Y\nabla_X Z .$

The curvature tensor measures ''noncommutativity of the covariant derivative'', and as such is the integrability obstruction for the existence of an isometry with Euclidean space (called, in this context, ''flat'' space). The linear transformation $w \mapsto R(u, v)w$ is also called the curvature transformation or endomorphism.

The curvature formula can also be expressed in terms of the second covariant derivative defined as:

: $\nabla^2_ w = \nabla_u\nabla_v w - \nabla_ w$

which is linear in ''u'' and ''v''. Then:

: $R(u, v) = \nabla^2_ - \nabla^2_$

Thus in the general case of non-coordinate vectors ''u'' and ''v'', the curvature tensor measures the noncommutativity of the second covariant derivative.

Geometric meaning

Informally

One can see the effects of curved space by comparing a tennis court and the Earth. Start at the lower right corner of the tennis court, with a racket held out towards north. Then while walking around the outline of the court, at each step make sure the tennis racket is maintained in the same orientation, parallel to its previous positions. Once the loop is complete the tennis racket will be parallel to its initial starting position. This is because tennis courts are built so the surface is flat. On the other hand, the surface of the Earth is curved: we can complete a loop on the surface of the Earth. Starting at the equator, point a tennis racket north along the surface of the Earth. Once again the tennis racket should always remain parallel to its previous position, using the local plane of the horizon as a reference. For this path, first walk to the north pole, then turn 90 degrees and walk down to the equator, and finally turn 90 degrees and walk back to the start. However now the tennis racket will be pointing backwards (towards the east). This process is akin to parallel transporting a vector along the path and the difference identifies how lines which appear "straight" are only "straight" locally. Each time a loop is completed the tennis racket will be deflected further from its initial position by an amount depending on the distance and the curvature of the surface. It is possible to identify paths along a curved surface where parallel transport works as it does on flat space. These are the geodesic of the space, for example any segment of a great circle of a sphere.

The concept of a curved space in mathematics differs from conversational usage. For example, if the above process was completed on a cylinder one would find that it is not curved overall as the curvature around the cylinder cancels with the flatness along the cylinder, this is a consequence of Gaussian curvature and Gauss' Theorema Egregium. A familiar example of this is a floppy pizza slice which will remain rigid along its length if it is curved along its width.

The Riemann curvature tensor is a way to capture a measure of the intrinsic curvature. When you write it down in terms of its components (like writing down the components of a vector), it consists of a multi-dimensional array of sums and products of partial derivatives (some of those partial derivatives can be thought of as akin to capturing the curvature imposed upon someone walking in straight lines on a curved surface).

Formally

When a vector in a Euclidean space is parallel transported around a loop, it will again point in the initial direction after returning to its original position. However, this property does not hold in the general case. The Riemann curvature tensor directly measures the failure of this in a general Riemannian manifold. This failure is known as the non- holonomy of the manifold.

Let $x_t$ be a curve in a Riemannian manifold $M$. Denote by $\tau_:T_(M) \to T_(M)$ the parallel transport map along $x_t$. The parallel transport maps are related to the covariant derivative by
:$\nabla_ Y = \lim_ \frac\left(Y_ - \tau^_\left(Y_\right)\right) = \left.\frac\left(\tau_Y\right)\_$

for each vector field $Y$ defined along the curve.

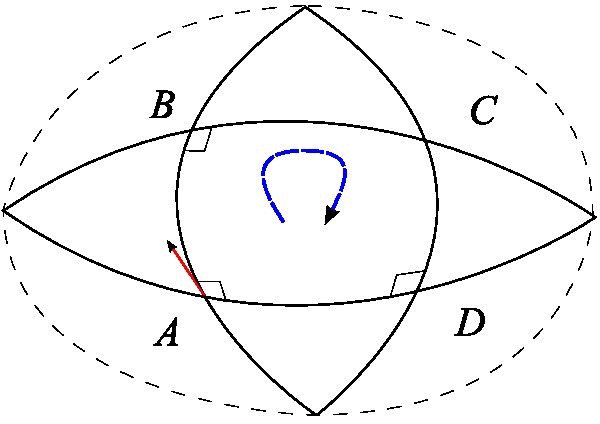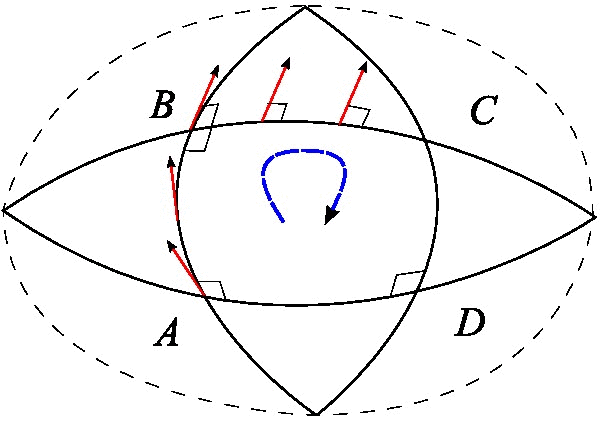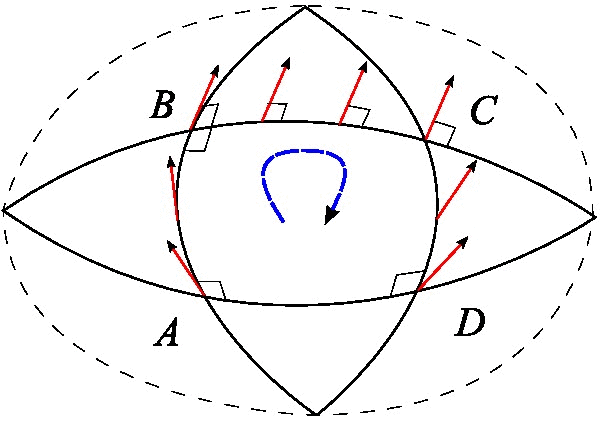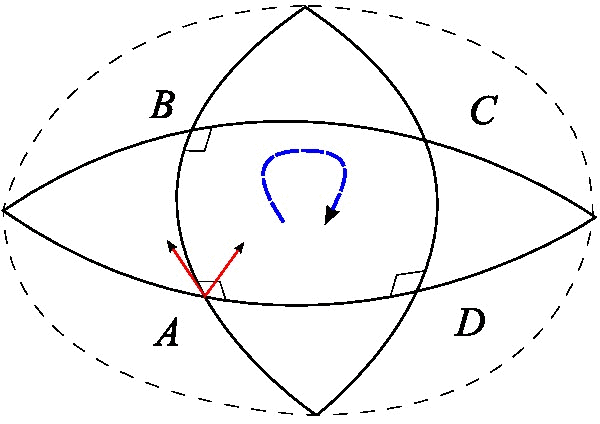
Suppose that $X$ and $Y$ are a pair of commuting vector fields. Each of these fields generates a one-parameter group of diffeomorphisms in a neighborhood of $x_0$. Denote by $\tau_$ and $\tau_$, respectively, the parallel transports along the flows of $X$ and $Y$ for time $t$. Parallel transport of a vector $Z \in T_(M)$ around the quadrilateral with sides $tY$, $sX$, $-tY$, $-sX$ is given by
:$\tau_^\tau_^\tau_\tau_Z.$

This measures the failure of parallel transport to return $Z$ to its original position in the tangent space $T_(M)$. Shrinking the loop by sending $s, t \to 0$ gives the infinitesimal description of this deviation:
:$\left.\frac\frac\tau_^\tau_^\tau_\tau_Z\_ = \left(\nabla_X\nabla_Y - \nabla_Y\nabla_X - \nabla_\right)Z = R(X, Y)Z$

where $R$ is the Riemann curvature tensor.

Coordinate expression

Converting to the tensor index notation, the Riemann curvature tensor is given by
:$R^_ = dx^\left(R\left(\partial_, \partial_\right)\partial_\right)$

where $\partial_ = \partial/\partial x^$ are the coordinate vector fields. The above expression can be written using Christoffel symbols:
:$R^_ = \partial_\Gamma^_ - \partial_\Gamma^_ + \Gamma^_\Gamma^_ - \Gamma^_\Gamma^_$

(see also the list of formulas in Riemannian geometry).

The Riemann curvature tensor is also the commutator of the covariant derivative of an arbitrary covector $A_$ with itself:
:$A_ - A_ = A_ R^_,$

since the connection $\Gamma^\alpha_$ is torsionless, which means that the torsion tensor $\Gamma^\lambda_ - \Gamma^\lambda_$ vanishes.

This formula is often called the ''Ricci identity''. This is the classical method used by Ricci and Levi-Civita to obtain an expression for the Riemann curvature tensor. In this way, the tensor character of the set of quantities $R^_$ is proved.

This identity can be generalized to get the commutators for two covariant derivatives of arbitrary tensors as follows

:\begin
&\nabla_\delta \nabla_\gamma T^_ - \nabla_\gamma \nabla_\delta T^_ \\ pt = &R^_ T^_ + \ldots +
R^_ T^_ -
R^_ T^_ - \ldots -
R^_ T^_
\end

This formula also applies to tensor densities without alteration, because for the Levi-Civita (''not generic'') connection one gets:

:$\nabla_\left(\sqrt\right) \equiv \left(\sqrt\right)_ = 0,$

where
:$g = \left, \det\left(g_\right)\.$

It is sometimes convenient to also define the purely covariant version by
:$R_ = g_ R^_.$

Symmetries and identities

The Riemann curvature tensor has the following symmetries and identities:

where the bracket $\langle,\rangle$ refers to the inner product on the tangent space induced by the metric tensor and
the brackets and parentheses on the indices denote the antisymmetrization and symmetrization operators, respectively. If there is nonzero torsion, the Bianchi identities involve the torsion tensor.

The first (algebraic) Bianchi identity was discovered by Ricci, but is often called the first Bianchi identity or algebraic Bianchi identity, because it looks similar to the differential Bianchi identity.

The first three identities form a complete list of symmetries of the curvature tensor, i.e. given any tensor which satisfies the identities above, one can find a Riemannian manifold with such a curvature tensor at some point. Simple calculations show that such a tensor has $n^2\left(n^2 - 1\right)/12$ independent components. Interchange symmetry follows from these. The algebraic symmetries are also equivalent to saying that ''R'' belongs to the image of the Young symmetrizer corresponding to the partition 2+2.

On a Riemannian manifold one has the covariant derivative $\nabla_u R$ and the Bianchi identity (often called the second Bianchi identity or differential Bianchi identity) takes the form of the last identity in the table.

Ricci curvature

The Ricci curvature tensor is the contraction of the first and third indices of the Riemann tensor.
:$\underbrace_ \equiv \underbrace_ = g^ \underbrace_$

Special cases

Surfaces

For a two-dimensional surface, the Bianchi identities imply that the Riemann tensor has only one independent component, which means that the Ricci scalar completely determines the Riemann tensor. There is only one valid expression for the Riemann tensor which fits the required symmetries:

:$R_ = f(R) \left(g_g_ - g_g_\right)$

and by contracting with the metric twice we find the explicit form:

:$R_ = K\left(g_g_ - g_g_\right) ,$

where $g_$ is the metric tensor and $K = R/2$ is a function called the Gaussian curvature and ''a'', ''b'', ''c'' and ''d'' take values either 1 or 2. The Riemann tensor has only one functionally independent component. The Gaussian curvature coincides with the sectional curvature of the surface. It is also exactly half the scalar curvature of the 2-manifold, while the Ricci curvature tensor of the surface is simply given by

:$R_ = Kg_.$

Space forms

A Riemannian manifold is a space form if its sectional curvature is equal to a constant ''K''. The Riemann tensor of a space form is given by

:$R_ = K\left(g_g_ - g_g_\right).$

Conversely, except in dimension 2, if the curvature of a Riemannian manifold has this form for some function ''K'', then the Bianchi identities imply that ''K'' is constant and thus that the manifold is (locally) a space form.

See also

* Introduction to the mathematics of general relativity
* Decomposition of the Riemann curvature tensor
* Curvature of Riemannian manifolds
*Ricci curvature tensor

Citations

References

*
*
*
*

{{DEFAULTSORT:Riemann Curvature Tensor

Bernhard Riemann
Curvature (mathematics)
Differential geometry
Riemannian geometry
Riemannian manifolds
Tensors in general relativity