Ronald Graham (mathematician)

Ronald Lewis Graham (October 31, 1935July 6, 2020) was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.

After graduate study at the University of California, Berkeley, Graham worked for many years at Bell Labs and later at the University of California, San Diego. He did important work in scheduling theory, computational geometry, Ramsey theory, and quasi-randomness, and many topics in mathematics are named after him. He published six books and about 400 papers, and had nearly 200 co-authors, including many collaborative works with his wife Fan Chung and with Paul Erdős.

Graham has been featured in ''Ripley's Believe It or Not!'' for being not only "one of the world's foremost mathematicians", but also an accomplished trampolinist and juggler. He served as president of the International Jugglers' Association.

Biography

Graham was born in Taft, California, on October 31, 1935; his father was an oil field worker and later merchant marine. Despite Graham's later interest in gymnastics, he was small and non-athletic. He grew up moving frequently between California and Georgia, skipping several grades of school in these moves, and never staying at any one school longer than a year. As a teenager, he moved to Florida with his then-divorced mother, where he went to but did not finish high school. Instead, at the age of 15, he won a Ford Foundation scholarship to the University of Chicago, where he learned gymnastics but took no mathematics courses.

After three years, when his scholarship expired, he moved to the University of California, Berkeley, officially as a student of electrical engineering but also studying number theory under D. H. Lehmer, and winning a title as California state trampoline champion. He enlisted in the United States Air Force in 1955, when he reached the age of eligibility, left Berkeley without a degree, and was stationed in Fairbanks, Alaska, where he finally completed a bachelor's degree in physics in 1959 at the University of Alaska Fairbanks. Returning to Berkeley for graduate study, he received his Ph.D. in mathematics in 1962. His dissertation, supervised by Lehmer, was ''On Finite Sums of Rational Numbers''. While a graduate student, he supported himself by performing on trampoline in a circus, and married Nancy Young, an undergraduate mathematics student at Berkeley; they had two children.

After completing his doctorate, Graham went to work in 1962 at Bell Labs and later as Director of Information Sciences at AT&T Labs, both in New Jersey. In 1963, at a conference in Colorado, he met the Hungarian mathematician Paul Erdős (1913–1996), who became a close friend and frequent research collaborator. Graham was chagrined to be beaten in ping-pong by Erdős, then already middle-aged; he returned to New Jersey determined to improve his game, and eventually became Bell Labs champion and won a state title in the game. Graham later popularized the concept of the Erdős number, a measure of distance from Erdős in the collaboration network of mathematicians; his many works with Erdős include two books of open problems and Erdős's final posthumous paper. Graham divorced in the 1970s; in 1983 he married his Bell Labs colleague and frequent coauthor Fan Chung.

While at Bell Labs, Graham also took a position at Rutgers University as University Professor of Mathematical Sciences in 1986, and served as president of the American Mathematical Society from 1993 to 1994. He became Chief Scientist of the Labs in 1995. He retired from AT&T in 1999 after 37 years of service, and moved to the University of California, San Diego (UCSD), as the Irwin and Joan Jacobs Endowed Professor of Computer and Information Science. At UCSD, he also became chief scientist at the California Institute for Telecommunications and Information Technology. In 2003–04, he was president of the Mathematical Association of America.

Graham died of bronchiectasis on July 6, 2020, aged 84, in La Jolla, California.

Contributions

Graham made important contributions in multiple areas of mathematics and theoretical computer science. He published about 400 papers, a quarter of those with Chung, and six books, including '' Concrete Mathematics'' with Donald Knuth and Oren Patashnik. The Erdős Number Project lists him as having nearly 200 coauthors. He was the doctoral advisor of nine students, one each at the City University of New York and Rutgers University while he was at Bell Labs, and seven at UC San Diego.

Notable topics in mathematics named after Graham include the Erdős–Graham problem on Egyptian fractions, the Graham–Rothschild theorem in the Ramsey theory of parameter words and Graham's number derived from it, the Graham–Pollak theorem and Graham's pebbling conjecture in graph theory, the Coffman–Graham algorithm for approximate scheduling and graph drawing, and the Graham scan algorithm for convex hulls. He also began the study of primefree sequences, the Boolean Pythagorean triples problem, the biggest little polygon, and square packing in a square.

Graham was one of the contributors to the publications of G. W. Peck, a pseudonymous mathematical collaboration named for the initials of its members, with Graham as the "G". Graham also wrote a paper on the Erdős number, pseudonymously, as Tom Odda.

Number theory

Graham's doctoral dissertation was in number theory, on Egyptian fractions, as is the Erdős–Graham problem on whether, for every partition of the integers into finitely many classes, one of these classes has a finite subclass whose reciprocals sum to one. A proof was published by Ernie Croot in 2003. Another of Graham's papers on Egyptian fractions was published in 2015 with Steve Butler and (nearly 20 years posthumously) Erdős; it was the last of Erdős's papers to be published, making Butler his 512th coauthor.

In a 1964 paper, Graham began the study of primefree sequences by observing that there exist sequences of numbers, defined by the same recurrence relation as the Fibonacci numbers, in which none of the sequence elements is prime. The challenge of constructing more such sequences was later taken up by Donald Knuth and others. Graham's 1980 book with Erdős, ''Old and new results in combinatorial number theory,'' provides a collection of open problems from a broad range of subareas within number theory.

Ramsey theory

The Graham–Rothschild theorem in Ramsey theory was published by Graham and Bruce Rothschild in 1971, and applies Ramsey theory to combinatorial cubes in combinatorics on words. Graham gave a large number as an upper bound for an instance of this theorem, now known as Graham's number, which was listed in the ''Guinness Book of Records'' as the largest number ever used in a mathematical proof, although it has since then been surpassed by even larger numbers such as TREE(3).

Graham offered a monetary prize for solving the Boolean Pythagorean triples problem, another problem in Ramsey theory; the prize was claimed in 2016.
Graham also published two books on Ramsey theory.

Graph theory

The Graham–Pollak theorem, which Graham published with Henry O. Pollak in two papers in 1971 and 1972, states that if the edges of an $n$-vertex complete graph are partitioned into complete bipartite subgraphs, then at least $n-1$ subgraphs are needed. Graham and Pollak provided a simple proof using linear algebra; despite the combinatorial nature of the statement and multiple publications of alternative proofs since their work, all known proofs require linear algebra.

Soon after research in quasi-random graphs began with the work of Andrew Thomason, Graham published in 1989 a result with Chung and R. M. Wilson that has been called the "fundamental theorem of quasi-random graphs", stating that many different definitions of these graphs are equivalent.

Graham's pebbling conjecture, appearing in a 1989 paper by Chung, is an open problem on the pebbling number of Cartesian products of graphs.

Packing, scheduling, and approximation algorithms

Graham's early work on job shop scheduling introduced the worst-case approximation ratio into the study of approximation algorithms, and laid the foundations for the later development of competitive analysis of online algorithms. This work was later recognized to be important also for the theory of bin packing, an area that Graham later worked in more explicitly.

The Coffman–Graham algorithm, which Graham published with Edward G. Coffman Jr. in 1972, provides an optimal algorithm for two-machine scheduling, and a guaranteed approximation algorithm for larger numbers of machines. It has also been applied in layered graph drawing.

In a survey article on scheduling algorithms published in 1979, Graham and his coauthors introduced a three-symbol notation for classifying theoretical scheduling problems according to the system of machines they are to run on, the characteristics of the tasks and resources such as requirements for synchronization or non-interruption, and the performance measure to be optimized. This classification has sometimes been called "Graham notation" or "Graham's notation".

Discrete and computational geometry

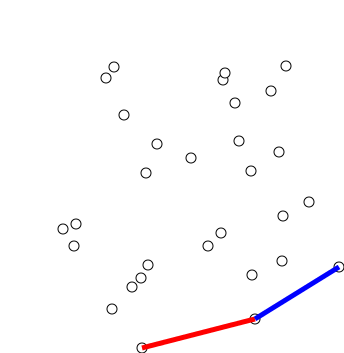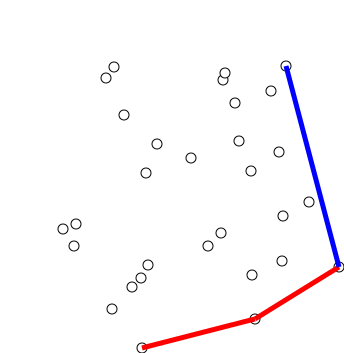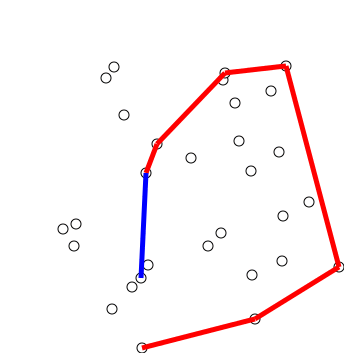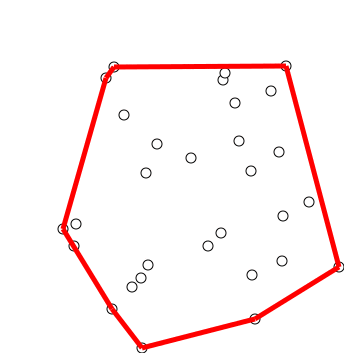
Graham scan is a widely used and practical algorithm for convex hulls of two-dimensional point sets, based on sorting the points and then inserting them into the hull in sorted order. Graham published the algorithm in 1972.

The biggest little polygon problem asks for the polygon of largest area for a given diameter. Surprisingly, as Graham observed, the answer is not always a regular polygon. Graham's 1975 conjecture on the shape of these polygons was finally proven in 2007.

In another 1975 publication, Graham and Erdős observed that for packing unit squares into a larger square with non-integer side lengths, one can use tilted squares to leave an uncovered area that is sublinear in the side length of the larger square, unlike the obvious packing with axis-aligned squares. Klaus Roth and Bob Vaughan proved that uncovered area at least proportional to the square root of the side length may sometimes be needed; proving a tight bound on the uncovered area remains an open problem.

Probability and statistics

In nonparametric statistics, a 1977 paper by Persi Diaconis and Graham studied the statistical properties of Spearman's footrule, a measure of rank correlation that compares two permutations by summing, over each item, the distance between the positions of the item in the two permutations.
They compared this measure to other rank correlation methods, resulting in the "Diaconis–Graham inequalities"
:$I+E\le D\le 2I$
where $D$ is Spearman's footrule, $I$ is the number of inversions between the two permutations (a non-normalized version of the Kendall rank correlation coefficient), and $E$ is the minimum number of two-element swaps needed to obtain one permutation from the other.

The Chung–Diaconis–Graham random process is a random walk on the integers modulo an odd integer $p$, in which at each step one doubles the previous number and then randomly adds zero, $1$, or $-1$ (modulo $p$). In a 1987 paper, Chung, Diaconis, and Graham studied the mixing time of this process, motivated by the study of pseudorandom number generators.

Juggling

Graham became a capable juggler beginning at age 15, and was practiced in juggling up to six balls. (Although a published photo shows him juggling twelve balls, it is a manipulated image.) He taught Steve Mills, a repeat winner of the International Jugglers' Association championships, how to juggle, and his work with Mills helped inspire Mills to develop the Mills' Mess juggling pattern. As well, Graham made significant contributions to the theory of juggling, including a sequence of publications on siteswaps. In 1972 he was elected president of the International Jugglers' Association.

Awards and honors

In 2003, Graham won the American Mathematical Society's annual Leroy P. Steele Prize for Lifetime Achievement. The prize cited his contributions to discrete mathematics, his popularization of mathematics through his talks and writing, his leadership at Bell Labs, and his service as president of the society. He was one of five inaugural winners of the George Pólya Prize of the Society for Industrial and Applied Mathematics, sharing it with fellow Ramsey theorists Klaus Leeb, Bruce Rothschild, Alfred Hales, and Robert I. Jewett. He was also one of two inaugural winners of the Euler Medal of the Institute of Combinatorics and its Applications, the other being Claude Berge.

Graham was elected to the National Academy of Sciences in 1985. In 1999 he was inducted as an ACM Fellow "for seminal contributions to the analysis of algorithms, in particular the worst-case analysis of heuristics, the theory of scheduling, and computational geometry". He became a Fellow of the Society for Industrial and Applied Mathematics in 2009; the fellow award cited his "contributions to discrete mathematics and its applications". In 2012 he became a fellow of the American Mathematical Society.

Graham was an invited speaker at the 1982 International Congress of Mathematicians (held 1983 in Warsaw), speaking on "Recent developments in Ramsey theory". He was twice Josiah Willard Gibbs Lecturer, in 2001 and 2015.
The Mathematical Association of America awarded him both the Carl Allendoerfer Prize for his paper "Steiner Trees on a Checkerboard" with Chung and Martin Gardner in ''Mathematics Magazine'' (1989), and the Lester R. Ford Award for his paper "A whirlwind tour of computational geometry" with Frances Yao in the ''American Mathematical Monthly'' (1990). His book ''Magical Mathematics'' with Persi Diaconis won the Euler Book Prize.

The proceedings of the ''Integers 2005'' conference was published as a festschrift for Ron Graham's 70th birthday. Another festschrift, stemming from a conference held in 2015 in honor of Graham's 80th birthday, was published in 2018 as the book ''Connections in discrete mathematics: a celebration of the work of Ron Graham''. Reviews:

Selected publications

Books

Edited volumes

Articles

References

External links

Graham's UCSD Faculty Research Profile

Papers of Ron Graham
a comprehensive archive of the papers written by Ron Graham

About Ron Graham
a page summarizing some aspects of Graham's life and mathematics part o
Fan Chung's website
* – Extended video interview.

"Three Mathematicians We Lost in 2020: John Conway, Ronald Graham, and Freeman Dyson all explored the world with their minds"
Rockmore, Dan. (December 31, 2020) ''The New Yorker''.
*
*

{{DEFAULTSORT:Graham, Ronald
1935 births
2020 deaths
20th-century American mathematicians
21st-century American mathematicians
Fellows of the American Mathematical Society
1999 fellows of the Association for Computing Machinery
Fellows of the Society for Industrial and Applied Mathematics
Graph theorists
Mathematicians from California
Mathematics popularizers
Members of the United States National Academy of Sciences
People from Taft, California
Presidents of the American Mathematical Society
Presidents of the Mathematical Association of America
Researchers in geometric algorithms
Scientists at Bell Labs
University of Alaska Fairbanks alumni
University of California, Berkeley alumni
Rutgers University faculty
University of California, San Diego faculty
Deaths from lung disease