relativity of simultaneity on:
[Wikipedia]
[Google]
[Amazon]


 In
In
 Einstein's version of the experiment presumed that one observer was sitting midway inside a speeding traincar and another was standing on a platform as the train moved past. As measured by the standing observer, the train is struck by two bolts of lightning simultaneously, but at different positions along the axis of train movement (back and front of the train car). In the inertial frame of the standing observer, there are three events which are spatially dislocated, but simultaneous: standing observer facing the moving observer (i.e., the center of the train), lightning striking the front of the train car, and lightning striking the back of the car.
Since the events are placed along the axis of train movement, their time coordinates become projected to different time coordinates in the moving train's inertial frame. Events which occurred at space coordinates in the direction of train movement happen ''earlier'' than events at coordinates opposite to the direction of train movement. In the moving train's inertial frame, this means that lightning will strike the front of the train car ''before'' the two observers align (face each other).
Einstein's version of the experiment presumed that one observer was sitting midway inside a speeding traincar and another was standing on a platform as the train moved past. As measured by the standing observer, the train is struck by two bolts of lightning simultaneously, but at different positions along the axis of train movement (back and front of the train car). In the inertial frame of the standing observer, there are three events which are spatially dislocated, but simultaneous: standing observer facing the moving observer (i.e., the center of the train), lightning striking the front of the train car, and lightning striking the back of the car.
Since the events are placed along the axis of train movement, their time coordinates become projected to different time coordinates in the moving train's inertial frame. Events which occurred at space coordinates in the direction of train movement happen ''earlier'' than events at coordinates opposite to the direction of train movement. In the moving train's inertial frame, this means that lightning will strike the front of the train car ''before'' the two observers align (face each other).

 A popular picture for understanding this idea is provided by a thought experiment similar to those suggested by Daniel Frost Comstock in 1910 and Einstein in 1917.Einstein's thought experiment used two light rays starting at both ends of the platform. See:
A popular picture for understanding this idea is provided by a thought experiment similar to those suggested by Daniel Frost Comstock in 1910 and Einstein in 1917.Einstein's thought experiment used two light rays starting at both ends of the platform. See:
Chapter IX
It also consists of one observer midway inside a speeding traincar and another observer standing on a platform as the train moves past. A flash of light is given off at the center of the traincar just as the two observers pass each other. For the observer on board the train, the front and back of the traincar are at fixed distances from the light source and as such, according to this observer, the light will reach the front and back of the traincar at the same time. For the observer standing on the platform, on the other hand, the rear of the traincar is moving (catching up) toward the point at which the flash was given off, and the front of the traincar is moving away from it. As the speed of light is, according to the second postulate of special relativity, same in all directions for all observers, the light headed for the back of the train will have less distance to cover than the light headed for the front. Thus, the flashes of light will strike the ends of the traincar at different times.

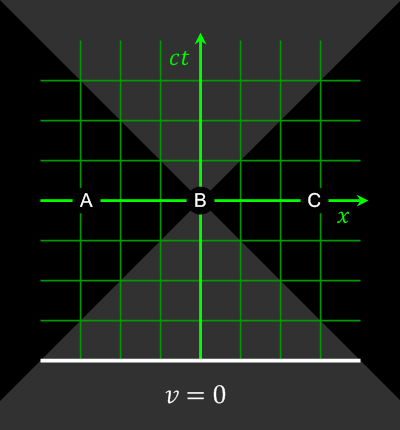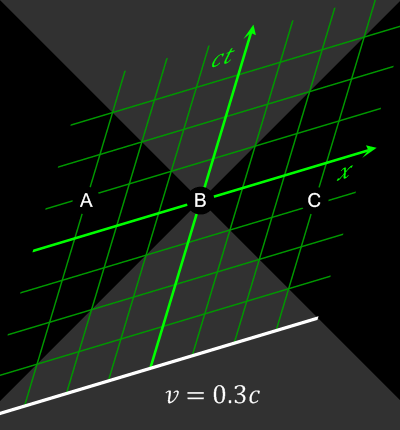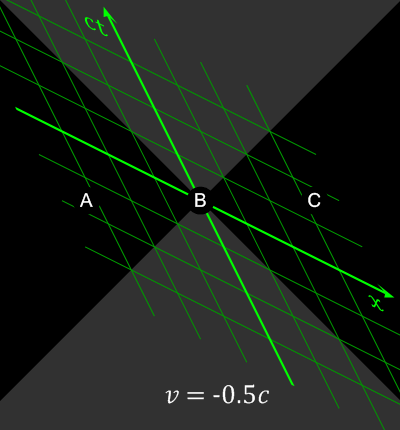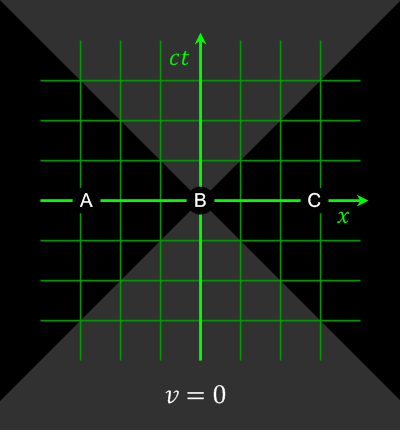
 The equation ''t′'' = constant defines a "line of simultaneity" in the (''x′'', ''t′'') coordinate system for the second (moving) observer, just as the equation ''t'' = constant defines the "line of simultaneity" for the first (stationary) observer in the (''x'', ''t'') coordinate system. From the above equations for the Lorentz transform it can be seen that ''t is constant if and only if ''t'' − ''vx''/''c''2 = constant. Thus the set of points that make ''t'' constant are different from the set of points that makes ''t' ''constant. That is, the set of events which are regarded as simultaneous depends on the frame of reference used to make the comparison.
Graphically, this can be represented on a spacetime diagram by the fact that a plot of the set of points regarded as simultaneous generates a line which depends on the observer. In the spacetime diagram, the dashed line represents a set of points considered to be simultaneous with the origin by an observer moving with a velocity ''v'' of one-quarter of the speed of light. The dotted horizontal line represents the set of points regarded as simultaneous with the origin by a stationary observer. This diagram is drawn using the (''x'', ''t'') coordinates of the stationary observer, and is scaled so that the speed of light is one, i.e., so that a ray of light would be represented by a line with a 45° angle from the ''x'' axis. From our previous analysis, given that ''v'' = 0.25 and ''c'' = 1, the equation of the dashed line of simultaneity is ''t'' − 0.25''x'' = 0 and with ''v'' = 0, the equation of the dotted line of simultaneity is ''t'' = 0.
In general the second observer traces out a worldline in the spacetime of the first observer described by ''t'' = ''x''/''v'', and the set of simultaneous events for the second observer (at the origin) is described by the line ''t'' = ''vx''. Note the
The equation ''t′'' = constant defines a "line of simultaneity" in the (''x′'', ''t′'') coordinate system for the second (moving) observer, just as the equation ''t'' = constant defines the "line of simultaneity" for the first (stationary) observer in the (''x'', ''t'') coordinate system. From the above equations for the Lorentz transform it can be seen that ''t is constant if and only if ''t'' − ''vx''/''c''2 = constant. Thus the set of points that make ''t'' constant are different from the set of points that makes ''t' ''constant. That is, the set of events which are regarded as simultaneous depends on the frame of reference used to make the comparison.
Graphically, this can be represented on a spacetime diagram by the fact that a plot of the set of points regarded as simultaneous generates a line which depends on the observer. In the spacetime diagram, the dashed line represents a set of points considered to be simultaneous with the origin by an observer moving with a velocity ''v'' of one-quarter of the speed of light. The dotted horizontal line represents the set of points regarded as simultaneous with the origin by a stationary observer. This diagram is drawn using the (''x'', ''t'') coordinates of the stationary observer, and is scaled so that the speed of light is one, i.e., so that a ray of light would be represented by a line with a 45° angle from the ''x'' axis. From our previous analysis, given that ''v'' = 0.25 and ''c'' = 1, the equation of the dashed line of simultaneity is ''t'' − 0.25''x'' = 0 and with ''v'' = 0, the equation of the dotted line of simultaneity is ''t'' = 0.
In general the second observer traces out a worldline in the spacetime of the first observer described by ''t'' = ''x''/''v'', and the set of simultaneous events for the second observer (at the origin) is described by the line ''t'' = ''vx''. Note the
 The Lorentz-transform calculation above uses a definition of extended-simultaneity (i.e. of when and where events occur ''at which you were not present'') that might be referred to as the co-moving or "tangent free-float-frame" definition. This definition is naturally extrapolated to events in gravitationally-curved spacetimes, and to accelerated observers, through use of a radar-time/distance definition that (unlike the tangent free-float-frame definition for accelerated frames) assigns a unique time and position to any event.
The radar-time definition of extended-simultaneity further facilitates visualization of the way that acceleration curves spacetime for travelers in the absence of any gravitating objects. This is illustrated in the figure at right, which shows radar time/position isocontours for events in flat spacetime as experienced by a traveler (red trajectory) taking a constant proper-acceleration roundtrip. One caveat of this approach is that the time and place of remote events are not fully defined until light from such an event is able to reach our traveler.
The Lorentz-transform calculation above uses a definition of extended-simultaneity (i.e. of when and where events occur ''at which you were not present'') that might be referred to as the co-moving or "tangent free-float-frame" definition. This definition is naturally extrapolated to events in gravitationally-curved spacetimes, and to accelerated observers, through use of a radar-time/distance definition that (unlike the tangent free-float-frame definition for accelerated frames) assigns a unique time and position to any event.
The radar-time definition of extended-simultaneity further facilitates visualization of the way that acceleration curves spacetime for travelers in the absence of any gravitating objects. This is illustrated in the figure at right, which shows radar time/position isocontours for events in flat spacetime as experienced by a traveler (red trajectory) taking a constant proper-acceleration roundtrip. One caveat of this approach is that the time and place of remote events are not fully defined until light from such an event is able to reach our traveler.

 In
In physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, the relativity of simultaneity is the concept that ''distant simultaneity'' – whether two spatially separated events occur at the same time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
– is not absolute, but depends on the observer's reference frame. This possibility was raised by mathematician Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
in 1900, and thereafter became a central idea in the special theory of relativity.
Description
According to the special theory of relativity introduced byAlbert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
, it is impossible to say in an ''absolute'' sense that two distinct events occur at the same time if those events are separated in space. If one reference frame assigns precisely the same time to two events that are at different points in space, a reference frame that is moving relative to the first will generally assign different times to the two events (the only exception being when motion is exactly perpendicular to the line connecting the locations of both events).
For example, a car crash in London and another in New York that appear to happen at the same time to an observer on Earth will appear to have occurred at slightly different times to an observer on an airplane flying between London and New York. Furthermore, if the two events cannot be causally connected, depending on the state of motion, the crash in London may appear to occur first in a given frame, and the New York crash may appear to occur first in another. However, if the events can be causally connected, precedence order is preserved in all frames of reference.
History
In 1892 and 1895, Hendrik Lorentz used a mathematical method called "local time" ''t' = t – v x/c''2 for explaining the negative aether drift experiments. However, Lorentz gave no physical explanation of this effect. This was done byHenri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
who already emphasized in 1898 the conventional nature of simultaneity and who argued that it is convenient to postulate the constancy of the speed of light in all directions. However, this paper did not contain any discussion of Lorentz's theory or the possible difference in defining simultaneity for observers in different states of motion.
This was done in 1900, when Poincaré derived local time by assuming that the speed of light is invariant within the aether. Due to the "principle of relative motion", moving observers within the aether also assume that they are at rest and that the speed of light is constant in all directions (only to first order in ''v/c''). Therefore, if they synchronize their clocks by using light signals, they will only consider the transit time for the signals, but not their motion in respect to the aether. So the moving clocks are not synchronous and do not indicate the "true" time. Poincaré calculated that this synchronization error corresponds to Lorentz's local time.
In 1904, Poincaré emphasized the connection between the principle of relativity, "local time", and light speed invariance; however, the reasoning in that paper was presented in a qualitative and conjectural manner.
Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
used a similar method in 1905 to derive the time transformation for all orders in ''v/c'', i.e., the complete Lorentz transformation. Poincaré obtained the full transformation earlier in 1905 but in the papers of that year he did not mention his synchronization procedure. This derivation was completely based on light speed invariance and the relativity principle, so Einstein noted that for the electrodynamics of moving bodies the aether is superfluous. Thus, the separation into "true" and "local" times of Lorentz and Poincaré vanishes – all times are equally valid and therefore the relativity of length and time is a natural consequence.
In 1908, Hermann Minkowski introduced the concept of a world line
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept of modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from c ...
of a particle in his model of the cosmos called Minkowski space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a ...
. In Minkowski's view, the naïve notion of velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
is replaced with rapidity
In special relativity, the classical concept of velocity is converted to rapidity to accommodate the limit determined by the speed of light. Velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velo ...
, and the ordinary sense of simultaneity becomes dependent on hyperbolic orthogonality
In geometry, the relation of hyperbolic orthogonality between two lines separated by the asymptotes of a hyperbola is a concept used in special relativity to define simultaneous events. Two events will be simultaneous when they are on a line hyp ...
of spatial directions to the worldline associated to the rapidity. Then every inertial frame of reference
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative ...
has a rapidity and a simultaneous hyperplane.
In 1990, Robert Goldblatt
__NOTOC__
Robert Ian Goldblatt (born 1949) is a mathematical logician who is emeritus Professor in the School of Mathematics and Statistics at Victoria University, Wellington, New Zealand. His doctoral advisor was Max Cresswell. His most popula ...
wrote ''Orthogonality and Spacetime Geometry'', directly addressing the structure Minkowski had put in place for simultaneity. In 2006, Max Jammer
Max Jammer (; born Moshe Jammer, ; 13 April 1915 – 18 December 2010), was an Israeli physicist and philosophy of physics, philosopher of physics. He was born in Berlin, Germany. He was Rector and Acting President at Bar-Ilan University from 19 ...
, through Project MUSE, published ''Concepts of Simultaneity: from antiquity to Einstein and beyond''. The book culminates in chapter 6, "The transition to the relativistic conception of simultaneity". Jammer indicates that Ernst Mach
Ernst Waldfried Josef Wenzel Mach ( ; ; 18 February 1838 – 19 February 1916) was an Austrian physicist and philosopher, who contributed to the understanding of the physics of shock waves. The ratio of the speed of a flow or object to that of ...
demythologized the absolute time of Newtonian physics.
Naturally the mathematical notions preceded physical interpretation. For instance, conjugate diameters
In geometry, two diameters of a conic section are said to be conjugate if each chord (geometry), chord parallel (geometry), parallel to one diameter is bisection, bisected by the other diameter. For example, two diameters of a circle are conjugate ...
of conjugate hyperbolas are related as space and time. The principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference.
For example, in the framework of special relativity, the Maxwell equations ...
can be expressed as the arbitrariness of which pair are taken to represent space and time in a plane.
Thought experiments
Einstein's train
 Einstein's version of the experiment presumed that one observer was sitting midway inside a speeding traincar and another was standing on a platform as the train moved past. As measured by the standing observer, the train is struck by two bolts of lightning simultaneously, but at different positions along the axis of train movement (back and front of the train car). In the inertial frame of the standing observer, there are three events which are spatially dislocated, but simultaneous: standing observer facing the moving observer (i.e., the center of the train), lightning striking the front of the train car, and lightning striking the back of the car.
Since the events are placed along the axis of train movement, their time coordinates become projected to different time coordinates in the moving train's inertial frame. Events which occurred at space coordinates in the direction of train movement happen ''earlier'' than events at coordinates opposite to the direction of train movement. In the moving train's inertial frame, this means that lightning will strike the front of the train car ''before'' the two observers align (face each other).
Einstein's version of the experiment presumed that one observer was sitting midway inside a speeding traincar and another was standing on a platform as the train moved past. As measured by the standing observer, the train is struck by two bolts of lightning simultaneously, but at different positions along the axis of train movement (back and front of the train car). In the inertial frame of the standing observer, there are three events which are spatially dislocated, but simultaneous: standing observer facing the moving observer (i.e., the center of the train), lightning striking the front of the train car, and lightning striking the back of the car.
Since the events are placed along the axis of train movement, their time coordinates become projected to different time coordinates in the moving train's inertial frame. Events which occurred at space coordinates in the direction of train movement happen ''earlier'' than events at coordinates opposite to the direction of train movement. In the moving train's inertial frame, this means that lightning will strike the front of the train car ''before'' the two observers align (face each other).
The train-and-platform
Chapter IX
It also consists of one observer midway inside a speeding traincar and another observer standing on a platform as the train moves past. A flash of light is given off at the center of the traincar just as the two observers pass each other. For the observer on board the train, the front and back of the traincar are at fixed distances from the light source and as such, according to this observer, the light will reach the front and back of the traincar at the same time. For the observer standing on the platform, on the other hand, the rear of the traincar is moving (catching up) toward the point at which the flash was given off, and the front of the traincar is moving away from it. As the speed of light is, according to the second postulate of special relativity, same in all directions for all observers, the light headed for the back of the train will have less distance to cover than the light headed for the front. Thus, the flashes of light will strike the ends of the traincar at different times.
Spacetime diagrams
It may be helpful to visualize this situation usingspacetime diagram
A spacetime diagram is a graphical illustration of locations in space at various times, especially in the special theory of relativity. Spacetime diagrams can show the geometry underlying phenomena like time dilation and length contraction witho ...
s. For a given observer, the ''t''-axis is defined to be a point traced out in time by the origin of the spatial coordinate ''x'', and is drawn vertically. The ''x''-axis is defined as the set of all points in space at the time ''t'' = 0, and is drawn horizontally. The statement that the speed of light is the same for all observers is represented by drawing a light ray as a 45° line, regardless of the speed of the source relative to the speed of the observer.
In the first diagram, the two ends of the train are drawn as grey lines. Because the ends of the train are stationary with respect to the observer on the train, these lines are just vertical lines, showing their motion through time but not space. The flash of light is shown as the 45° red lines. The points at which the two light flashes hit the ends of the train are at the same level in the diagram. This means that the events are simultaneous.
In the second diagram, the two ends of the train moving to the right, are shown by parallel lines. The flash of light is given off at a point exactly halfway between the two ends of the train, and again form two 45° lines, expressing the constancy of the speed of light. In this picture, however, the points at which the light flashes hit the ends of the train are ''not'' at the same level; they are ''not'' simultaneous.
Lorentz transformation
The relativity of simultaneity can be demonstrated using the Lorentz transformation, which relates the coordinates used by one observer to coordinates used by another in uniform relative motion with respect to the first. Assume that the first observer uses coordinates labeled ''t'', ''x'', ''y'', and ''z'', while the second observer uses coordinates labeled ''t′'', ''x′'', ''y′'', and ''z′''. Now suppose that the first observer sees the second observer moving in the ''x''-direction at a velocity ''v''. And suppose that the observers' coordinate axes are parallel and that they have the same origin. Then the Lorentz transformation expresses how the coordinates are related: where ''c'' is thespeed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
. If two events happen at the same time in the frame of the first observer, they will have identical values of the ''t''-coordinate. However, if they have different values of the ''x''-coordinate (different positions in the ''x''-direction), they will have different values of the ''t coordinate, so they will happen at different times in that frame. The term that accounts for the failure of absolute simultaneity is the ''vx''/''c''2.
multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a ra ...
relation of the slope
In mathematics, the slope or gradient of a Line (mathematics), line is a number that describes the direction (geometry), direction of the line on a plane (geometry), plane. Often denoted by the letter ''m'', slope is calculated as the ratio of t ...
s of the worldline and simultaneous events, in accord with the principle of hyperbolic orthogonality
In geometry, the relation of hyperbolic orthogonality between two lines separated by the asymptotes of a hyperbola is a concept used in special relativity to define simultaneous events. Two events will be simultaneous when they are on a line hyp ...
.
Accelerated observers
 The Lorentz-transform calculation above uses a definition of extended-simultaneity (i.e. of when and where events occur ''at which you were not present'') that might be referred to as the co-moving or "tangent free-float-frame" definition. This definition is naturally extrapolated to events in gravitationally-curved spacetimes, and to accelerated observers, through use of a radar-time/distance definition that (unlike the tangent free-float-frame definition for accelerated frames) assigns a unique time and position to any event.
The radar-time definition of extended-simultaneity further facilitates visualization of the way that acceleration curves spacetime for travelers in the absence of any gravitating objects. This is illustrated in the figure at right, which shows radar time/position isocontours for events in flat spacetime as experienced by a traveler (red trajectory) taking a constant proper-acceleration roundtrip. One caveat of this approach is that the time and place of remote events are not fully defined until light from such an event is able to reach our traveler.
The Lorentz-transform calculation above uses a definition of extended-simultaneity (i.e. of when and where events occur ''at which you were not present'') that might be referred to as the co-moving or "tangent free-float-frame" definition. This definition is naturally extrapolated to events in gravitationally-curved spacetimes, and to accelerated observers, through use of a radar-time/distance definition that (unlike the tangent free-float-frame definition for accelerated frames) assigns a unique time and position to any event.
The radar-time definition of extended-simultaneity further facilitates visualization of the way that acceleration curves spacetime for travelers in the absence of any gravitating objects. This is illustrated in the figure at right, which shows radar time/position isocontours for events in flat spacetime as experienced by a traveler (red trajectory) taking a constant proper-acceleration roundtrip. One caveat of this approach is that the time and place of remote events are not fully defined until light from such an event is able to reach our traveler.
See also
* Andromeda paradox *Causal structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the possible causal relationships between points in the manifold.
Lorentzian manifolds can be classified according to the types of causal structures they admit (''c ...
* Einstein's thought experiments
* Ehrenfest's paradox
* Einstein synchronisation
References
External links
* {{Relativity Simultaneity History of physics Thought experiments in physics