Quantum Revival on:
[Wikipedia]
[Google]
[Amazon]
 In quantum mechanics, the quantum revival
is a periodic recurrence of the quantum wave function
from its original form during the time evolution either many times in space as the multiple scaled fractions
in the form of the initial wave function (fractional revival) or approximately or exactly to its original
form from the beginning (full revival). The quantum wave function periodic in time exhibits therefore the full revival
every Period (physics), period. The phenomenon of revivals is most readily observable for the wave functions being Trojan wave packet, well localized wave packets at the beginning of the time evolution for example in the hydrogen atom. For Hydrogen, the fractional revivals show up
as multiple angular Gaussian bumps around the circle drawn by the radial maximum of leading Hydrogen atom, circular state component (that with the highest amplitude in the eigenstate expansion) of the
original localized state and the full revival as the original Gaussian.
The full revivals are exact for the infinite quantum well, quantum harmonic oscillator, harmonic oscillator or the hydrogen atom, while for shorter times are approximate
for the hydrogen atom and a lot of quantum systems.
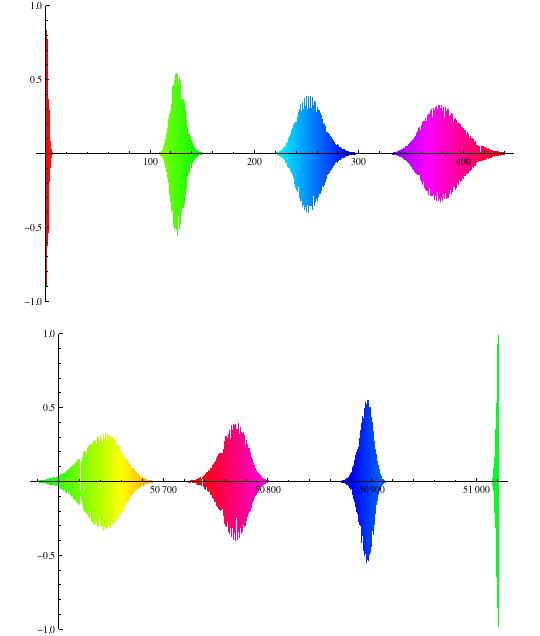
The plot of collapses and revivals of quantum oscillations of the JCM atomic inversion.
In quantum mechanics, the quantum revival
is a periodic recurrence of the quantum wave function
from its original form during the time evolution either many times in space as the multiple scaled fractions
in the form of the initial wave function (fractional revival) or approximately or exactly to its original
form from the beginning (full revival). The quantum wave function periodic in time exhibits therefore the full revival
every Period (physics), period. The phenomenon of revivals is most readily observable for the wave functions being Trojan wave packet, well localized wave packets at the beginning of the time evolution for example in the hydrogen atom. For Hydrogen, the fractional revivals show up
as multiple angular Gaussian bumps around the circle drawn by the radial maximum of leading Hydrogen atom, circular state component (that with the highest amplitude in the eigenstate expansion) of the
original localized state and the full revival as the original Gaussian.
The full revivals are exact for the infinite quantum well, quantum harmonic oscillator, harmonic oscillator or the hydrogen atom, while for shorter times are approximate
for the hydrogen atom and a lot of quantum systems.
The plot of collapses and revivals of quantum oscillations of the JCM atomic inversion.
 .
Let be to lowest common multiple of all and greatest common divisor of all
then for each the is an integer, for each the is an integer, is the full multiple of angle and
:
after the full revival time time
:.
For the quantum system as small as Hydrogen and as small as 100 it may take quadrillions of years till it will fully revive. Especially once created by fields the Trojan wave packet in a
hydrogen atom exists without any external fields
Stroboscopic effect, stroboscopically and eternally repeating itself
after sweeping almost the whole hypercube of quantum phases exactly every full revival time.
The striking consequence is that no finite-bit computer can propagate the numerical wave function accurately for the arbitrarily long
time. If the processor number is n-bit long floating point number then the number can be stored by the computer only with the finite accuracy after the comma and the energy is (up to 8 digits after the comma) for example 2.34576893 = 234576893/100000000 and as the finite fraction it
is exactly rational and the full revival occurs for any wave function of any quantum system after the time which is its maximum exponent and so on that may not be true for all quantum systems or all stationary quantum systems undergo the full and exact revival numerically.
In the system with the rational energies i.e. where the quantum exact full revival exists its existence immediately proves the quantum Poincaré recurrence theorem and the time of the full quantum revival equals to the Poincaré recurrence time.
While the rational numbers are dense set, dense in real numbers and the arbitrary function of
the quantum number can be approximated arbitrarily exactly with Padé approximants with the
coefficients of arbitrary decimal precision for the arbitrarily long time each quantum system therefore revives
almost exactly. It also means that the Poincaré recurrence and the full revival is mathematically the same thing and it is
commonly accepted that the recurrence is called the full revival if it occurs after the reasonable and physically measurable time
that is possible to be detected by the realistic apparatus and this happens due to a very special energy spectrum having a large basic energy
spacing gap of which the energies are arbitrary (not necessarily harmonic) multiples.
.
Let be to lowest common multiple of all and greatest common divisor of all
then for each the is an integer, for each the is an integer, is the full multiple of angle and
:
after the full revival time time
:.
For the quantum system as small as Hydrogen and as small as 100 it may take quadrillions of years till it will fully revive. Especially once created by fields the Trojan wave packet in a
hydrogen atom exists without any external fields
Stroboscopic effect, stroboscopically and eternally repeating itself
after sweeping almost the whole hypercube of quantum phases exactly every full revival time.
The striking consequence is that no finite-bit computer can propagate the numerical wave function accurately for the arbitrarily long
time. If the processor number is n-bit long floating point number then the number can be stored by the computer only with the finite accuracy after the comma and the energy is (up to 8 digits after the comma) for example 2.34576893 = 234576893/100000000 and as the finite fraction it
is exactly rational and the full revival occurs for any wave function of any quantum system after the time which is its maximum exponent and so on that may not be true for all quantum systems or all stationary quantum systems undergo the full and exact revival numerically.
In the system with the rational energies i.e. where the quantum exact full revival exists its existence immediately proves the quantum Poincaré recurrence theorem and the time of the full quantum revival equals to the Poincaré recurrence time.
While the rational numbers are dense set, dense in real numbers and the arbitrary function of
the quantum number can be approximated arbitrarily exactly with Padé approximants with the
coefficients of arbitrary decimal precision for the arbitrarily long time each quantum system therefore revives
almost exactly. It also means that the Poincaré recurrence and the full revival is mathematically the same thing and it is
commonly accepted that the recurrence is called the full revival if it occurs after the reasonable and physically measurable time
that is possible to be detected by the realistic apparatus and this happens due to a very special energy spectrum having a large basic energy
spacing gap of which the energies are arbitrary (not necessarily harmonic) multiples.
 In quantum mechanics, the quantum revival
is a periodic recurrence of the quantum wave function
from its original form during the time evolution either many times in space as the multiple scaled fractions
in the form of the initial wave function (fractional revival) or approximately or exactly to its original
form from the beginning (full revival). The quantum wave function periodic in time exhibits therefore the full revival
every Period (physics), period. The phenomenon of revivals is most readily observable for the wave functions being Trojan wave packet, well localized wave packets at the beginning of the time evolution for example in the hydrogen atom. For Hydrogen, the fractional revivals show up
as multiple angular Gaussian bumps around the circle drawn by the radial maximum of leading Hydrogen atom, circular state component (that with the highest amplitude in the eigenstate expansion) of the
original localized state and the full revival as the original Gaussian.
The full revivals are exact for the infinite quantum well, quantum harmonic oscillator, harmonic oscillator or the hydrogen atom, while for shorter times are approximate
for the hydrogen atom and a lot of quantum systems.
The plot of collapses and revivals of quantum oscillations of the JCM atomic inversion.
In quantum mechanics, the quantum revival
is a periodic recurrence of the quantum wave function
from its original form during the time evolution either many times in space as the multiple scaled fractions
in the form of the initial wave function (fractional revival) or approximately or exactly to its original
form from the beginning (full revival). The quantum wave function periodic in time exhibits therefore the full revival
every Period (physics), period. The phenomenon of revivals is most readily observable for the wave functions being Trojan wave packet, well localized wave packets at the beginning of the time evolution for example in the hydrogen atom. For Hydrogen, the fractional revivals show up
as multiple angular Gaussian bumps around the circle drawn by the radial maximum of leading Hydrogen atom, circular state component (that with the highest amplitude in the eigenstate expansion) of the
original localized state and the full revival as the original Gaussian.
The full revivals are exact for the infinite quantum well, quantum harmonic oscillator, harmonic oscillator or the hydrogen atom, while for shorter times are approximate
for the hydrogen atom and a lot of quantum systems.
The plot of collapses and revivals of quantum oscillations of the JCM atomic inversion.
Example - arbitrary truncated wave function of the quantum system with rational energies
Consider a quantum system with the energies and the eigenstates : and let the energies be the rational number, rational fractions of some constant : (for example for hydrogen atom , , . Then the truncated (till of states) solution of the time dependent Schrödinger equation is : .
Let be to lowest common multiple of all and greatest common divisor of all
then for each the is an integer, for each the is an integer, is the full multiple of angle and
:
after the full revival time time
:.
For the quantum system as small as Hydrogen and as small as 100 it may take quadrillions of years till it will fully revive. Especially once created by fields the Trojan wave packet in a
hydrogen atom exists without any external fields
Stroboscopic effect, stroboscopically and eternally repeating itself
after sweeping almost the whole hypercube of quantum phases exactly every full revival time.
The striking consequence is that no finite-bit computer can propagate the numerical wave function accurately for the arbitrarily long
time. If the processor number is n-bit long floating point number then the number can be stored by the computer only with the finite accuracy after the comma and the energy is (up to 8 digits after the comma) for example 2.34576893 = 234576893/100000000 and as the finite fraction it
is exactly rational and the full revival occurs for any wave function of any quantum system after the time which is its maximum exponent and so on that may not be true for all quantum systems or all stationary quantum systems undergo the full and exact revival numerically.
In the system with the rational energies i.e. where the quantum exact full revival exists its existence immediately proves the quantum Poincaré recurrence theorem and the time of the full quantum revival equals to the Poincaré recurrence time.
While the rational numbers are dense set, dense in real numbers and the arbitrary function of
the quantum number can be approximated arbitrarily exactly with Padé approximants with the
coefficients of arbitrary decimal precision for the arbitrarily long time each quantum system therefore revives
almost exactly. It also means that the Poincaré recurrence and the full revival is mathematically the same thing and it is
commonly accepted that the recurrence is called the full revival if it occurs after the reasonable and physically measurable time
that is possible to be detected by the realistic apparatus and this happens due to a very special energy spectrum having a large basic energy
spacing gap of which the energies are arbitrary (not necessarily harmonic) multiples.
.
Let be to lowest common multiple of all and greatest common divisor of all
then for each the is an integer, for each the is an integer, is the full multiple of angle and
:
after the full revival time time
:.
For the quantum system as small as Hydrogen and as small as 100 it may take quadrillions of years till it will fully revive. Especially once created by fields the Trojan wave packet in a
hydrogen atom exists without any external fields
Stroboscopic effect, stroboscopically and eternally repeating itself
after sweeping almost the whole hypercube of quantum phases exactly every full revival time.
The striking consequence is that no finite-bit computer can propagate the numerical wave function accurately for the arbitrarily long
time. If the processor number is n-bit long floating point number then the number can be stored by the computer only with the finite accuracy after the comma and the energy is (up to 8 digits after the comma) for example 2.34576893 = 234576893/100000000 and as the finite fraction it
is exactly rational and the full revival occurs for any wave function of any quantum system after the time which is its maximum exponent and so on that may not be true for all quantum systems or all stationary quantum systems undergo the full and exact revival numerically.
In the system with the rational energies i.e. where the quantum exact full revival exists its existence immediately proves the quantum Poincaré recurrence theorem and the time of the full quantum revival equals to the Poincaré recurrence time.
While the rational numbers are dense set, dense in real numbers and the arbitrary function of
the quantum number can be approximated arbitrarily exactly with Padé approximants with the
coefficients of arbitrary decimal precision for the arbitrarily long time each quantum system therefore revives
almost exactly. It also means that the Poincaré recurrence and the full revival is mathematically the same thing and it is
commonly accepted that the recurrence is called the full revival if it occurs after the reasonable and physically measurable time
that is possible to be detected by the realistic apparatus and this happens due to a very special energy spectrum having a large basic energy
spacing gap of which the energies are arbitrary (not necessarily harmonic) multiples.
See also
* Poincaré recurrence theoremReferences
{{Reflist Quantum mechanics Quantum chaos theory